今回は立体図形のうち,回転体の問題に焦点をあて解説していきます。回転体の問題とは以下で紹介するような,平面で提示された図形をある軸に沿って回転させ,そうしてできた立体の体積を求めるものです。
このような問題では平面上での図形の把握・空間上での図形の把握,という2通りの視点が必要とされ,またそれらのイメージをつなぎ合わせるという点で高度なテクニックが求められます。しかし慣れてしまえば他の受験生に差をつける得点源になること間違いなしです。本記事に載っている例題を解きながら,回転体をマスターしてしまいましょう!
Contents
攻略法を例題つきで解説
ここからは実際に回転体の面積を求めていく練習をしていきましょう。使用するのは次の問題です。入試問題からの引用ですが,少し簡単にアレンジしています。よろしければまずはご自身の力だけで答えにたどり着けるか,挑戦してみてください。
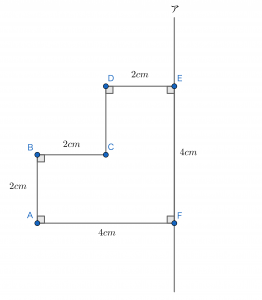
次の図形を直線アの周りに1回転させたときにできる立体の体積を求めなさい。ただし,円周率は3.14とします(神奈川学園中学校(2019),一部改題)
いかがでしょうか。解けた方もそうでない方も,途中までなら出来たという方もいらしたかもしれません。ここからはこの問題を活用しつつ,回転体の問題を解くときのポイントを学習していきましょう。
解答の手順①
回転体の問題では3つの段階を踏む必要があります。まずは回転体の名の通り,回転することをイメージしなければなりません。当たり前と言えば当たり前ですが,点と線分という平面上の情報を空間上に落とし込み,出来上がる図形の大まかな形を把握しておくことは非常に重要です。
ではどのようにすれば空間への落とし込みが達成できるのでしょうか。そのコツは点の軌跡を想像することにあります。
点の軌跡とは点が回転するときに通る道筋のことを指します。今回は軸アを中心にして図形が回転するわけですから,図形の一部である点は円を描くように動くわけです。上の図形で言うならば,点A〜点Fは次のように動きます。
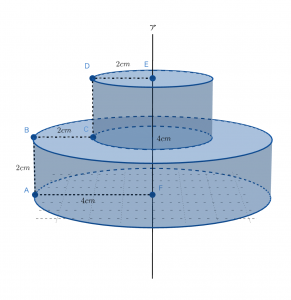
元の図形は点線で表されています。きれいな回転体が出来ましたね。このように点が円を描いて運動することを意識すると上手く立体を作れます。
このときに重要なのは円の軌道を潰して図示することと奥にあるものを点線で描くことです。立体を想像するとは言っても,それを表すのはあくまで平面上です。したがって空間上に存在するように工夫して平面に描かなければなりません。この2つを守ることで一段と立体を理解しやすくなるでしょう。
この辺りのテクニックは慣れるうちに身につくものでもある上に,平面に表さないと解けないと言うわけではありませんが,図形の把握においては大事な技術となります。受験に臨むにあたって覚えておきたいものです。
解答の手順②
次に表した空間上の回転体を,体積が求められるように分割することです。基本的には回転体はいくつかの円柱の組み合わせでできていて,そのまま体積が求められることはほとんどありません。すなわち上で見た回転体を円柱という部分に切断していきましょう。ここでのコツは内側にくぼんでいるところに注目することです。今回では点Cの周辺が相当します。
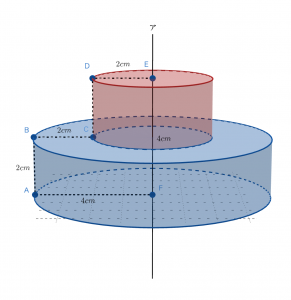
点Cの辺りに注目すると,上のように線分BCを含む平面で,赤い小さな円柱と青い大きな円柱の2つに図形が分けられますね。この問題は比較的簡単であったため,先の図で2つの円柱の組み合わせだ!と分かった方もいたかもしれませんが,特に難易度の高い問題では図形のくぼみに焦点を当てるということは大事です。なぜならそこが立体の切断面になっている可能性が高いからです。
解答の手順③
ここまでくれば後は分割した円柱の体積をそれぞれ求め,それらを足し合わせれば答えが導き出せそうです。計算ミスに気をつけて計算を進めていきましょう。
まずは赤い部分の体積を求めていきます。この円柱の半径は2cm,高さも2cmであり,円周率は問題文で言われている通り3.14です。このことから小さい円柱の体積は2×2×3.14×2=25.12(cm3)であると計算できます。
次に青い部分の体積を算出していきます。この円柱の半径は4cm,高さは2cmであり,円周率は上と同じく3.14であるため,体積は4×4×3.14×2=100.48(cm3)であると求められました。
したがって回転体全体の体積は赤く小さい円柱と青く大きな円柱の和で求められるため,その値は25.12+100.48=125.6(cm3)となりました。これで答えを無事導くことができましたね。
解答の手順まとめ
以上が回転体の問題を解くテクニックとなります。改めて確認しておくと,回転→分割→計算という手順を踏むとこのような問題は解きやすくなります。今回引用した例題は標準的な難易度のものでしたが,基本的な流れはどんな問題でも変わりません。本記事では引き続き2つの問題を引用します。これらは少し難しいですが,今回お伝えした解き方を利用して挑戦してみましょう。
練習問題に挑戦①
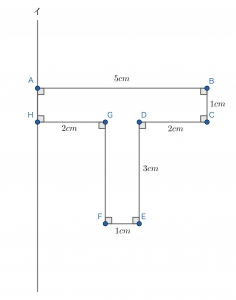
次の図形を直線イの周りに1回転させたときにできる立体の体積を求めなさい。ただし,円周率は3.14とします(帝京大学中学校(2017),一部改題)
解説
それではここからは上の問題の解説をしていきます。最初の例題に比べると1点難しいポイントが存在するため,その部分は特に重点的に取り扱います。
まずは直線イを軸に回転させたときの立体について考えます。手順通り回転させた図形をイメージしていくと,次のような図形が空間上に表されます。

元の図形を点線で,立体を青色で表しています。本問で重要なのは,先程の例題と違ってくり抜かれたような部分があることです。灰色で表されている部分がそのくり抜かれた場所なのですが,この部分の体積は取り除かなければなりません。
このくり抜かれた部分の有無を見分けるポイントは,回転する図形の縦に伸びる線分が軸に触れているかどうかです。今回は線分AHが軸イと触れていますが,線分GFは軸とは触れず,2cmのスキマが生まれています。そのため点H・点G・点Fが回転するときにくり抜かれた立体が出てきてしまうのです。このことを念頭に置いて以降の計算を進めましょう。
次に図形を分割します。上の図からもお分かりでしょうが,今回の図形は点Gの辺りでくぼんでいるため,そこに注目すると次のように分割できます。
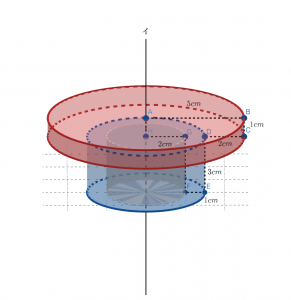
立体は赤く平べったい部分と青い縦長の部分に分けられました。これらの部分と前述した灰色のくり抜かれた部分を計算することで,回転体の体積を算出できそうです。
これらのことを基にそれぞれの部分の体積を求めます。まず赤い部分ですが,この円柱の半径は5cm,高さは1cmであり,円周率は3.14です。よってその体積は5×5×3.14×1=78.5(cm3)となります。
次に青い部分ですが,この立体は半径3cm・高さ3cmの円柱です。上と同様に計算すると体積は3×3×3.14×3=84.78(cm3)となります。
最後に灰色のくり抜かれた部分の体積を計算しましょう。この部分は半径2cm・高さ3cmの円柱であるため,体積の値は2×2×3.14×3=37.68(cm3)です。
以上のことから回転体の体積は78.5+84.78-37.68=125.6(cm3)となるため,答えは125.6cm3です。
問題(2)
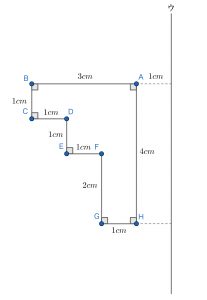
次の図形を直線ウの周りに1回転させたときにできる立体の体積を求めなさい。ただし,円周率は3.14とします(明治大学附属中野中学校(2018),一部改題)
解説
ここからは①同様に問題の解説を行います。
まずは直線イを軸に回転させたときの立体について考えます。手順通り回転させた図形をイメージしていくと,次のような図形が空間上に表されます。
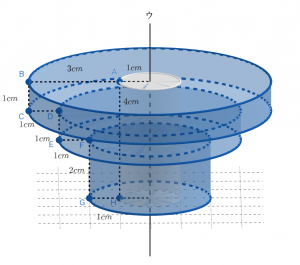
点線が元の図形,青い立体が出来上がる回転体を指しています。また真ん中に灰色のくり抜かれた部分が存在することもわかります。これは線分AH が軸ウと触れず,1cmのスキマができているからですね。①で抑えたポイントを活用していきましょう。
そしてこの立体を分割すると,以下の図のように3つに分けることができます。
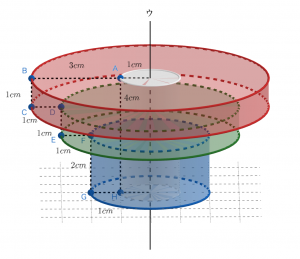
上から順に赤い円柱・緑の円柱・青い円柱の3つに分けられました。これも上で見たテクニックの通り,点D・点Fというくぼみに注目するときれいに3つに分割できます。つまりこの回転体は,赤い円柱・緑の円柱・青い円柱の体積を足し,そこから灰色のくり抜かれた部分の体積を引くことで,その体積が求められると想定されます。
したがって順番に体積の値を求めましょう。赤い円柱の半径は4cm・高さは1cmであるためその体積は4×4×3.14×1=50.24(cm3),緑の円柱の半径は3cm・高さは1cmなので体積は3×3×3.14×1=28.26(cm3),青い円柱の半径は2cm・高さも2cmなので体積は2×2×3.14×2=25.12(cm3)となります。
次にくり抜かれた立体の体積を計算します。この円柱の半径は1cm・高さは4cmなので,体積は1×1×3.14×4=12.56(cm3)と求められます。
これらのことから最終的な回転体の体積を算出すると,50.24+28.26+25.12-12.56=91.06(cm3)になります。よって答えは91.06cm3です。
まとめ
今回は回転体の問題を解くテクニックをご紹介し,その解き方を2つの問題を活用しながらマスターする,と言った内容でした。回転体の攻略法はもう完璧に覚えられましたか?ここでまとめとして改めて解くときの流れやポイントを復習しておきましょう。
- 初めに点が円を描くことをイメージすると回転体が想像しやすい!
- 回転体を図示するときは円を潰し,奥にあるものを点線で描くと分かりやすい!
- 回転体はいくつかの円柱の組み合わせでできており,その切断面を知るには図形のくぼみを見ると分かりやすい!
- 軸と線分のスキマからくり抜かれた部分を特定しよう!
ここで確認したテクニックは回転体の問題でしか使えない,というわけではありません。他の空間図形の範囲でも応用できるでしょう。色々な問題にチャレンジしていく中で,参考にしていただければ幸いです。
(ライター:大舘)