今回のテーマは,平面図形と比の問題です。この範囲は広いですし,様々な形の図形問題が出て混乱してしまう人もいるのではないでしょうか。嫌になってしまう人もいることかと思います。そこで今回は,まずはじめに押さえておきたい部分,絶対に覚えておいて欲しい,という基本的なところをご紹介します。是非この機会に図形問題の基本を押さえて,得意分野にしてしまいましょう!
Contents
三角形の辺の比と面積の比
面積比と底辺比の関係
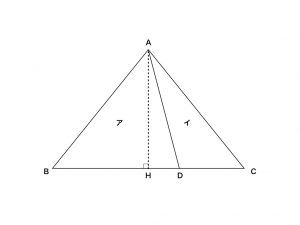 [図1]
[図1]
まずはじめに押さえてほしいポイントは,高さが等しい三角形の面積の比は,底辺の長さの比と等しいことです。
図1を見てみましょう。三角形ABDをア,三角形ADCをイとします。アとイの高さはどちらもAHですね。三角形アとイの面積の比は,
\((三角形アの面積):(三角形イの面積)=(BD\times AH\div 2):(DC\times AH\div 2)\)
\(=BD:DC\)
これで三角形の面積の比と,底辺の長さの比が等しいことがわかりましたね。
面積比と辺の比の関係
次に押さえてほしいポイントは,ある角が等しいとき,その角を作る2辺の比をかけた値の比が面積比になるということです。言葉だけでは少しわかりづらいので,具体的に見ていきましょう。
図1で,三角形ABCと,三角形アの面積比を考えると,
\((三角形ABCの面積):(三角形アの面積)=(AB\times BC):(AB\times BD)\)
になります。この場合は,ABが共通しているため,結局BC:BDとなり,先ほどの底辺比ともかぶりますね。
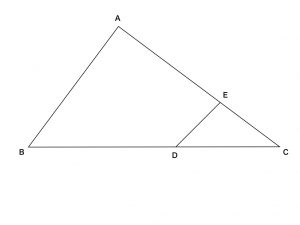 [ 図2]
[ 図2]
また図2のような,三角形ABCと三角形CDEの面積比を考えると,
\((三角形ABC):(三角形CDE)=(AC\times BC):(CE\times CD)\)
になります。
合同条件と相似条件
合同と相似,平面図形の範囲ではよく耳にする言葉かと思います。では具体的に,どのような状態のことを合同や相似というか,ちゃんと把握できていますか?
2つの三角形が同じ形かつ同じ大きさであるとき,2つの三角形は合同であるといいます。ぴったり重ね合わせられる状態のことですね。また,2つの三角形が同じ形だけど大きさが異なるとき,2つの三角形は相似であるといいます。タブレットを使うとき,2本指でズームするとき,大きさは変わりますが形は変わりませんよね。このときのズーム前とズーム後の図形は,相似です。
合同か相似かを判断するための条件が存在します。
【三角形の合同条件】
- 3辺がそれぞれ等しい。
- 2辺とその間の角がそれぞれ等しい。
- 1辺とその両端の角がそれぞれ等しい。
【三角形の相似条件】
- 3組の辺の比が全て等しい。
- 2組の辺の比とその間の角がそれぞれ等しい。
- 2組の角がそれぞれ等しい。
上の相似条件からもわかるように,2つの相似な三角形では,対応する3つの辺の長さの比は等しくなっています。このときの辺の長さの比を相似比といいます。
相似な図形の面積比について考えてみましょう。例えば,三角形Aと三角形Bの相似比がa:b のとき,底辺の比と高さの比はどちらもa:b なので,
\((三角形Aの面積):(三角形Bの面積)=(a\times a\div 2):(b\times b\div 2)\)
\(=(a\times a):(b\times b)\)
になります。
主な相似の例
【ピラミッド型の相似】
 [図3]
[図3]
図3を見てください。辺ABと辺CDが平行で,●どうしの角,×どうしの角は,それぞれ同位角で等しいので,三角形OABと三角形OCDは相似です。相似比は,
\(AB:CD=OA:OC=OB:OD\)
となります。
よくある間違いで,OC:CA=CD:ABとしてしまう人がいますが,これは相似比ではありません。 OC:CA=OD:DB は成り立ちますが,間違えやすいので相似比の問題では,できるだけOC:OAで見るようにしましょう。ミスを減らすためにも,三角形OABと三角形OCDが相似であるというポイントを押さえて,どの辺が対応しているのかを理解しておきましょう。
【クロス型の相似】
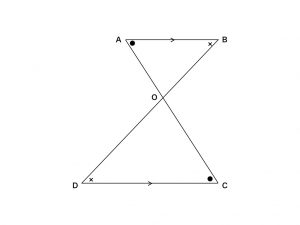
[図4]
図4を見てください。辺ABと辺CDが平行で,●どうしの角,×どうしの角は,それぞれ錯覚で等しいので,三角形OABと三角形OCDは相似です。相似比は,
\(AB:CD=AO:OC=BO:OD\)
となります。
【例題1】
- 問題
- (1) 次の図において,三角形ABCと三角形DEFは相似である。相似比を求めなさい。また,辺BCの長さは何cmですか。
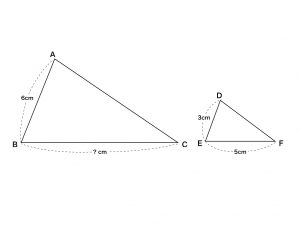
-
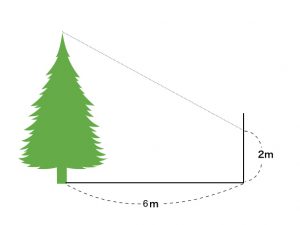
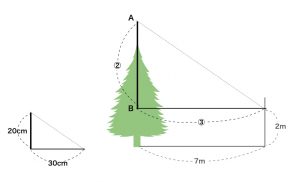
- (2) へいから6mのところに木が立っていて,木の影が右図のように映っています。また,同じ時刻に,長さ20cmの棒の影の長さが30cmありました。この木の高さは何mですか。
- 【解説】
- (1) 三角形ABCと三角形DEFの相似比は, 6:3=2:1
また,辺BCの長さは, 6:3=?:5 より,10cm - (2) まず,棒の影と木の影が映るようすを表します。太陽の光は平行なので,木の影の先端から地面に平行な線を引きます。すると,棒の影の三角形と,木の影の三角形は相似な図形になります。
よって,(棒の長さ):(棒の影の長さ)=(木の高さ):(木の影の長さ) となるので,20:30 = 2:3
次に,ABの高さは, \( 6 \times \frac{2}{3} = 4 \)
よって,木の高さは, 2 + 4 = 6m
- (1) 三角形ABCと三角形DEFの相似比は, 6:3=2:1
円とおうぎ形
円周の一部のことを弧といい,円の2つの半径とその間の円弧によって囲まれた図形をおうぎ形といいます。図5では色のついた部分です。円の中心部分の,おうぎ形の角を中心角といいます。中心角が180度のおうぎ形は半円,中心角が90度のおうぎ形を四分円といいます。
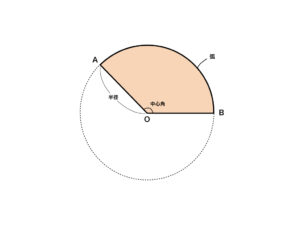 [図5]
[図5]
また,直径に対する円周の割合を円周率(多くの場合は近似値の3.14を用います)といいます。これはどの大きさの円でも一定で,およそ3.14です。円周の長さは次のようになります。
- \([円周の長さ]=[直径]\times [円周率]\)
- \([円弧の長さ]=[円周]\times \frac{中心角^\circ}{360^\circ}\)
円の面積の公式もここでご紹介します。
- \([円の面積]=[半径]\times [半径]\times [円周率]\)
- \([おうぎ形の面積]=[円の面積]\times \frac{中心角^\circ}{360^\circ}\)
【例題 2】
- 問題
次の問いに答えなさい。だたし,円周率は3.14とします。- (1) 直径が4 cmの円の円周の長さは何cmですか。
- (2) 半径が3 cm,中心角が 120度のおうぎ形の弧の長さは何cmですか。
- (3) 半径が2 cmの円の面積は何㎠ですか。
- (4) 半径が6 cm,中心角が 120度のおうぎ形の面積は何㎠ですか。
- 【解説】
- (1) \(4\times 3.14=12.56\)(cm)
- (2) \( 3 \times 2 \times 3.14 \times \frac{120^\circ}{360^\circ} = 6.28 \) (cm)
*問題文で与えられているのは半径なので,直径にして計算するのを忘れないようにしましょう。 - (3) \(2\times 2\times 3.14=12.56\)(cm2)
- (4) \( 6 \times 6 \times 3.14 \times \frac{120^\circ}{360^\circ} = 37.68 \)(cm2)
終わりに
いかがでしたか?今回は平面図形と比の絶対に押さえておきたい基本的な部分をご紹介しました。平面図形と比に関しての問題は解けるようになったでしょうか。今回ご紹介した基本を押さえたら,あとは問題をたくさん解いて慣れていくだけです。様々な形で出題される図形に慣れていきましょう!この分野についての理解が少しでも深まり,苦手意識が薄れた方がいたら私も嬉しいです。頑張ってください!















