問題
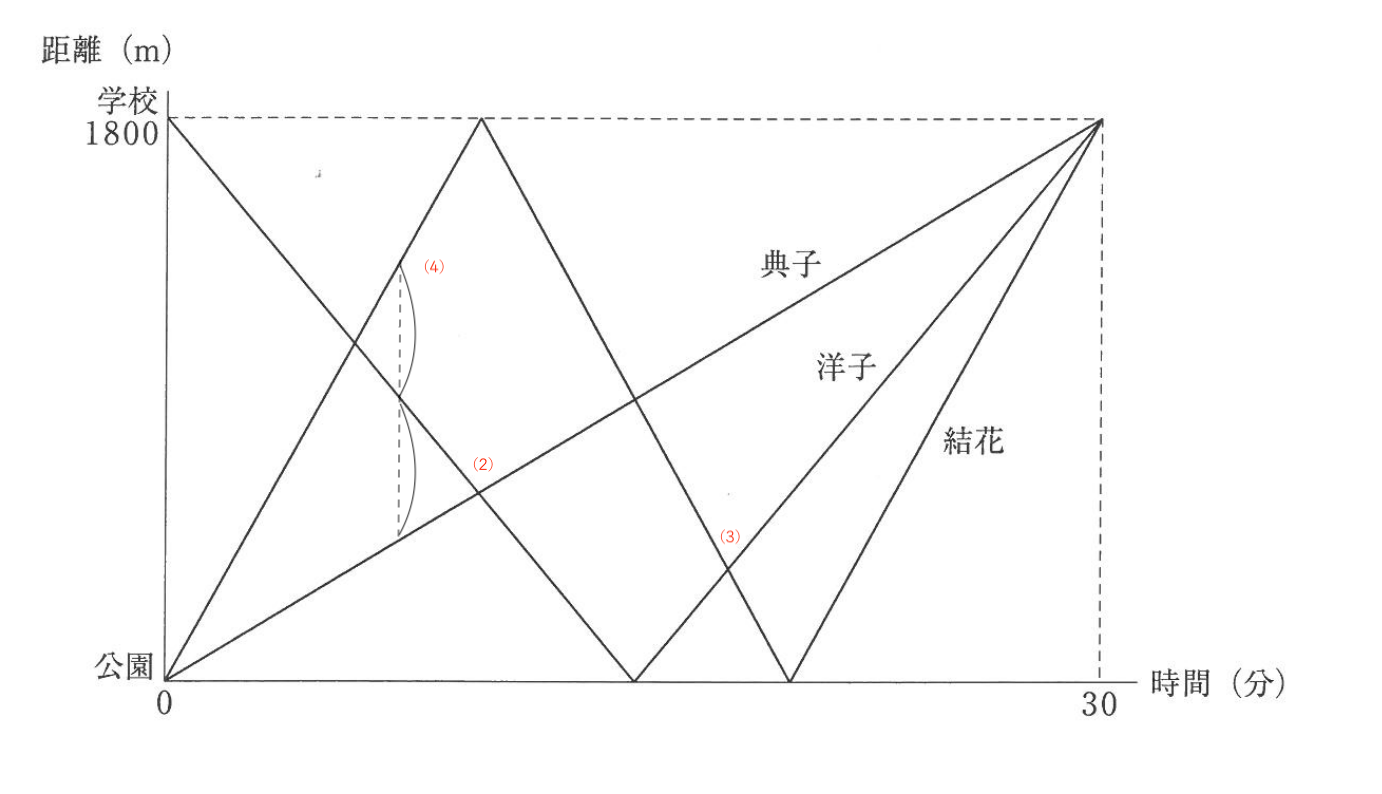
1800m離れた公園と学校の間を、典子さんは歩き、洋子さんは走り、結花さんは自転車に乗って移動しています。3人は公園または学校を同時に出発し、30分後に全員学校に到着しました。下のグラフは、3人の移動の様子をグラフに表したものです。次の問いに答えなさい。ただし、3人の進む速さはそれぞれ一定とします。
- (1)典子さんの歩く速さは分速何mですか。
- (2)典子さんと洋子さんがはじめて会ったのは、出発してから何分後ですか。
- (3)洋子さんと結花さんが2回目に出会うのは、公園から何mのところですか。
- (4)典子さんと洋子さん、洋子さんと結花さんの間の距離が初めて等しくなるのは、出発してから何分何秒後ですか。

解説
全体と通して言えることですが、人名が非常に紛らわしいので、各設問で誰を基準に考えているのかを間違えないようにしましょう。(私も、解説を作りながら何度かミスりました…)
(1)単純な速度の計算
典子さんは1800mを30分で移動していますから、
\(1800 \div 30=60\)
より、分速60mとわかります。
答え:分速60m
(2)出会い算
まずは、洋子さんの走る速さを求めると、
\(1800 \times 2 \div 30=120\)
より、分速120mとわかります。
2人が出会うのは、上の図の(2)のところなので、
1800mの距離を、典子さんは分速60m、洋子さんは分速120mで近づいていくので、
\(1800 \div (60+120)=10\)
より、10分後に出会うことがわかります。
答え:10分
(3)少し複雑な出会い算
まずは、結花さんの移動速度を求めると、
\(1800 \times 3 \div 30=180\)
より、分速180mとわかります。
2人が2回目に出会うのは上の図の(3)のところなので、出会った時間を、出発から□分後とすると、
\(2人が移動した距離=120 \times □+180 \times □\)
\(1800 \times 3=300 \times □\)
\(□=5400 \div 300\)
\(=18\)
より、18分後とわかります。
また、洋子さんが初めて公園に到着するのが、出発から15分後で、その3分後に結花さんと出会うので、
\(3 \times 120=360\)
より、2人が出会った場所は公園から360m離れたところになります。
答え:360m
(4)速さと比の複合問題
3人の間の距離が等しくなるという状況は、結花さんと洋子さんがはじめに出会うまでは、生じ得ないので、結花さんと洋子さんがはじめに出会った後を考えていきます。
そうすると、上の図の(4)のところで等しくなりそう(目分量なのであくまで推測です)なので、それまでに経過した時間を△分とすると、
典子さんの移動距離が、
\(60 \times △\)
洋子さんの移動距離が、
\(120 \times △\)
結花さんの移動距離が、
\(180 \times △\)
となり、典子さんと洋子さんの間の距離と洋子さんと結花さんの間の距離の合計を考えると、
\(180 \times △-60 \times △=120 \times △\)
となり、両者の間の距離は等しいから、1つ分の距離は、
\(120 \times △ \div 2=60 \times △\)
と表すことができます。
ここで、公園から学校までの距離を△を用いて表すと、
\(1800=60 \times △+60 \times △+120 \times △\)
\(=240 \times △\)
\(△=1800 \div 240\)
\(=7.5\)
となり、7.5分後に両者の距離が等しくなるとわかります。
答え:7分30秒
おすすめ記事
- 夏期講習までに押さえておくべき算数の基礎 その2 速さ
- 往復の平均の速さ、間違えずに求められますか?
- 「旅人算」の解き方を問題で学ぼう![出会い・追いかけ・3人旅人算]
- グラフが登場する旅人算の解き方を問題集形式でご紹介!
- 「流水算」でつまずかない考え方とは?解き方が身につく練習問題付き!