旅人算の基本！図をかいて整理しよう

中学受験において「速さ」に関する問題は必ずと言ってよいほど出題されます。

速さに関する問題には、「速さの三用法」「旅人算」「点の移動」「ダイヤグラム」「通過算」「流水算」「時計算」など、実に様々なパターンがあります。

今回は、その中でも最も定番の「旅人算」の基本の考え方について説明していきます。「出会い」「追いかけ」の基本問題と、「3人旅人算」の典型題をご紹介しています。

（なお、「はじき」「みはじ」などは使わなくてよいと思っているので、この記事の中ではこれらの使い方は説明していません）

Contents

1 速さの基本の考え方
2 旅人算の基本パターン
3 進行方向だけで判断してはいけない
4 3人旅人算の典型題
5 続きは…【練習用プリントあり】
6 おすすめ記事
7 参考

速さの基本の考え方

「速さ」とは「一定時間あたりに進む長さ」になります。速さの単位については、次のような言葉で表します。

1秒あたりに進む長さ＝秒速、毎秒
1分あたりに進む長さ＝分速、毎分
1時間あたりに進む長さ＝時速、毎時

例えば1秒あたりに2m進む人の速さは「秒速(毎秒)2ｍ」です。これを1分あたりに換算すると、2×60＝120(ｍ)進むことになるので、「分速(毎分)120ｍ」となります。

さらに1時間あたりに換算すると、120×60＝7200(ｍ)、つまり7.2㎞進むことになるので、「時速(毎時)7.2㎞」となります。特に規定があるわけでもありませんが、時速に直すと距離が長くなるので「㎞」に直すことが多くなります。

速さの三用法の公式については、「速さ×時間＝距離」だけ覚えておけばよいです。速さや時間を聞かれた場合には逆算すればすむことになります。

また、公式は覚えていなくても言葉の意味から考えればどのような計算をすべきかがわかるはずなので、公式に頼るよりはしっかりと文章を読むようにしてください。

旅人算の基本パターン

速さの問題の中で、「登場人物が複数いる問題」を「旅人算」と呼びます。登場人物が複数いることによって何が起こるかというと、「出会い」や「追いかけ」といったパターンの問題が生まれます。

最も王道なのは登場人物が2人の場合で、2人の速さの「和」か「差」に注目して解く、というのが旅人算の基本パターンです。登場人物が3人や4人になったときも、2人ずつ考えていくことで解法の糸口を見つけ出せます。

出会いの基本

離れた2地点から向かい合って進んでいった場合に、時間が経てば「出会う」というイベントが発生します。

このとき、2人の速さと、出発してから出会うまでの時間や進んだ距離などの進行状況を考えていきます。実際に問題を解きながら考えていきましょう。

問題

ＡくんとＢくんが3㎞はなれた地点から向かい合って同時に出発しました。Ａくんは毎分30ｍ、Ｂくんは毎分70ｍで歩いたとすると、2人が出会うのは出発してから何分後ですか。

【考え方】1分間に、30＋70＝100(ｍ)ずつ近づいていく。

【解説】3㎞＝3000ｍ、3000÷(30＋70)＝30(分)より、30分後に出会います。

2人の進んだ長さの和が3㎞(＝3000ｍ)になったときに「出会う」というイベントが発生します。1分間に100mずつ近づいていることを考えれば、公式に頼らずとも自然と「3000÷100」という式が出てきますね。

ちなみに、出会ったあとは離れていくのですが、その場合にも「1分間に100mずつ離れていく」ということになります。

追いかけ

離れた2地点から同じ方向に進んでいる場合に、「追いかけ」というイベントが発生します。後ろから追いかけている人の方が速くないと、当然のことながら追いつけません。

このとき、2人の速さと出発してから追いつくまでの時間や進んだ距離といった進行状況を考えていきます。ぜひ問題を解きながら考えてみてください。

問題

1㎞先を毎分30ｍの速さで歩いているＡくんを、Ｂくんが毎分70ｍの速さで追いかけます。ＢくんがＡくんに追いつくのはＢくんが出発してから何分後ですか。

【考え方】1分間に、70－30＝40(ｍ)ずつ近づいていく。

【解説】1㎞＝1000ｍ、1000÷(70－30)＝25(分)より、25分後に追いつきます。

最初の1㎞(＝1000ｍ)の距離の差を縮めたときに、「追いつく」というイベントが発生します。1分間に40ｍずつ追いついているので、「1000÷40」という式になりますね。

ちなみに、追いついたあとは「追い越してどんどん離れていく」ということになりますが、その場合にも1分間に40ｍずつ離れていくことになります。

池のまわりをまわる問題

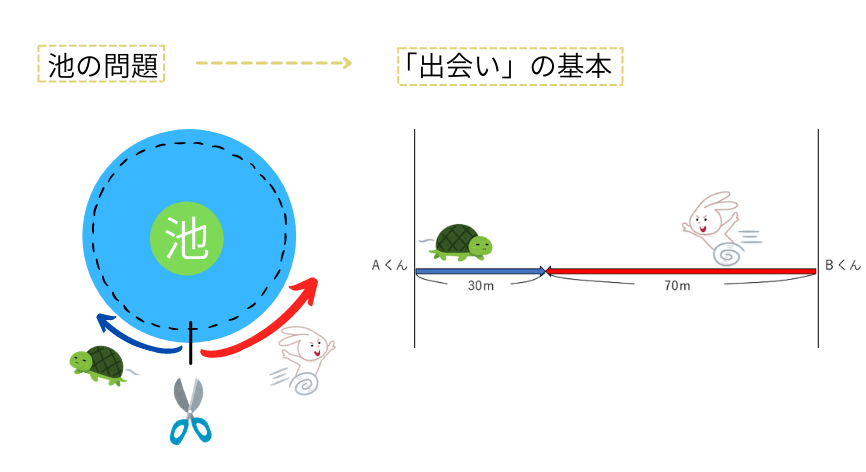
池の周りをまわる問題でも同じような問題が出題されることがあります。

池の周りの同じ地点から出発して反対方向に進んでいる場合には、池をスタート地点の所からプチっと切って伸ばすと出会いの基本と同じ図になりますので、同じようにして考えることができます。

「状況が変わっても同じように考えられないか」を試してみるとわかりやすくなるので、色々な問題で練習してみてください。

進行方向だけで判断してはいけない

旅人算のごくごく基本の問題だけを取り組んでいると、「同じ方向に進むときは速さの差、反対方向に進むときは速さの和」というような間違った覚え方をしてしまう人がいます。こういった思い込みによって、解けない問題が出てきてしまうので気をつけてもらいたいところです。

旅人算の問題は、実に多様な問題を用意することができます。出発の時間が異なる問題や、途中で速さや進行方向が変わるといった問題も割と定番です。

全ての問題を紹介していくと問題集が出来上がるので、今回はちょっとだけご紹介します。

問題

ＡくんとＢくんがＰ地点を同時に出発し、Ｐ地点から2.4㎞はなれたところにあるＱ地点へ向かいました。Ａくんは毎分30ｍ、Ｂくんは毎分70ｍで歩き、Ｑ地点に着いたらそのまま休まずに引き返します。2人が初めてすれちがうのは、出発してから何分後ですか。

【考え方】図で考えると、差ではなく和が求められる。Bくんが引き返してきてから出会うので、2人の進んだ距離の和が、2.4×2＝4.8(㎞)となる。

【解説】4.8㎞＝4800ｍ、4800÷(30＋70)＝48(分)より、48分後にすれちがいます。

上の問題のように、同じ地点から出発している問題でも、出会いのパターンになることがあり得ます。「同じ方向に進むんだから、差で考えるんでしょ？」という間違った思い込みがあると、この問題はなかなか解けません。

旅人算の問題は、「2人の和」か「2人の差」が解くためのカギになります。どちらが求められるのかは問題文の状況次第となるので、問題文をよく読んで条件を整理しながら考えていきましょう。

3人旅人算の典型題

旅人算の問題の中で、登場人物が2人でなく3人や4人になる場合があります。登場人物が3人の旅人算を「3人旅人算」と呼んでいます。

この3人旅人算の中で、一番よく出題されているであろう問題が次のような問題です。

問題

1本の道にそってＰ地点とＱ地点があります。Ｐ地点から春子と秋子が、Ｑ地点から夏夫が同時に出発し、向かい合って進みました。春子と夏夫がすれちがってから5分後に、秋子と夏夫がすれちがいました。春子は毎分80ｍ、秋子は毎分60ｍ、夏夫は毎分100ｍで歩いていたとすると、Ｐ地点とＱ地点は何㎞はなれていますか。