| 中学受験ナビ【函館・横浜に系列校も！】雙葉中学校の算数の特徴とは？最新の出題傾向や入試対策方法ついてもご紹介！

雙葉中学校は、東京都千代田区六番町に所在する、中高一貫の私立女子中学校です。

完全中高一貫校であるため、高校からの募集は行っていません。

また、創立は1875年に遡り、都内女子校のなかでも歴史が長いです。

桜蔭中学校・高等学校、女子学院中学校・高等学校とともに「女子御三家」と称され、都内でもトップクラスの難易度をほこります。

今回は、そのような雙葉中学校の、算数の出題傾向や入試対策方法についてご紹介します！

入試情報

問題構成

雙葉中学校の算数は、試験時間50分に対し大問が5〜6問、総設問数が10〜15問程度となっています。

大問5〜6問のうち、第1問は基本的な四則混合の計算問題と小問集合の問題、第2問〜第6問は応用問題という問題構成です。

解答形式

雙葉中学校の算数は解答用紙が用意されておらず、問題用紙上に直接解答を記入する形式です。

問題用紙の空欄に途中式や考え方を記入し、その記述が採点対象となります。

そのため最終的な答え自体が正しくても、解答の途中過程が十分に記述されていない場合、高得点は期待できません。

しかし、問題用紙のスペースには必ずしも余裕があるとは限りません。記述や筆算などを自由に書いてしまうとスペースが足りなくなり、必要な記述が書き切れなくなってしまう危険性もあります。そのため、必要な説明や式をコンパクトに取捨選択して記述することが重要です。

近年の出題内容

2021年度

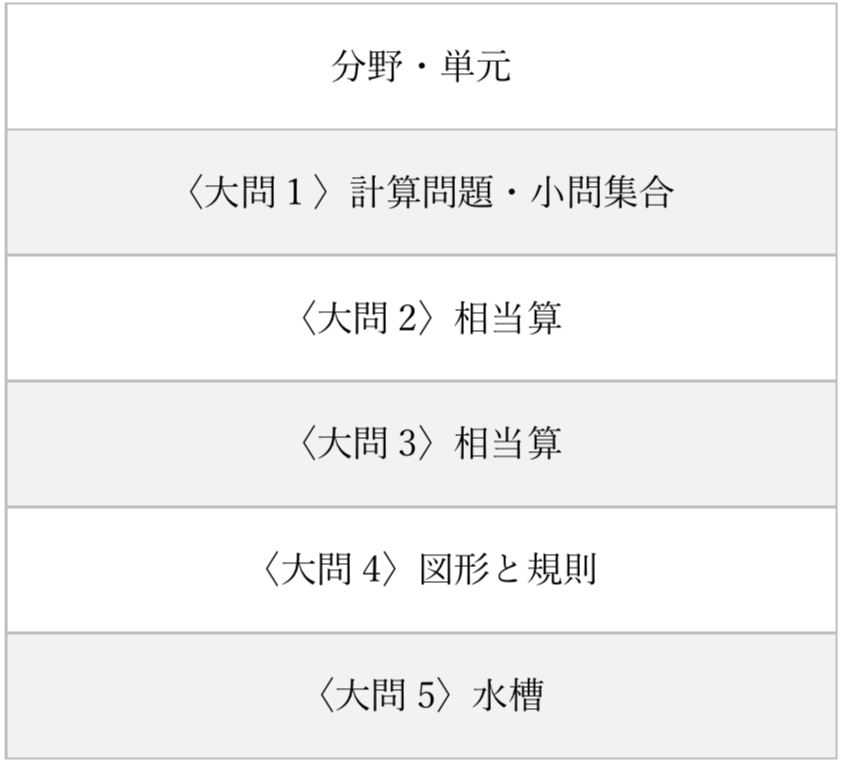
2020年度

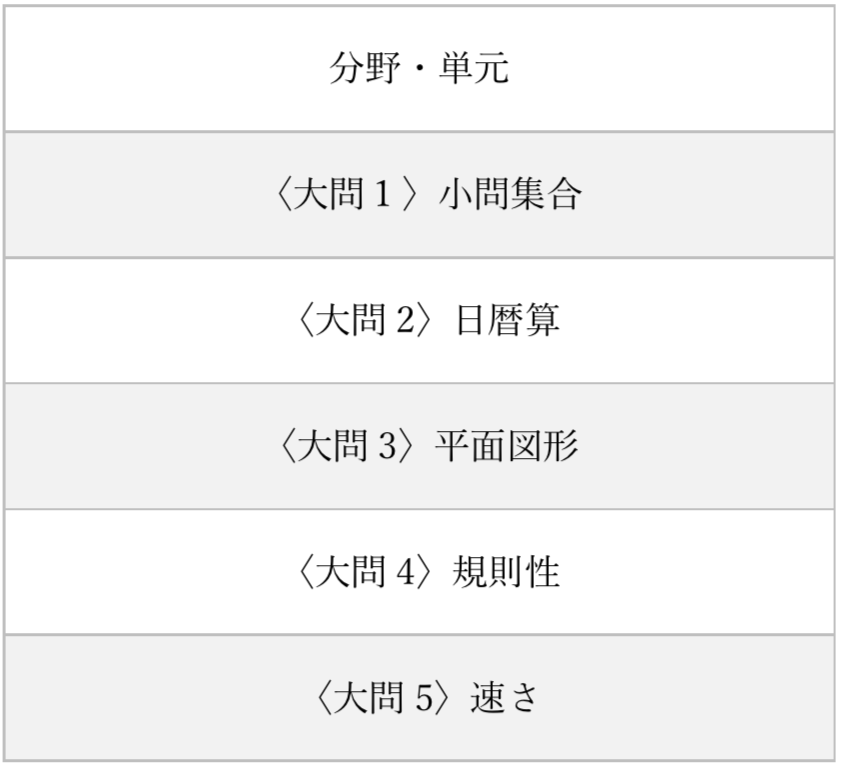
2019年度

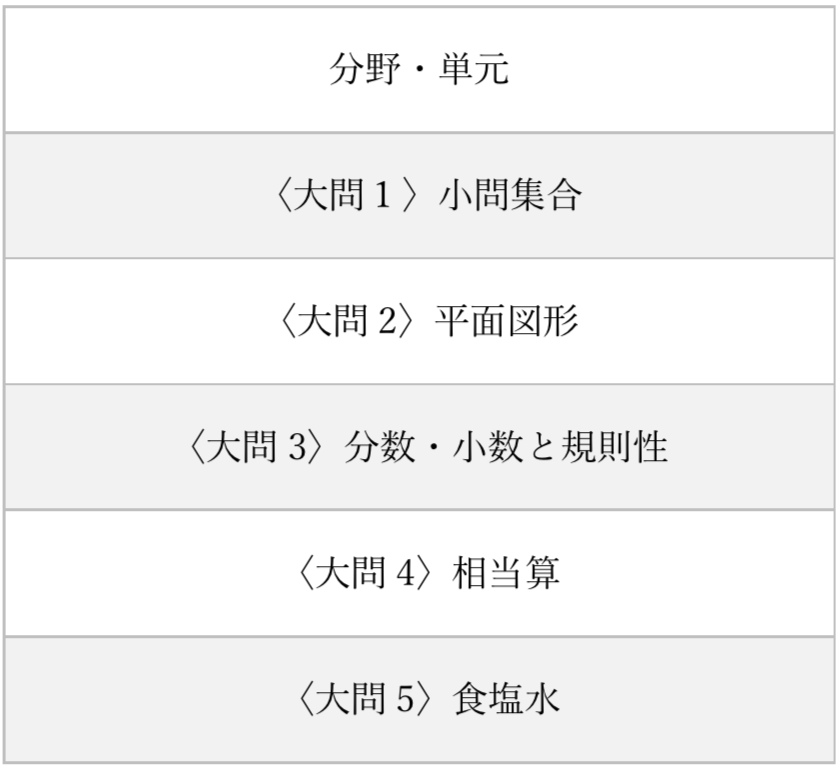
出題傾向

概要

出題傾向に偏りあり

雙葉中学校の算数は、他の難関校と比べても出題傾向に偏りがあります。

特に「多角形・おうぎ形の複合図形」、「規則性」、「和・差・比の文章題」、「速さ」の4単元が頻出で、これらの中からほぼ毎年出題されています。

複雑な計算処理を伴う問題・全体的に手間のかかる問題が多い

雙葉中学校の算数では、複雑な計算処理を必要とする問題が頻繁に出題されています。毎年計算問題が出題されているわけではなく、計算問題以外の問題で煩雑な計算を必要とする場合が多いです。

具体的には円周率(3.14)を用いた計算など、複雑な処理を必要とする少数計算や分数計算などが頻出で、計算だけでもかなり時間がかかってしまいます。

内容

出題分野・出題傾向についての詳細

【頻出分野】

計算

四則計算、逆算、計算の工夫

和と差

和差算、分配算、消去算、つるかめ算、過不足算、差集め算

割合と比

割合と比、濃度、仕事算、ニュートン算、還元算、相当算、売買損益

速さ

速さ、旅人算、通過算、流水算

図形

角度、面積、長さ、体積、表面積、構成、分割、図形・点の移動、表とグラフ

規則性

植木算、周期算、数列、方陣算、図形と規則

出題傾向・難易度についての詳細

雙葉中学校の算数は、大問５〜６問と他の学校と比べても問題数が少なく、その分１問１問が手間のかかる問題となっています。具体的には数え上げ・推理を要する問題や、円周率(3.14)・煩雑な少数分数計算が頻出です。

計算問題は、必ずしも単体で出題されているわけではなく、他の単元の問題の中で煩雑な計算処理を要することも多いです。

難関男子校で出題されるような、いわゆる難問や奇問といった高度なひらめきや思考力を必要とするような問題は少なく、その単元に関する理解を問うような問題がほとんどです。

また本校の算数は、問題用紙上に直接解答を記入する形式で、途中式や考え方についての説明も採点対象となります。

そのため、最終的な答えに辿り着かなかったとしても、途中まで考え方が適切に示されていれば途中点をもらえる可能性があります。早い時間でなるべく多くの問題をこなすというよりは、あきらめずにじっくり、慎重に解くことを意識すると良いでしょう。

また頻出の単元に偏りがあることも特徴のうちの1つです。特に、「多角形・おうぎ形の複合図形」、「規則性」、「和・差・比の文章題」、「速さ」の４単元からは毎年と言ってよいほど出題が見られます。

そのほかには、平面図形から点の移動に関する問題も頻繁に出題されています。頻度はそこまで高くはありませんが、図形分野からは他にも、受験生に作図を求めるような問題も出題されています。

対策方法

分野別対策法

図形対策

雙葉中学校の算数では、図形の問題がよく出題されています。なかでも図形・点の移動に関する問題がよく出題されています。点の移動の問題はしばしば旅人算や通過算の考え方を必要とする場合があります。合わせて対策しておきましょう。

まずはそれぞれの問題の典型的な解き方や公式を身につけるため、標準的なレベルの問題集をくりかえし解き、定型問題をマスターしましょう。定型問題を一通りマスターしたら過去問研究を行い、実際に出題されている問題の難易度を把握しましょう。

また当校の算数では、受験生に作図を求めるような問題が出題されています。作図の問題は問題集など掲載されている量も少ないため、過去問演習をしっかり行い、出題形式に慣れましょう。

割合と比対策

雙葉中学校の算数では、和・差・比に関する問題が4大頻出分野のうちの一つです。和と差の問題を解くときは、図や立式を工夫することで複雑な条件を整理することが重要です。普段問題を解くときから、図や式を整理して記述することを心がけましょう。

まずは標準的な内容の問題集で定型問題をマスターし、その上で過去問演習に取り組みましょう。

速さ対策

雙葉中学校の算数では、速さの問題が頻出です。なかでも旅人算や通過算の問題がよく出題されます。まずは標準的なレベルの問題集を繰り返し解き、速さの基本公式や定型問題の解法を理解しましょう。定型問題一通りマスターしたら過去問研究に移りましょう。

旅人算や通過算の問題は、立式だけでは条件を整理できず、図を描いて整理しなければいけない問題がほとんどです。また当校の算数は、問題用紙上に考え方や式を記入する方式なので、採点の際に図もチェックされる可能性があります。普段問題を解くときからきれいに、分かりやすく図を描く練習をしましょう。

計算対策

ここ最近の入試では、毎年大問1で必ず計算問題が出題されています。内容は分数・少数・整数を中心とした四則計算や逆算など、いずれも一般的な出題であるため、必ず満点を目指したい内容となっています。

とはいっても、当校の計算問題は、与えられている計算式が長く、計算処理の分量も多く複雑な問題がほとんどです。そのため計算問題だからといってあなどらず、しっかり対策をすると良いでしょう。

計算問題の対策としては、一度に大量の問題を解くというより、コツコツ少量の問題をこなしていく方が効果的です。計算問題のみを集めた問題集やドリルなども各出版社から発売されているので、自分の好きなものを1冊購入し、毎日3〜5 問程度のペースで進めていくと良いでしょう。

その際、ただがむしゃらに解くというより、入試本番と同じように慎重に解き、解き終えた後も検算をして計算ミスを減らす努力をしましょう。

問題集別対策法

【おすすめの問題集】

『予習シリーズ』 (中学受験の四谷大塚)

四谷大塚や早稲田アカデミーなどを始めとした中学受験大手塾と同じカリキュラムで算数の学習ができるシリーズ。各学年用の教材が出版されており、レベルに合った教材を選ぶことができます。予習シリーズ6年下まで一通り理解すれば中学受験における典型問題は一通りおさえることができます。予習シリーズが終了したら過去問研究に取り組みましょう。

また各ページに数問ずつ計算問題が掲載されているため、計画的に進めていけば、計算問題対策をすることもできます。このシリーズだけで基本〜標準レベルの問題をすべて網羅できる点が魅力的です。

雙葉中学校の算数で頻出の、「旅人算」の定型問題を問題集からピックアップしました。ぜひ参考にしてみてください。

【中学受験新演習　算数小6　実力アップ問題集】より

〜旅人算の問題、追いつきの旅人算と比〜

p.31〔6〕

家から学校まで行くのに姉は12分、妹は20分かかります。妹が家を出発してから６分後に、姉が家を出発して、妹を追いかけました。これについて、次の各問いに答えなさい。

⑴姉と妹の速さと比を求めなさい。

⑵姉が妹に追いつくのは、姉が家を出発してから何分後ですか。

【解説】

⑴5:3 ⑵9分後

⑴1/12:1/20=5:3

⑵姉の速さを5、妹の速さを3とすると、姉が出発する時までに妹が進んだ道のりは、3×6=18

姉が妹に追いつくのは、

18÷(5-3)=9(分後)

実際の過去問を解いてみよう！

雙葉中学校の算数では、「計算」、「速さ」、「図形」、「和と差」、「規則性」などが頻出です。これから、実際に出題された過去問を参考に、入試対策方法をご紹介します。

実際の出題例

(2019年度・第4問より抜粋)

【4】円形の畑Aと、正方形の畑Bがあります。Aの直径とBの1辺の長さは同じです。円周率は3.14です。

⑴2018年は、AとBでは同じ量の作物を収穫しました。Aでは1㎡あたり5kg収穫したとき、Bでは1㎡あたり何kg収穫しましたか。(式と計算と答え)

⑵2017年は、Aの収穫量はBの半分でした。1㎡あたりではBの方がAより1.71kg多く収穫しました。Aでは全部で何トン収穫しましたか。Aの半径は40mです。(式と計算と答え)

【解答】

⑴　3.925kg
⑵　15.072トン

【解説】

⑴
- (Aの直径)＝(Bの1辺の長さ)＝□とおく。
- Aの面積は、(□÷2)×(□÷2)×3.14=3.14÷4×(□×□)＝0.785×(□×□)
- Bの面積は、□×□
- よって、(Aの面積)：(Bの面積)＝0.785：1
- 問題文より、Aでは1㎡あたり5kg収穫されるので、
- 0.785×5÷1＝3.925
- よって、3.925kg
⑵
- ⑴より、(Aの面積)：(Bの面積)＝0.785：1である。
- (全体の収穫量)＝(1㎡あたりの収穫量)×(面積)の関係から考えると、1㎡あたりの収穫量は、A：B＝(1÷0.785)：(2÷1)
- この差が1.71kgだから、Aの1㎡あたりの収穫量は、3kgとわかる。
- また問題文より、Aの半径は40mだから、Aの面積は40×40×3.14＝5024(㎡)
- よって、Aにおける全体の収穫量は、3×5024＝15072(kg) ＝15.072(トン)

【ポイント】

雙葉中学校では、第2問以降で応用問題が出題されています。後半の問題は、前半に比べてグッと難易度が上がるものの、難問・奇問が出題さ
れるわけではありません。
全体的に解きやすい問題が多いため、高得点を目指したい内容となっています。
また、煩雑な計算を含む問題が多く、今回のように円周率(3.14)を使った問題が数多く出題されることも特徴のうちの一つと言えるでしょう。

合格点を取るには？

解答形式に慣れよう！

雙葉中学校の算数は、問題用紙上に途中式・考え方を含め解答を記入する形式です。そのため最終的な答え自体が合っていても、式や考え方についての説明が不十分であった場合、高得点を期待することはできません。

普段問題を解くときから途中式や考え方を残すようにしましょう。解答に必要な単位も自分で記述する必要があるので、抜け忘れがないように注意しましょう。

また、問題用紙上に解答を記入する欄もそこまで余裕があるわけではありません。そのため必要な式・説明を取捨選択して整理することが求められます。できるだけコンパクトな記述を心がけましょう。

4大頻出分野は過去問でマスターしよう！

雙葉中学校の4大頻出分野である、「多角形・おうぎ形の複合図形」、「規則性」、「和・差・比の文章題」、「速さ」は、ほぼ毎年出題されるほど頻出です。

昔から何回も出題されているため、過去問演習を積めば積むほど出題パターンに慣れることができます。これらの問題に苦手意識がある場合は、早急に克服しておきましょう。

計算力を磨こう！

雙葉中学校の算数では、煩雑な少数・分数計算を必要とする問題が頻出です。特に円周率(3.14)を用いる問題がよく出題されていて、そのまま解くとかなり時間を取られてしまいます。

複雑な計算処理を必要とする問題では、同類項でまとめるなど、工夫して計算量を減らしていくことが重要です。普段問題を解くときから整理して解くことを意識し、一度で答えを合わせられるよう練習しましょう。

試験が始まったらまず問題全体に目を通し、自分の得意分野や解きやすそうな問題から手をつけましょう。試験終了前の5〜10分間は見直しの時間とし、検算をしたり、解答の抜け忘れがないかどうかチェックしましょう。

まとめ

今回は、雙葉中学校の算数入試対策についてご紹介しました。

当校の算数は大問が5〜6問、総設問数10〜15問程度で、それぞれ第1問が計算問題・小問集合、第2〜5・6問が応用問題となっています。

また、当校は他の学校と比べても出題傾向に偏りがあることも特徴的です。出題パターンを把握するため、過去問研究は抜かりなく行いましょう。

算数は全科目の中で一番点差を分ける科目です。算数の点数が合否を分けると言っても過言ではないでしょう。入試本番まで時間は限られていますが、他科目とのバランスを考えつつ、限られた時間の中で優先順位に気をつけながら最大限の対策をしましょう。

参考

福久はな

こんにちは！ライターの福久はなです。
都内の中高一貫校出身で、大学受験を経て東京大学に入学しました。
塾講師や家庭教師のアルバイト経験があり、算数・数学・英語を中心に教えていました。
これらの科目に限らず、中学受験の経験を活かして理科・社会といった科目の対策方法や、学校別の受験対策、学校情報についてなど、幅広く記事を執筆しています。
皆さんの役に立つ、面白くてわかりやすい記事をお届けできるように頑張ります！