今回の記事では中学受験の算数に登場する比例と反比例について押さえていきたいと思います。受験に当たって直接比例反比例といった国が登場する事はそこまで多くないでしょうか,規則性の問題だったり受験特有の問題だったりで比例・反比例の関係が役に立つこともありますので, 知っていて損する事はありません。今回は初学者向けに記事を書いてみますが,「既に理解しているよ」という人もよければ一読してみてください。
Contents
比例とは?
それでは初めに比例と反比例について,その単語の意味を確認していきましょう。まずは比例についてです。比例とはある2つの物の関係において,片方の量が上がるとそれに伴ってもう片方の量も上がるという関係を指します。これだけだと抽象的でいささか分りづらいと思いますので,具体的な例をいくつか考えていきましょう。
よく考えられるのが,モノの値段と個数の関係ですね。ここに1個□円で売られている鉛筆があったしましょう。このとき鉛筆を2個買うと払わなければいけない値段は2×□円となり,3個買えば3×□円となります。この関係は片方の量が上がるともう片方の量も上がる,と表すことができます。
そしてこの例からもわかるように,厳密に言えば比例とは片方の値が2倍,3倍,4倍…になるともう片方の値も2倍,3倍,4倍…と増えていく関係のことを意味します。ここで出したのは値段と個数の関係でしたが,結構比例の関係は日常の至る所で見つけられます。「これは比例かな?これは比例じゃないかな?」と普段から考えてみると楽しみながら知識を定着できるかもしれません。
関係を式や表に整理すると…?
ではこの関係を式や表に整理するとどうなるか考えていきましょう。先程の例をさらに細かく問題に落とし込んでいきます。
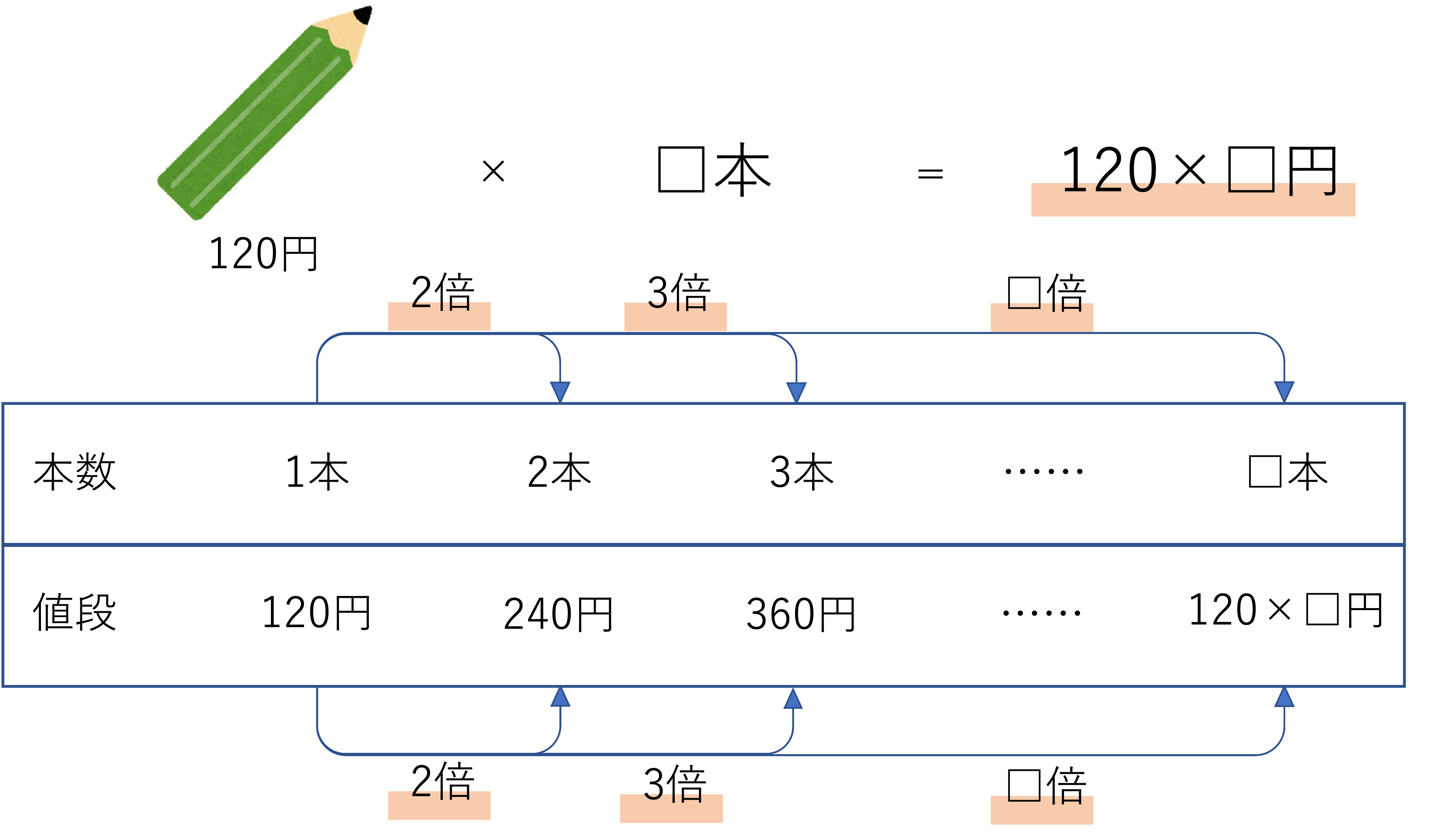
ここに1個120円で売られている鉛筆があり,それを何本か購入することにします。□本買ったときの値段を,□を使って表してください。
この問題を軸に要素を整理していきます。といっても考えることは単純で,1本買ったときの値段がいくらになるか,2本買ったときの値段がいくらになるか,…と順番に計算していけば攻略することができます。今回は2本買うと120×2で240円,3本買うと120×3で360円となりますので,これらの関係性をヒントにすると式を立てることができます。
いま鉛筆を□本買ったとしましょう。このときの値段は,当然のことに思えるかもしれませんが,鉛筆の値段を□倍したものになります。よって120×□円になる,という答えが導き出せるわけですね。これらのことをまとめると下の図のようになります。比例の単元は慣れないうちは分かりにくいかと思いますので,1本ずつ本数を増やしていくことから取り掛かると良いでしょう。
どうやって比例を判断する?
ここからはどうやって問題から「比例の関係だ」と判断すればいいのか,というコツについてお教えしていきます。そのコツはずばり,数量が変化しても大きさが変わらないかける数があるかどうかを見極めることです。今回の例題については,1本120円という鉛筆の値段は固定されていましたね。このようなかける数を基準として考えるとモノの個数と値段が2倍,3倍,…と一緒に変化するということがわかりやすく,その点で比例の関係が見えやすいです。
ただここで注意しなければいけないのが,両方が同時に増えるからと言って必ずしも比例であるわけではないということです。例えば小学生の年齢と背の高さ,などのような数字が挙げられます。小学生は基本学年が上がれば背丈も大きくなっていきますが,1年生が2年生になったからと言って身長が2倍になるわけではないですよね。その点で,倍数という観点から眺めることの重要さをご理解いただければと思います。
反比例とは?
続いてご紹介するのは反比例についてです。反比例とは2つの物の関係において,片方の量が上がるともう片方の量が反対に下がるという関係を指します。こちらもこの説明だけだと分かりづらいかと思われますので,具体的な例をいくつか考えていきましょう。
よく考えられるのが,一定数あるモノを何人かで何個ずつ分けるというものですね。例えばここに□個のアメがあったとして,これを2人で分けるのであれば1人あたりの数は□÷2個になりますし,3人で分けるのであれば1人あたりの数は□÷3個になりますね。この関係からは,分ける人数が増えると1人あたりに配られる数は減っていきます。したがって片方の量が上がるともう片方の量が下がる,と言えますね。
そしてこの例からもわかるように,厳密に言えば反比例とは片方の値が2倍,3倍,4倍…になるともう片方の値が÷2,÷3,÷4…と減っていく関係のことを意味します。ここで提示したのは人数と個数の関係でしたが,反比例の関係も色々なところで見かけられます。比例よりは見つかりづらいかもしれませんが,これはどうかな?と考えてみる癖をつけると良いかもしれません。
関係を式や表に整理すると…?
ではこの関係を式や表に整理するとどうなるか考えていきましょう。先程の例をさらに細かく問題に落とし込んでいきます。
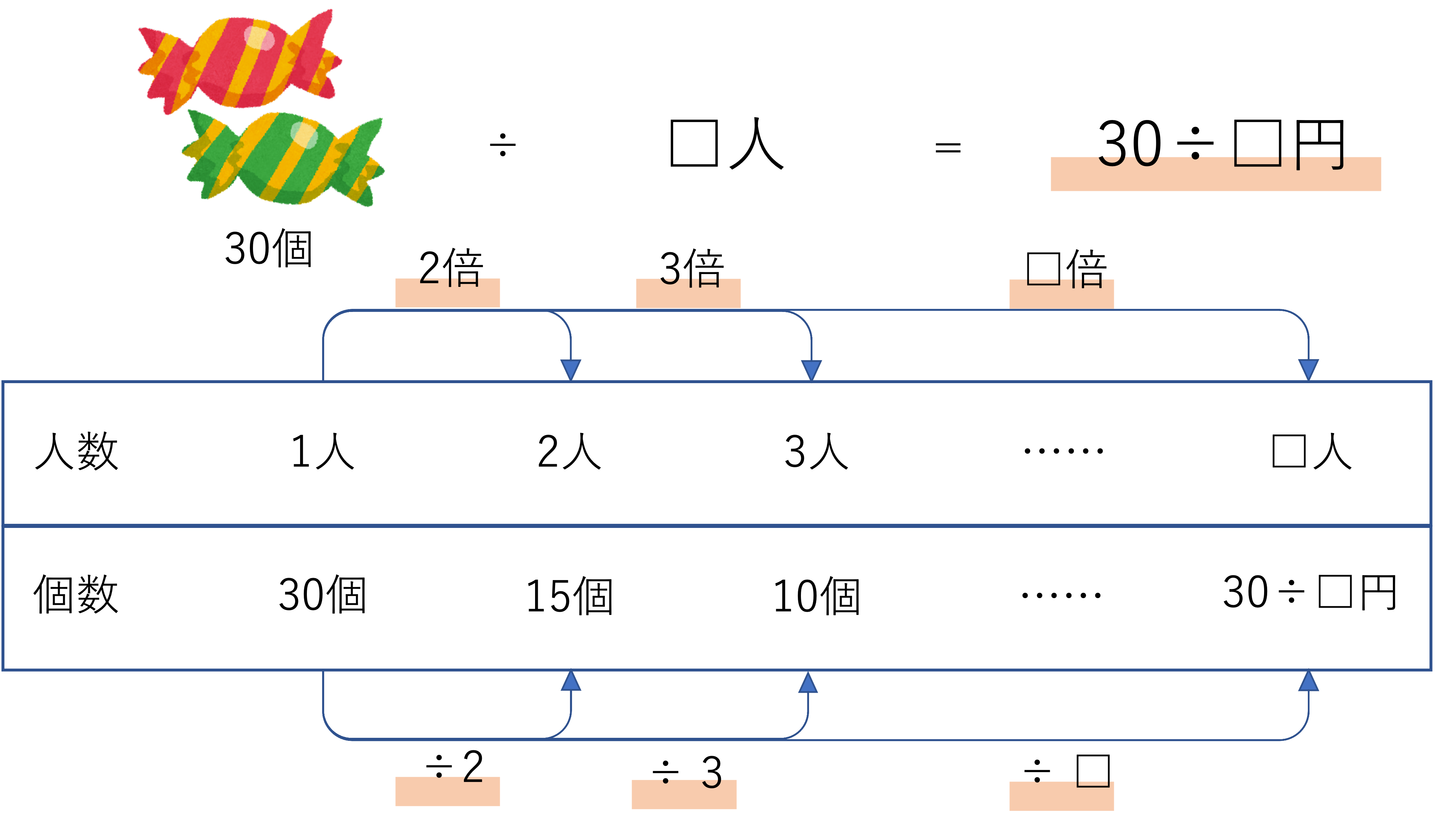
ここに30個のアメがあり,それを□人で分けることにします。このときに1人あたりに配られるアメの数を□を使って表してください。
この問題を活用しながら反比例についてまとめていきましょう。ただ比例と同様に,反比例についても考えることは至って簡単です。1人で分けるときの個数がいくつになるか,2人で分けるときの個数がいくつになるか,…と順番に計算していけば攻略することができます。割り算を行うため,人数によっては割り切れないことが発生するでしょうが,そういうときは飛ばしてしまえば問題ありません。今回は2人で分けると30÷2で15個,3人で分けると30÷3で10個となりますね。このような関係性を手がかりにすると式が立てられます。
いま□人で30個のアメを分けたとしましょう。このとき1人当たりに配られるアメの数は,30個という数を□で割ったものになります。よって30÷□個が1人あたりに配られる数になる,と導き出せるわけです。これらのことをまとめると下の図のようになります。またここで一緒に覚えて欲しいことが,人数と個数をかけ算したら一定の数になるということです。今回であれば1人×30個=30,2人×15個=30,…と元々あった30個というアメの数に等しくなりますね。割り算による関係性とかけ算による関係性を両方理解しておくといいでしょう。
どうやって反比例を判断する?
それではどうやって問題から「反比例の関係だ」と判断すればいいでしょうか。その判断基準とは,一定の数が与えられているかどうかです。今回の例題についてはアメが30個あること,そしてその値が変わらず固定していることが初めに与えられていて,この値を割っていくことで計算を進められました。この割るという計算の流れは比例にはなく反比例に特有のものです。見分けるポイントとして覚えておいてください。
ただし一点注意してもらいたいことが,増加と減少だけに注目すると判断を見誤るということです。例えば走った時間と目的地までの残りの距離,といったものが当てはまらないものとして考えられます。走れば走るほどゴールには近づいていきますが,1分から2分に時間が増えたところで残りの距離が必ずしも半分になるわけでは限りませんよね。それゆえ片方が×に・片方が÷になっているかということに注意していきましょう。
問題で比例・反比例に慣れよう!
それでは最後に比例・反比例を区別するちょっとした問題を解いて初級編の記事を締めくくりましょう。初めのうちは見分けづらいかもしれませんが,上で挙げたような判断基準を参考にして挑戦してみてください。
次の2つのものの関係のうち,比例するものと反比例するものはどれでしょう。
(1)円の直径と周の長さの関係
(2)距離が一定の道を走るときの時間と速さの関係
(3)正方形の面積と1辺の長さの関係
(4)面積が一定の長方形の縦の長さと横の長さの関係
解説
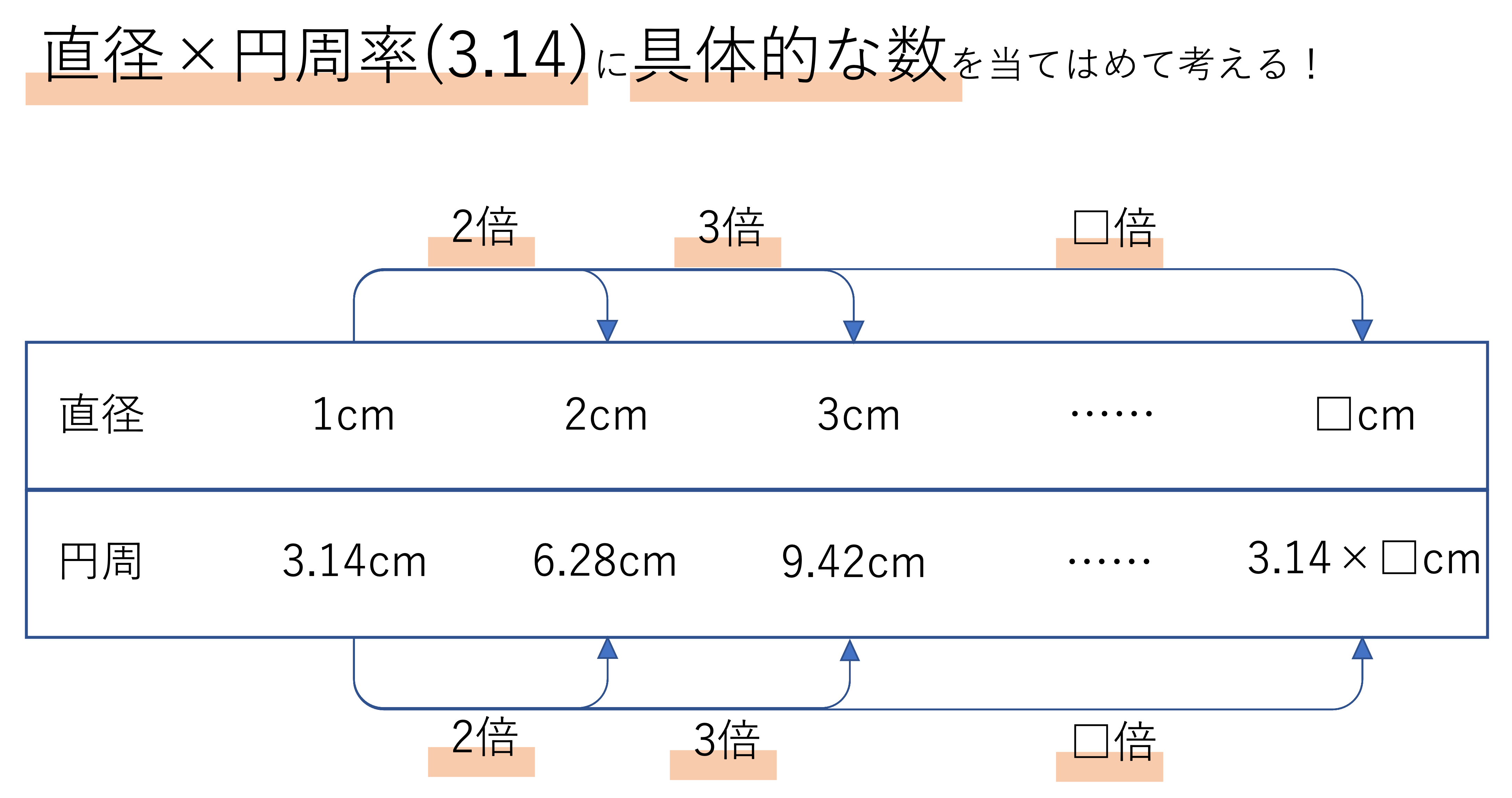
ではここからは解説に移ります。まずは(1)からです。比例と反比例を見分ける基本的なコツは,片方の数を増やして行ったときにもう片方の数がどう変化するかを考えることです。(1)であれば,直径を増やして行ったときに周の長さがどう変わっていくかを見ることで答えを導けられそうです。そこで直径を1cm,2cm,3cm…と設定していき,周の長さの変化を見ていきましょう。
いま直径が1cmだったとします。円の周の長さの求め方は直径×円周率(3.14)でしたので,この公式に基づくと円周は3.14cmになります。次に直径が2cmだとするとどうなるでしょうか。このときの円周は2×3.14で6.28になりますね。いまこの1cmの場合と2cmの場合を比べると,直径が2倍になっていて,同じように円周も2倍になっていることが判断できます。このように1cm,2cm,3cm …と数を増やしていくと,直径が2倍,3倍,…になると円周も2倍,3倍,…になることがわかります。それゆえ直径と円周の関係は比例だということになりますね。このように具体的な数を当てはめていくと問題の答えを導くことができます。
これと同じ手順で(2),(3),(4)についても考えていきましょう。(2)は距離が一定の道を走るときの時間と速さの関係です。こちらも道のりを500mだと仮に定め,時間に具体的な数を当てはめて考えましょう。例えば1分で500mを走るとすると,速さは分速500mになります。しかし2分で500mを走るとするならば,速さは分速250mで済みますね。このように1分,2分,3分…と当てはめていくと,速さがだんだん遅くなっていくことがわかります。そして1分→2分と時間が2倍になると分速500m→分速250mと半分になっているとことから,片方が2倍,3倍,…になるともう片方が÷2,÷3,…となるという反比例の定義に該当していることがわかりますね。それゆえ一定の道を走るときの時間と速さの関係は反比例ということになります。
続いて(3)の正方形の面積と1辺の長さの関係です。これも辺の長さを1cm,2cm,3cm…と任意に定めていき,それぞれの長さのときの面積を計算していきましょう。正方形の面積は1辺の長さを2回かければ計算できるので,1cmのときは1×1=1cm2となり,2cmのときは2×2=4cm2,3cmのときは3×3=9cm2となりますね。このことから辺の長さと面積は一見比例しているように見えるのですが,ここでそれぞれの関係を倍数の関係から捉え直してみましょう。
いま1cm→2cmと1辺の長さが2倍になったとして,このときの面積は1cm2→4cm2と4倍に変化しています。また1cm→3cmと1辺の長さが3倍になったとして,面積は1cm2→9cm2と9倍になっています。このことから2つの数は同時に2倍,3倍,…となっていない,つまりは比例ではないことがわかります。このようなパターンも存在することに注意していきましょう。
最後に(4)の面積が一定の長方形の縦の長さと横の長さについて考えていきましょう。これも面積を具体的に30cm2などと仮定し,縦の長さを変えていったときの横の長さの変化をみていきましょう。例えば縦が1cmだとすると横の長さは30÷1=30cmとなりますね。同様に縦が2cmだとすると横の長さは30÷1=15cm,縦が3cmだとすると横の長さは30÷3=10cmとなります。これらの関係を見ると,いま1cm→2cmに縦が2倍になったとき,横の長さは30cm→15cmと半分になっていることがわかります。このことから片方が2倍,3倍,…になるともう片方が÷2,÷3,…となるという初めに確認したことに当てはまるので,面積が一定の長方形の縦と横は反比例していることがわかります。
A.比例:(1),反比例:(2)・(4)
このようにして具体的な数を仮定したり代入したり,を繰り返していくと問題が比例に当てはまるのか反比例に当てはまるのかがわかります。慣れないうちはこのような作業を繰り返して,考え方に慣れていくといいでしょう。
まとめ
本記事では比例と反比例についての導入部分をご紹介していきました。今回は基本的な考え方についての事しかお話しできなかったのですが,グラフの書き方や少しクセのある問題など,受験に向けて対策しておきたいところはたくさんあります。中級編・上級編などレベルアップした記事でその辺りをご紹介していきたいと考えて胃ますので,そちらの記事を参照してください。本記者が今後の学習の手助けとなれば幸いです。
















