この記事では、「 平均算 」について学んでいきます。
「平均」がイマイチわからない、上手く説明できないという人はぜひ参考にしてみてください。
Contents
平均算とは
平均算はいくつかの数の平均を求めたり、逆に平均から個別の値を求めたりする問題です。平均という言葉は聞いたことはあると思いますが、その意味について考えましょう。
平均は訓読みすると「平らに均す（たいらにならす）」となります。分かりやすいイメージは、でこぼこした道を平らにする感じです（図1）。
図1
平均算ではこの考え方がとても大切です。ここから問題を解きながら解き方を学んでいきましょう。
平均算の解き方
個別の値→平均
まずは次の問題を解いてみましょう。
（例題1） A君は5回テストを受け、その点数は90点、95点、64点、73点、88点でした。A君の5回のテストの平均点は何点でしょう。
↓
解答・解説はこの下
↓
【解答】
82点
【解説】
A君の5回のテストを棒グラフで書いてみると、次の図のようになります。高さは点数を表します。
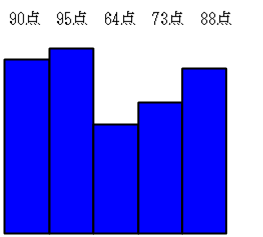図2
次に、図3のように出っ張ているところをへこんでいるところに入れてぼこぼこを平らにします。
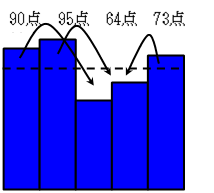
図3
するとこのようになります。
図4
この時の高さが求める平均点となります。どうしたらこの高さが求まるでしょうか。
まず、図3（凸凹を平らにしてる図）に注目してください。ここでは、出っ張ている部分をへこんでいるところに入れているだけなので、面積は変わりません。つまり、図3と図4の面積は同じです。
図3の面積は、個別の点数を全部足せばよいので、\(90+95+64+73+88=410\)です。
図4の面積は「テストの回数×平均点」で、これが410になります。
テストの回数は5回なので、平均点は\(410\div5=82\)点となります。これを公式にすると「平均＝合計÷個数」となります。
ここまでの解き方を図でまとめてみると、こんな感じです。
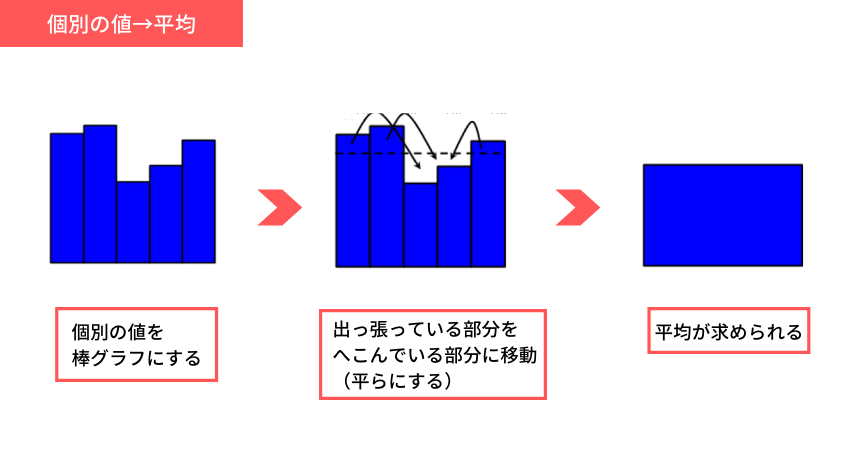
図5
次は「平均が先に与えられている」問題を解いてみましょう。
平均→個別の値
次はこちらの問題を解いていきます。
（例題2） 東京の7日間の最高気温は以下の表のようでした。またその平均は28℃でした。5日目の最高気温を答えなさい。
|
日にち |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
最高気温(℃) |
27 |
31 |
30 |
33 |
？ |
24 |
26 |
表1
↓
解答・解説はこの下
↓
【解答】
25℃
【解説】
表1を棒グラフで表すと、次の図のようになります。5日目の最高気温がわからないので、？にしておきます。
図6
上の棒グラフを平均したものが下の図です。
図7
今回は平均が分かっているので図6の面積が分かります。
図6の面積は「日数×平均」で、\(28\times7=196\)です。これが図5の面積と等しくなるのでした。
図6（棒グラフ）の面積は、7日間の最高気温を全て足すことで求まります。
5日の最高気温を？℃℃）とすると、図5の面積は、\(27+31+30+33+？+24+26=171+？\)となります。
\(171+？=196\)となるので\(？=25\)、つまり求める最高気温は25（℃）となります。
この問題の解き方をまとめてみると、こんな感じです。
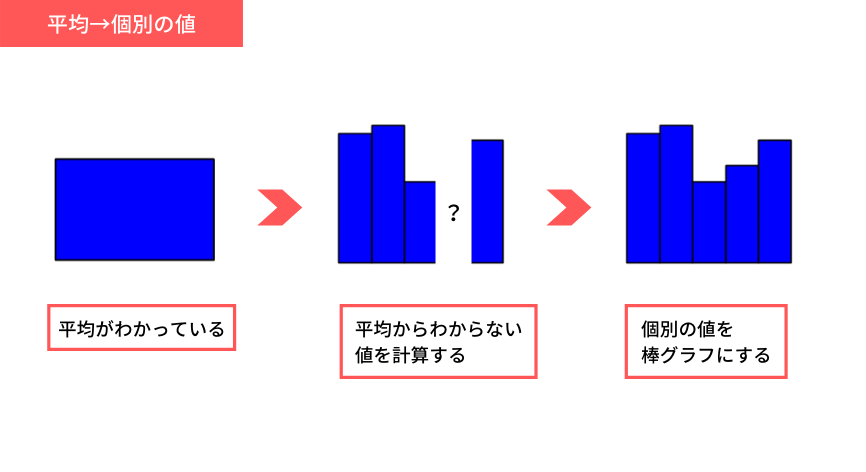
図8
先ほどの「平均を求める」問題と順番は違いますが、考え方は一緒ですね。
応用問題
平均を求める
ここでは少し難しい平均算を解いてみましょう。
（応用問題1） 男子16人、女子14人からなる30人のクラスがあります。あるテストをしたところ、クラス平均は76.4点でした。また、男子の平均点は75点でした。女子の平均点は何点でしょう。
↓
解答・解説はこの下
↓
【解答】
78点
【解説】
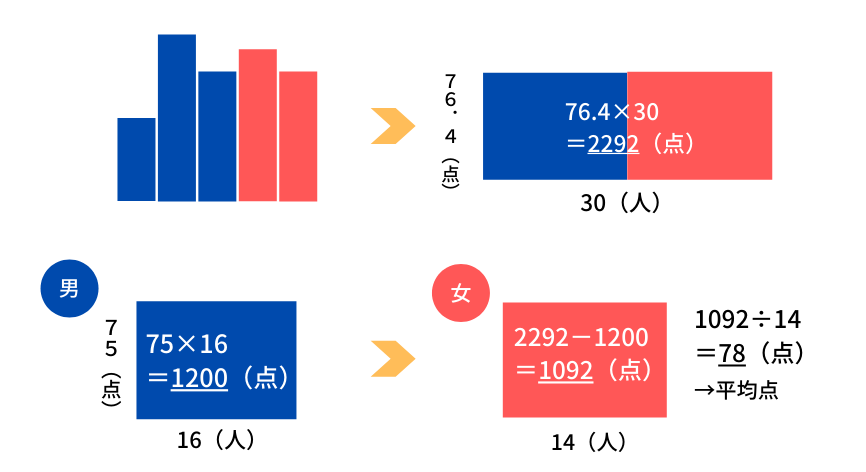
図9
「クラス全体＝男子＋女子」なので、クラス全体、男子、女子に分けて考えていきましょう。
「平均点×人数＝合計点」なので、クラス全体の合計点は\(76.4\times30=2292\)点です。
一方、男子の点数の合計は\(75\times16=1200\)点です。
「クラス全体の合計点＝男子の合計点＋女子の合計点」なので、 \(2292=1200+\)(女子の合計点) (女子の合計点)\(=2292-1200=1092\)点です。
よって、女子の平均点は\(1092\div14=78\)点です。
個数を求める
もう1問解いてみましょう。
（応用問題2） いろんな重さのりんごがいくつかあります。その重さの平均は300グラムでした。そこからりんごを5個取り除くと、残ったりんごの重さの平均は305gになりました。 りんご5個の重さはそれぞれ、313g、256g、243g、297g、296gでした。最初りんごはいくつあったでしょう。
↓
解答・解説はこの下
↓
【解答】
24個
【解説】 りんご5個を除いた後に残った個数を▢個とすると、問題文よりこの▢個のりんごの重さの平均は305gだと分かります。
一方取り除いたりんご5個の重さの平均は \((313+256+243+297+296)\div5=281\)gです。これを図にまとめると下の図のようになります。
図10
また、りんご全部の平均の重さは300gで、個数は(▢+5)個となります。これをまとめると下の図のようになります。
図11
ここで上の図の左側と、右側の面積は以下のようになります。 (左の図の面積)は\(305\times□+281\times5\)となり、 (右の図の面積)は\(300\times(□+5)\)となります。
ここで、図11の左側と右側の面積は等しくなるので下の等式が成立します。 \(305\times□+281\times5=300\times(□+5)\)
これを解くと、 \(305\times□+1405=300\times□+1500\)
左辺に□を含む式を、右辺に数字を移行し、 \(305\times□-300\times□=1500-1405\)
分配法則を使うと \(5\times□=95\)より、 \(□=19\)
つまり、最初のりんごの個数は\(19+5=24\)個となります。
まとめ……の前に
登録6000人以上！ 本サイト、中学受験ナビの監修も務めている『開成番長』こと繁田和貴が執筆する完全無料のメールマガジンでは、主に中学受験生のお子さんをお持ちの方へ向けた様々なお役立ち情報を配信中！ さらに今なら登録者にはもれなく「開成番長・繁田監修 中学受験必勝の5箇条PDF」をプレゼント！ 登録及び登録解除も簡単ですので、お気軽にご登録ください。
まとめ
いかがだったでしょうか。
簡単な問題はすぐ慣れると思いますが、難しい問題は図を書いて整理しながら解かないと解きにくいのでしっかり演習を積みましょう。
おすすめ記事
参考
東京大学理科二類の岡部信です。
京都の高校に通っていたので東京は知らないことだらけです。特に通勤電車はすし詰め状態だと聞いていましたが、ここまでだとは思ってなかったです。実家では犬を飼っていたのですが、もう3ヶ月近く会っていないのでそれが1番寂しいです。今は千葉で父と姉と3人暮らしですが、9月からは東京で1人暮らしする予定なので楽しみです。大学ではテニスサークルと東大村塾という農業と村おこしを掛け合わせたような活動をしているサークルに入っています。趣味は料理、登山です。料理は高校の時に料理研究部に入っていたのでそこそこ出来ますが、もっと上手くなれるよう時間がある時は夕ご飯を作ったりしてます。お菓子も色々作れるようになりたいです。登山は友達と休日に日帰りで行ったり、夏休みは泊まりで行ったりもしてます。今年の夏は富士山と北海道の富良野岳に行く予定です。
皆さんよろしくお願いします。
