今回はニュートン算の解き方をご説明いたします。ニュートン算とは仕事算の応用です。後ほど詳しく解説いたしますが,日常生活であまり聞き馴染みの無い言葉だとは思います。このニュートン算は中学入試において対策が必須な問題です。
しかしニュートン算そのものは一度理解してしまえばそこまで難しいわけではありません。むしろ聞き馴染みがないからこそ,少しの知識があるだけで周りと差をつけることが出来ます。今回ご紹介する問題も初歩的なものですので,よろしければご一緒に解きながら,参考にしてみてください。
ニュートン算とは何か
本節では,実際に問題に移る前にニュートン算とはどういうものか,について簡単な解説をします。ニュートン算は仕事算の応用です。仕事算では,一人一人が仕事をすればするほど全体の量も減っていく,という場合が想定されました。一方ニュートン算では全体の量が増えていきます。
このニュートン算は,その名前からも察しがつくように,かの有名なニュートンによって考案されたものです。中学受験を目指されているお子様であっても聞いたことはあるのではないでしょうか。そこでは牧場の牧草と,牧草を食べる牛の数の関係が取り上げられていました。
ここでは牧草の量が,減ったり増えたりする対象となる全体の量に相当します。牛は食べないと生きていけないので,牧草は日に日に減っていきますが,植物である牧草は成長するため,牧草は食べられるものであると同時に,増えていくものでもあります。上の「全体の数が増えていく」とはこのようなことを指します。そしてこの食べられて「減る量」と成長して「増える量」の差し引きを考えることがニュートン算の基本となるのです。
ニュートン算の基本
ここからはニュートン算の例題を解いていくことにします。よろしければ,まずはヒント無しで解けるかどうか,力試しとして挑戦してみてください。
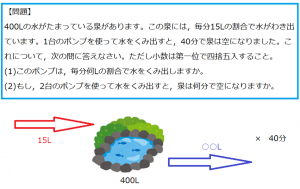
【問題】400Lの水がたまっている泉があります。この泉には,毎分15Lの割合で水がわき出ています。1台のポンプを使ってこの泉をくみ出したところ,40分で泉は空になりました。これについて,次の問に答えなさい。ただし小数は第一位で四捨五入すること。
(1)このポンプは,毎分何Lの割合で水をくみ出しますか。
(2)もし,2台のポンプを使って水をくみ出すと,泉は何分で空になりますか。
入試で問われるニュートン算のほとんどはこのような,増えたり減ったりすることが分かりやすい水槽やプール,泉といった水に関する問題になっています。
少し難易度の高い問題としてテーマパークに並ぶ人の数が出題されることもありますが,前述のとおり今回扱うのは導入であるため,人の数に関する問題は別の機会に解説できたらと思います。
例題解説
では上の例題の解き方を解説しながら,ニュートン算を解くテクニックをご紹介いたします。まず(1)に関してですが,その前に登場した数字について整理しましょう。
最初に増える量と減る量に注目します。ここでは泉の中の水の量になります。よって全体として想定しなければならないのは水の量です。そして増える量は毎分15Lであり,減る量はまだ分かりません。この区別をつけることが問題を解くカギになります。
そしてこれらの数値の区別をつけたところで,(1)の問題を解いていきます。元の量400L・15Lの増加・○○Lの減少・40分後に空になる,という情報を一つの線分図に書き起こしてみます。今回はこの図の書き方を覚えましょう。
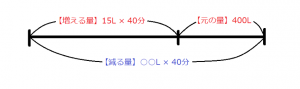
これは全体の泉の水の量を一つの線分で表し,その上に入っていた水の量と増える水の量を,下に減る水の量を書いた図です。上と下にこれらの数値が当てはまる理由は,ポンプがくみ出す水は泉にあった水だけでなく,そこに追加される水もくみだすからです。このことから次の等式が出来上がります。
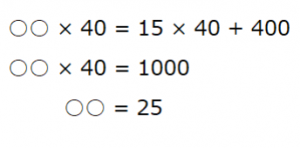
したがって(1)の答えは25Lになります。これを基に線分図を書き換え直すと,次の図のようになります。これは算数の全ての問題の共通することなのですが,分からない数値が分かったときは,必ず整理した図を更新することを忘れないようにしましょう。
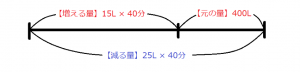
次に(2)の条件について整理します。2台のポンプで水をくみ出すとき,1台の場合は(1)で見たように25Lの水をくみ出すことが出来るので,毎分50分の水をくみ出すことになります。
この数値を整理して改めて線分図を書きます。今回はかかる時間を求める必要があるので,すべての水をくみ出すまで□□分掛かるとしましょう。
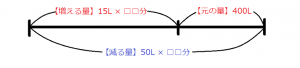
線分図はこのようになります。(2)で求められているのはこの□□の部分なので,次のように式を立て,指示通り四捨五入することで答えを導けます。
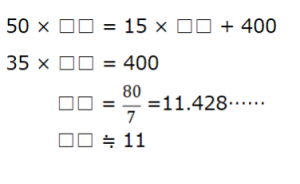
したがって(2)の答えは11分になります。このようにして線分図を書いていくとニュートン算は簡単に解く事が出来ます。元の量,増える量,減る量に注目して問題を整理することを心がけましょう。
まとめ
以上がニュートン算のまとめになります。冒頭でも述べた通り,ニュートン算は全体の量が変わるという点で他の問題よりも慣れないうちは難しく感じやすいです。そのため提示された条件を,分かりやすい形に整えることが重要となります。
本記事でご紹介したものはあくまで基礎の問題であり,慣れてくれば頭の中だけで考えることもできるようになるでしょう。ですがこのニュートン算はいくらでも条件を増やすことができ,どれほどでも難易度を上げられるのです。今回の例題でいうと,パイプから〇〇Lくみ出すときは××分だったが,△△Lくみ出すときは□□分だった,という応用問題が作れたりします。
しかしどのような問題が出てきても,線分図に表してあげると,分かっている情報と分かっていない情報が,どことどこと比較しているのか,などが明確になり,解きやすくなるでしょう。その点で線分図というテクニックは重要です。
もし似たような問題が出てきたら,増えるものと減るものを見極めること,そしてそれらを線分図に書き起こすこと,を意識して解いてみてください。
(ライター:大舘)
参考
・家庭教師のアルファ. “ニュートン算の解き方をマスターしよう” . 最終アクセス:2020/11/01















