中学入試で出題される問題のうち,平面図形は特に対策が必要となる分野です。
というのも平面図形の問題を解くためにはある種のセンスが必要になるからです。図形を分割したり,動く点や線分をイメージしたりと,直感に頼る部分が極めて多いです。そしてこのセンスは実践を通した経験で養っていくほかありません。
そのために本記事では平面図形の問題を,特に今回はおうぎ形が登場するものに焦点を当て,解説していきます。ピックアップした問題は標準的なものなので,この先出会う問題で応用できるテクニックを身につける機会にもなりうると思われます。よろしければ問題集のような感覚で,解きながら読んでいただければ幸いです。
おうぎ形が2つ登場する問題
まず初めにご紹介するのはおうぎ型2つが重なった問題です。第1問目ということで他の2問と比べるとよりシンプルなものになっています。
図のような中心角が90°,半径が6cmのおうぎ形ABCとBDEが点Bで重なり,点Dが点Bと点Cを結ぶ直線上にあります。2つのおうぎ形が重なった部分の面積を求めなさい。ただし円周率は3.14とする。(城北埼玉中学校(2017),一部改題)
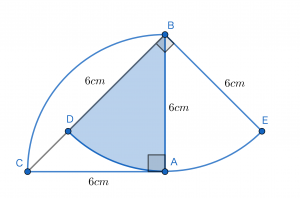
点と線が少なく,比較的わかりやすいのではないかと思われます。元の問題では点Bを中心にBDEを回転移動させる必要があり,若干複雑ではありましたが,今回は省略いたしました。よろしければご自身で一度挑戦した後に,解説で答え合わせをしてみてください。
解説
平面図形の問題を解く上で大切なのは,順序づけて計算をしていくことです。今回の問題は求める部分が単純でありますが,これは複雑な図形における問題でも同様です。
まず問題で指定されている図形について,どの部分を求めるべきかを考えます。このことは具体的にどの線分または角度の情報があれば算出できるか,を考えることに繋がります。特に図がない問題で必要となりますが,図のある問題でも同様です。
今回の求める部分の面積は上の図からも分かるようにおうぎ形です。おうぎ形の面積の公式は半径×半径×円周率×中心角÷360でした。よってこれらのそれぞれの値を算出していけばいいことが理解できます。
まず問題より円周率は3.14であることが指定されています。加えて求めるべきおうぎ形の半径は,元のおうぎ形の半径と同じ線分であるため6cmとなります。したがって中心角の大きさが分かれば面積を導けるだろう,と想定できるでしょう。
では中心角に注目し,再度図形を眺めます。中心角,つまり角DBAは,よく見ると三角形ABCを構成する角CBAと同じものであることが分かります。
よって角CBAの大きさが明らかになれば,おうぎ形の中心角がわかり,面積を導くことができる,という見通しが立てられます。ここで角CBAは,前述のように三角形ABCの一部であったため,今度は三角形ABCへと視点を変えます。
ここで辺ABと辺ACがどちらも6cmであると提示されていることから,三角形ABCは直角二等辺三角形であることが分かります。このことからその底角である角CBA・角BCAは45°だと判明し,したがっておうぎ形の中心角は45°といえます。
以上のことを基に面積を求めていくと,答えは以下のようになります。
面積=6×6×3.14×45÷360=14.13(cm2)
答え:14.13cm2
このように図形の問題は,(1)求める図形に注目する・(2)図形の構成要素に注目する・(3)計算式に当てはめる,という3ステップを踏むことが大切です。これらの手順を念頭におくと以降の2問を含めた平面図形の問題が解きやすくなるでしょう。
おうぎ形2つと半円が登場する問題
次にご紹介するのはおうぎ形と半円とが組み合わさった問題です。
下の図は,はじめに点Aを中心として半円をかき,次に点Bを中心として円の一部をかき,最後に点C を中心として円の一部をかいたものです。ABの長さが2cmであるとき,色のついている部分の面積は何cm2になるかを答えなさい。(立命館中学校(2015),一部改題)
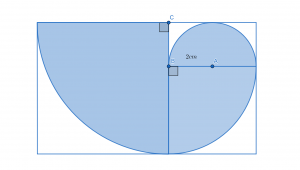
解説
この問題についても,色のついた図形を構成している部分に注目していきましょう,今回の図形は半円,小さいおうぎ形,大きいおうぎ形の3つから成っています。そのためそれぞれの面積を算出し,足し合わせることで答えを求められるだろう,と見通しが立てられます。
したがってまずは半円の面積を求めていきましょう。半円は1辺が2cmだと問題の中で提示されているため,その部分の面積は,2×2×3.14÷2=6.28(cm2)となります。
次は小さいおうぎ形の部分についても考えていきます。おうぎ形の面積を計算するためには半径と中心角の情報が必要になりますね。中心角は図より90°であることが明らかですが,半径の長さについてはここで直接示されているわけではありません。しかし小さいおうぎ形の半径は先ほどの半円の直径と同じものを指す,ということは図からも明らかです。このことからおうぎ形の半径は2+2=4(cm)であると判明し,面積は4×4×3.14÷4=12.56(cm2)である,と求められます。
同様にして大きいおうぎ形の面積についても考えていきます。大きいおうぎ形の半径は,上で確認した小さいおうぎ形の半径と半円の半径とを足し合わせた値と等しくなることが図から分かります。したがってその半径は,4+2=6(cm)となるのです。中心角は先ほどと同じように90°であるため,大きいおうぎ形の面積は,6×6×3.14×90÷360=28.26(cm2)であると計算できます。
これらのことをまとめると,図形の色のついた箇所は6.28cm2の半円・12.56 cm2のおうぎ型・28.26 cm2のおうぎ形で構成されている,と言うことができます。したがってその面積は各部分の面積の和となるため,答えは以下のようになります。
面積=6.28+12.56+28.26=47.1(cm2)
答え:47.1cm2
半円・おうぎ型・三角形が登場する問題
最後にご紹介するのは,半円とおうぎ形が出てくる問題です。やや計算が複雑になりますが,頑張って解いてみましょう。
図はAB=4cmで直角二等辺三角形と半円とおうぎ形をあわせた問題です。図の色のついた部分を求めなさい。ただし円周率は3.14とします。(城北埼玉中学校(2016),一部改題)
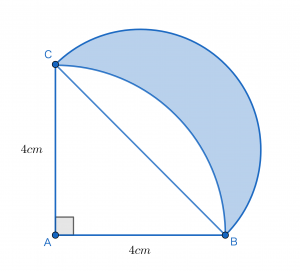
先程の問題では,求めるべき図形があくまでおうぎ形であり単純なものでしたが,今回の問題の図形は三日月型をしています。したがって図形間の足し引きが必要となり,その点で難易度が上がりますが,まずは自分の力で面積を求めてみましょう。
解説
それではここからは問題を解説していきます。まず求めるべき図形ですが,これは線分BCを直径とする半円の一部です。具体的には半円から,同じく線分BCを直径とする潰れた半円の部分を引いたもの,になります。
よって潰れた半円の面積が分かれば答えを導くことができそうです。そこで潰れた部分に注目すると,これはおうぎ形ABCから直角二等辺三角形ABCを引いた部分であることが分かります。
つまりこの問題は(1)まずおうぎ形・三角形の面積を求め,(2)その差し引きで潰れた部分を求め,(3)最後に色のついた部分を求める,と進めていけばいいわけです。ではこの手順に従って各部分を計算していきます。
まずおうぎ形ですが,この図形の半径は4cm・中心角は90°となっています。したがってその面積は4×4×3.14×90÷360=12.56 (cm2)となります。次に三角形ですが,三角形ABCはAB=AC=4cmである直角二等辺三角形であることから,その面積は4×4÷2=8(cm2)となります。以上のことからつぶれた半円の部分の面積は12.56-8=4.56(cm2)であることが分かります。
このことから色のついた部分の面積は半円から4.56を引くことで計算できますが,ここで半円の半径が提示されていないという問題が見つかります。半円の面積は半径×半径×円周率÷2でありますから,半径がわからないと先に進めません。
しかしここで改めて図形に焦点を当てなおすと,半円の直径は直角三角形ABCの斜辺に相当することが読み取れます。つまりこの斜辺BCを求めることができれば,半円の面積を求められそうです。
ここで半円の半径を□で置きましょう。このときBCは直径を指すので2×□となります。そして点Aから線分BCに向かって垂線を下ろします。垂線を下ろしたとき,新たに2つの小さな直角二等辺三角形が生まれますね。すると半円の半径はこの垂線の長さと等しくなることが分かります。
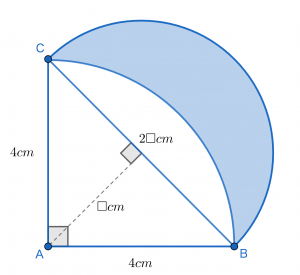
このことから三角形ABCの面積を新たに書き起こしていきましょう。BCを底辺,垂線を高さとみなすと,面積=2×□×□÷2と表すことができ,このときの面積の値が8であることから,2□×□÷2=8という式が成立します。
これを単純にすると,×2と÷2の部分が相殺されるため,□×□=8となります。これを言葉で説明すると,半円の半径は「2回かけたら8になる数」であるということを指します。
以上のことから,半円の半径をそのまま求めることはできませんでしたが,その値は2回かけたら8になる数であることが発覚します。このことを元に半円の面積を求める式を立てると,面積=□×□×3.14÷2という関係が導かれ,この式を解いていくと,□×□×3.14÷2=8×3.14÷2=12.56(cm2)となります。
以上のことから,色のついた部分は12.56cm2の半円から4.56cm2の潰れた部分を引くことにより求められます。このことから答えは次のようになります。
面積=12.56-4.56=8(cm2)
答え:8cm2
まとめ
今回はおうぎ型に関する平面図形の問題を3つ紹介いたしました。第1問目でご紹介した通り,この範囲では図形に注目する・構成要素に注目する・計算式に注目する,と視点を移していくことが大切です。よろしければこのテクニックを意識して様々な問題に挑戦してもらえればと思います。
(ライター:大舘)
















