今回は平面図形の おうぎ形 と円の入試問題の中から,とりわけ難易度の高い応用問題を3問ご紹介いたします。
このような応用問題は基礎を身につけた上で挑戦するのが望ましいです。難易度の高い問題ほど解ければ周りの受験生と差をつけられます。基礎固めがある程度完成したらきちんと対策しておきましょう。
本記事では一見簡単そうに見えて実は難しいといったものから,難しそうに見えるが頻出されるパターンに則っているため実は簡単なものまで取り揃えました。宜しければ,テキストのような感覚で実際に問題を解きながら進めてもらえればと思います。
Contents
【 おうぎ形 ①】三角形とおうぎ形に関する問題
初めにご紹介するのはおうぎ形の中に三角形が含まれている,という図形に関する問題です。1問目ということでやや標準的な難易度のものをピックアップいたしました。まずは解説を読む前に,実力で解けるかどうかチャレンジしてみましょう。
図は半径4cm,中心角が45°のおうぎ形と二等辺三角形を組み合わせた図形です。AD=BDのとき,色のついた部分の面積を求めなさい。ただし,円周率は3.14とします。(慶應義塾中等部(2015),一部改題)
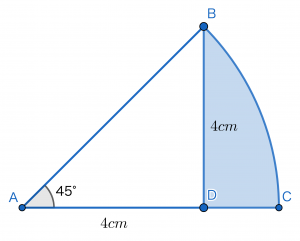
解説
それではここからは上の問題の解説に移ります。本問題は平面図形でも比較的簡単な,構成されている図形同士の足し引きによって解くことができる問題です。
図形の中におうぎ形があり,その中に三角形があることは図からも明らかです。そして「おうぎ形の面積」-「三角形の面積」により問題を解くことができそうだ,見通しが立てられます。したがっておうぎ形・三角形の面積をまずは求めなければいけません。
したがってまず三角形について考えていきます。この三角形ABDは,AB=AD=4cmの直角二等辺三角形です。そのため面積は公式通り,ADを底辺,BDを高さとすると,4×4÷2=8(cm2)となります。
次におうぎ形について考えます。おうぎ形の面積を求めるためには,半径と中心角の値が必要です。中心角は45°であるので,半径がいくつなのかを計算しましょう。ここでおうぎ形の半径は三角形の斜辺ABに等しいです。そのためこの斜辺を,三角形の底辺と高さの関係から求めていきます。
上で求めたように,三角形ABDの面積は8cm2でした。このときはADを底辺・BDを高さとして計算しましたが,この面積は別の底辺・別の高さを使って計算しても変わりません。このことから,斜辺ABを底辺として改めて三角形ABDの面積について考えていきましょう。
ABを底辺としたとき,三角形の高さはDからABに降ろした垂線となります。このとき三角形ABDの中には小さな直角二等辺三角形2つが生まれることが分かるでしょうか。その1辺を□cmとすると,高さは□cmになります。そしてABは小さな直角三角形の1辺が2つ並んだ線分であるので,2×□=2□cmと表すことができます。
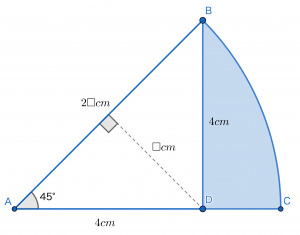
したがって三角形の面積に関して,2□×□÷2=8という式が成り立ちます。これを簡単にすると,×2の部分と÷2の部分が相殺されるので。□×□=8という式が出来上がりました。つまりは□,2回かけると8になる数であることが判明します。
このことを元に再度おうぎ形について考えましょう。おうぎ形の面積は半径×半径×円周率×中心角÷360でした。いま半径は2□cm・中心角は45°・円周率は3.14だと分かったので,式を組み立てると,面積=2□×2□×3.14×45÷360となります。
あとはこの式を解いていくだけです。□×□の値は前述より8であるため,面積=(2×□)×(2×□)×3.14×45÷360=4×□×□×3.14×45÷360=4×8×3.14×45÷360=3.14=12.56(cm2)と値を求められました。
以上をまとめると三角形の面積は8(cm2),おうぎ形の面積は12.56(cm2)となることから色のついている部分の面積は12.56-8=4.56(cm2)です。
答え:4.56(cm2)
1問目のまとめ【 おうぎ形 ①】
この問題では提示されている図の中の図形に注目できるかどうか,そして底辺と高さの関係に注目して線分を算出できるか,が問われていました。
このようなテクニックは平面図形の範囲を取り組む上で重要になります。これを機会に覚えてしまいましょう。
- 平面図形では図形の中にある図形に注目する!
- 分からない線分があるとき,それが三角形の一部だったら面積・底辺・高さの関係に注目する!
また惜しくも計算ミスで間違えてしまったり,□と2×□を混同してしまったりした人は,次の問題では気をつけて計算していきましょう。
【おうぎ形 ②】半円・円・おうぎ形に関する問題
次にご紹介するのは,おうぎ形と半円と円とが絡んだ問題です。これも同じようにまずは自分の力で解いてみましょう。
図は,大きな半円と小さな円と直線を組み合わせたものです。図の色のついている部分の面積を求めなさい。ただし,円周率は3.14とします。(浦和明の星女子中学校(2019),一部改題)
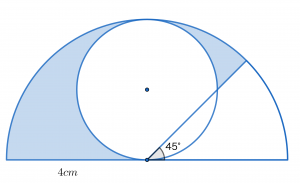
解説
ここからは解説をしていきます。今回の問題は3種類の図形が登場しました。そして1問目と大きく違うところは,色のついた部分が大きい左側と小さい右側に分かれていることです。その点で若干解きづらいかもしれませんが,この問題も図形の足し引きで計算することができるのです。
しかし今回の問題では補助線を引く必要があります。それは図からも分かるでしょう。おうぎ形から円の一部が欠けたものを引くことで計算できますが,この欠けた部分を計算するのは難しそうです。
ではどこに補助線を引くことが正解なのでしょうか,おそらく何通りかの方法が挙げられるでしょうが,ここでは次のように補助線を引いてみましょう。
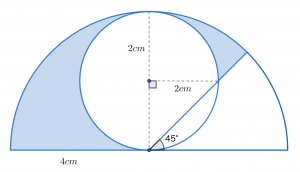
提示された円の中に,半円の中心を通るような直径と,直線と半円の交点を通る半径を引きました。この操作により色のついた部分は2つに分けられます。
そしてそれぞれについて構造を確認すると,左側は中心角90°のおうぎ形から半円を引いた形・右側は中心角45°のおうぎ形から直角二等辺三角形と中心角90°のおうぎ型を引いた形になっていることが分かるでしょうか。
したがってこの問題の答えは,以上のおうぎ形・半円・三角形を求めていくことで導き出せそうだ,と見通しが立てられます。このように直径や半径を利用して補助線を引くことが今回のテクニックになります。
では補助線による図形の分解が達成できたところで,面積の具体的な数値を求めていきましょう。まず左側の部分から考えていきます。改めての確認ですが,左側の図形は中心角90°・半径4cmのおうぎ形から半径2cmの半円を引いたものでした。したがってその面積は,4×4×90÷360×3.14-2×2×180÷360×3.14=12.56-6.28=6.28 (cm2)となります。
次に右側の部分について考えていきましょう。右側は半径45°・半径4cmのおうぎ形から,半径2cm・中心角90°のおうぎ形及び1辺が2cmの直角二等辺三角形を引いたものですので,4×4×45÷360×3.14-(2×2×90÷360×3.14+2×2÷2)=6.28-(3.14+2)=1.14(cm2)だと求められます。
このことから右側と左側の面積を足すと,6.28+1.14=7.42(cm2)となるため,答えは次のようになります。
答え:7.42cm2
2問目のまとめ【 おうぎ形 ②】
この問題では適切な場所にいかに補助線を引けるか,が問われているものでした。そして引いた補助線を元に図形同士の足し引きを考える,という2段階のステップを踏まなければいけなかったことに,難しいと感じるポイントがあったかもしれません。
したがって平面図系の問題を解くにあたっては次のようなテクニックも求められます。覚えておきましょう。
- 補助線を引くときは,中点や交点・頂点をつなぐように考えていく!
特に線分や直線の交点に関しては図の中でも比較的目立ちにくいです。平面図系の問題を見たら,早いうちに図のなかに交点がないかを確認し,補助線の手がかりになるかもしれないので印をつけておきましょう。
【 おうぎ形 ③】半円と おうぎ形 に関する問題
最後にご紹介するのはおうぎ形と半円2つが重なった図形の問題です。
図3は,半径が10cm,中心角が90°のおうぎ形に,直径が10cmの半円を2つかいたものです。色のついた部分の面積を求めなさい。ただし,円周率は3.14とします。(渋谷教育学園幕張中学校(2012),一部改題)
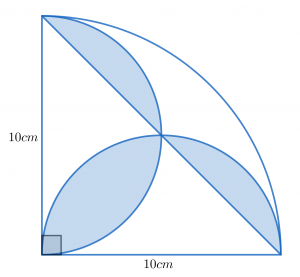
この問題も2問目と同様に簡単には解けそうにない図形の面積が求められています。したがってまた補助線を書き入れる必要がありますね。どの部分に書き込むかを考えながら,試しに解いてみましょう。
解説
それではまず,単なる図形の足し引きだけでは解けそうにないことは問題からも明らかなので,2問目と同様に補助線を引いてみましょう。
このとき上で確認したテクニックを使ってみます。今回は半円の弧が重なっているため,その交点に注目します。ではその交点とどの点を結べばいいか,お気づきでしょうか?
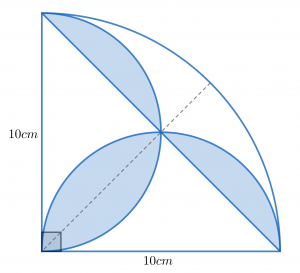
円の中点から半円の交点に向かって線分を引いてみました。このような補助線を引くことで,複雑な図形は潰れた半円4つに分割されます。つまりこの潰れた半円の部分の面積が分かれば,求める面積を算出できるわけです。
ではこの1個あたりの面積はどのようにして求めればいいのでしょう。このとき,下にある半円に注目してみましょう。
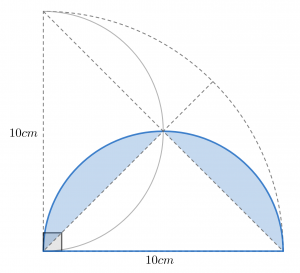
下の半円に注目すると,元から提示されている直線と新たに引いた補助線により,半円は直角二等辺三角形と潰れた半円2つに分割することができます。つまり半円から三角形の面積を引くことで,2つ当たりの面積が求まるわけです。そしてその2倍として色のついた部分を考えることができます。
では実際に半円と三角形の面積を計算していきます。まず半円ですが,これは半径5cmなので,面積は5×5×3.14×180÷360=39.25(cm2)となります。
次に三角形の面積を求めていきます。この三角形の底辺と高さは直接図に書かれているわけではありませんが,三角形は図の中に存在する底辺10cm・高さ10cmの大きな三角形の半分になっています。そのため三角形の面積は10×10÷2÷2=25(cm2)となります。
このことから,潰れた半円2つの面積は39.25-25=14.25(cm2)だと計算でき,求める図形はこの潰れた半円4つがくっついたものであったので,最終的な答えは14.25×2=28.5(cm2)となります。
3問目のまとめ【 おうぎ形 ③】
この問題でも2問目と同様に適切な場所に補助線が引けるか,そして1問目のように図の中で図形の足し引きを考えられるか,という能力が必要となっていました。
また今回の問題に関しては,あえて潰れた半円1つ分ではなく2つ分の面積を考えていくことで,計算を簡略化することが可能になっています。
同じ図形でもいろいろな切り取り方ができますが,その中で一番簡単に計算できそうなものを選ぶ技術も中学受験の平面図形では大切です。
追加練習用プリント(無料)
練習用プリント(無料)は、
『個別指導塾テスティー』の公式LINE の友だち追加された方のみの配布となっております。
以下から公式LINEの友だち追加をして、記事の続きをお楽しみください!!
≪入手方法≫
※画像はあくまでイメージです。本来送られるものとは違いますのでご了承いただけますよう、よろしくお願い致します。
①以下のリンクから公式LINEを友だち追加
②送信される画像をタップ!
パスワードで保護されている記事へと移動します。

③パスワードを入力(パスワードはLINEの友だち追加時に送信いたします。)
※パスワードを入力しても見ることができない場合、もう一度入力していただくか、キャッシュ機能の設定を変更するなどしていただきますよう、お願いいたします。

④スクロールしてPDFをダウンロード!

<スマートフォンからお読みの方はこちら>

<パソコンからお読みの方はこちら>

まとめ
今回はおうぎ形に関連した平面図形の応用問題を3つご紹介いたしました。もちろんこの他にも出題のパターンは存在しますが,改めてここで確認したテクニックを振り返っておきましょう。
- 平面図形では図形の中にある図形に注目して解く!
- 分からない線分があるとき,それが三角形の一部だったら面積・底辺・高さの関係に注目する!
- 補助線を引くときは,中点や交点・頂点をつなぐように考えていく!
- 図形は計算が一番簡単になるように切り取る!
以上になります。前述の通り平面図系の応用問題は基礎がしっかり身に付いていないと解くのは厳しいですが,その分対策をしっかりすると周りと大きな差をつけられます!よろしければ今後演習を行う際には,これらの点に注意してみてください。
(ライター:大舘)















