今回は平面図形の面積に関する問題の解き方をご説明します。平面図形とは文字通り平面上にある,点と線で構成された図形です。身近なものだと三角形や正方形が該当しますが,中学受験の算数でそのような単純な図形が出題されることはめったにありません。
補助線を引いたり,図形から図形を引いたりと色々なテクニックを使って解く必要がありますが,図形のどの部分に目を付けたらいいのかよく分からない人も多いと思います。実際筆者も平面図形の問題は苦手でした。
しかし少し視点を変えて図形を眺めてみるとこの手の問題は解けるようになります。本ページではそのためのコツをご紹介します。もちろんこのコツはすべての問題が解けるようになるという魔法ではありませんが,今後の勉強の手掛かりになれば幸いです。
難関校で出される複雑な図形のタイプ
まず中学受験で出される複雑な図形について知っておきましょう。試しに平面図形の問題を中学入試の過去問から引っ張ってきました。自分ならどう解くか,を考えながら目を通してみてください。
半径5cmの半円を,4つの直線によって次のように分けます。ここでC,D,Eは直径ABを4等分する点です。また下のような角度が与えられています。円周率が3.14であるとき,アの面積は何cm2ですか。(麻布中学校(2018),一部改題)
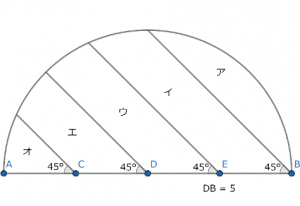
図1
いかかでしょうか?すぐに答えまでたどり着けそうだなと感じた人もいるでしょうし,とりあえず頭の中で補助線を引いてみた人も,まったく分からないという人もいるでしょう。
麻布中学校ではこの問いの他に「イ+エの面積からウ+オの面積を引いた値を求めましょう」という問いも出されていました。そのためもし麻布中学校の入試を受けるのだとしたら,素早くアの面積を求め,その次の問題に移る必要があります。
ですがたとえ今難しく感じても,どこに注目すればいいか,が分かるようになるとさらさら解けるようになるでしょう。今回はこのアの面積を求めながら,複雑な図形問題の切り口をご紹介いたします。
平面図形の問題は一癖も二癖もあるものが多いですが,その分実力が付けば周りと差をつける得点源に変わります!いま考える中でつまずいてしまった人は実力を伸ばすために,簡単に解けた人は更なる応用問題への挑戦のために,本記事を参考にしてみてください。
複雑な図形の面積を求める「コツ」
それでは改めて上の図形を参照しながら,面積を求めるコツをご紹介いたします。もう一度アを眺めてみると、薄いかまぼこ型をしていることが分かります。
ここで確認したいのが,「このようなかまぼこ型の図形の面積を小学校で習ったか」ということです。三角形であれば底辺×高さ÷2,長方形や正方形であれば底辺×高さ,のようにかまぼこ型の面積を求める公式をご存じでしょうか?
もちろんそのような公式は聞いたことがないはずです。中学入試の問題は小学校で習った知識の組み合わせで解けるようになっています。これは裏を返せば、小学校で習っていない知識から出題されることはない、ということを指します。
一部の学校の理科や社会の科目では並の小学生が知らないことを問われることもあるでしょうし、実際高等な知識を身に着けていることで有利に働く可能性もあるでしょう。しかし多くの中学校は知恵の部分を重要視しているはずです。
したがってアの面積は,これまで習った三角形・長方形・ひし形・台形・平行四辺形・円・扇形の面積を組み合わせて計算できるように作られていることが分かります。そしてこのような出題範囲の限界が複雑な図形問題を解くコツに繋がるのです。
つまり「複雑な図形問題はこれまで習った簡単な図形の組み合わせとして考えればいい」ということが今回のコツとなります。そしてパズルのようなイメージに基づいて、補助線を引いたり、面積を求めたりすればいいのです。
ではこのコツを基に上の図形をもう一度眺めてみましょう。まずアを形作る線のうち、左上から右下のBに向かってまっすぐ伸びる線がありますね。そしてBから円の中心Dに向かって半径が伸びています。このDと最初に見た線の左上の端を結ぶと三角形が浮かびあがることが分かるでしょうか?
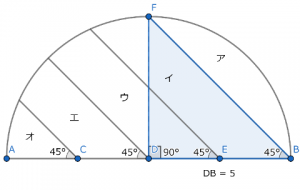
図2
こう見ると、アは扇形の部分からDを直角とする三角形を取り除いた余りのように考えられますね。先ほど「パズルのように」とご説明いたしましたが、要するに○○を求めなさい、という指示が出ているところが,平面図形をはじめとする算数の応用問題が分かりづらい原因の一つにあるかと思われます。この問題の場合面積を求めてください、という言葉がその指示に当たります。
ですが頭の体操のように「この図形に一本線を引いて三角形を作りなさい」と言い換えると,問題は一気に分かりやすくなるでしょう。
つまり今回お伝えしたかったコツとは「面積を求める前に、図形の中にいろんな小さな図形を作ってみて,その組みあわせとして面積を計算しましょう!」ということなのです。
実際に「コツ」を使ってみる
それでは上で確認したアの捉え方からその面積を求め,この記事の締めくくりといたしましょう。アは扇形から三角形を引いた余りの部分と考えられましたね。そのため初めに扇形の面積と三角形の面積を別々に求めていきます。
まずは扇形です。復習ですが,扇形の面積は次のように求めることが出来ました。
半径×半径×円周率×中心角÷360°
このとき問題において半径の値は5cmであり,円周率は3.14であることから中心角,つまりは∠FDBの大きさが分かれば面積を求められそうです。
ここで半径は等しいことから△DBFはDFとDBが等しい二等辺三角形であり,∠DFB=∠DBE=45°であることから,中心角は直角であると証明できます。このことから扇形の面積は次の通りです。
扇形の面積=5×5×3.14×90°÷360°=19.625(cm2)
続いて三角形の面積を求めていきます。上で見たように,∠FDBは直角です。このことから三角形の底辺は5cmであり,高さも5cmであることが分かります。よって三角形の面積は次のようになります。
三角形の面積=5×5÷2=12.5(cm2)
ここまで来たらあとは引き算をすればアの面積が分かります。
アの面積=19.625-12.5=7.125(cm2)
以上のことから答えは7.125cm2となります。計算の部分で小数が出てくる点がやや厄介な問題ですが,考え方が分かれば簡単に思えたのではないでしょうか。
最後に繰り返しになりますが中学入試に挑むにあたって平面図形の問題の対策は欠かせません。よろしければこの手の複雑な図形問題は直接面積について考える前に,「図形の中に図形を作る」という段階を踏むことを意識して,演習を重ねてみてください!
(ライター:大舘)

















