今回の記事では水量変化とグラフに関する問題を取り扱うシリーズの第2段目として、実際の受験問題を3問引用しながら、応用的な攻略方法をご紹介していくものになります。この問題は立体や速さや比率といった様々な範囲の要素が寄せ集められているため難しく感じやすいですか、その分少しの理解があれば、設問が1つでも解ければ周りと大きな差をつけることができますので、しっかりと対策していきましょう。
Contents
「水量変化とグラフ」とは…?
まずは基礎編の振り返りとして、「水量変化とグラフ」とはどういう問題だったかをおさらいしていきましょう。この分野は空間図形と速さが大きく関わってくる問題です。中には割合と比に関する問題が登場することもありますが、ともかくさまざまな領域の要素が関連して1つの問題を作り上げていることに大きな特徴があります。
水量変化とグラフからの出題において特徴的な点としては、立体の存在・グラフの存在・水を入れたり抜いたりする状況という3つが挙げられましたね。そしてこれらの要素が関わっている問題を攻略するポイントとしては、まず立体を平面に置き換えることで水の貯まる様子をイメージしやすくし、その後立体の形や問題の状況に沿って発生するペースの転換を押さえ、1分あたりの変化や貯まるまでの時間といった情報をまとめて答えを適切な形で導くことをご紹介いたしました。今回引用する問題はすべてこのような攻略法に則れば無事答えが求められますので、慣れないうちは時間こそかかるかと思われますが、じっくり挑戦してみましょう。
問題① まずはスタンダードな問題!
それではここからは問題演習に移っていきます。はじめに引用するのはスタンダードな問題です。設定こそやや複雑ですが、上でご紹介したテクニックを使えば無事解くことができますので、完全正答目指して頑張ってみましょう。
下の図のように直方体の容器Aの中に、直方体の容器Bが入っています。蛇口から毎秒40cm3ずつ一定の割合で容器Bに水を入れるとき、次の問いに答えなさい。
(1)容器Aに水が入り込むのは、水を入れ始めてから何秒後ですか。
(2)容器Aが満杯になるのは、水を入れてから何秒後ですか。
(3)水を入れ始めてから22秒後に容器Aに入っている水の深さを求めなさい。
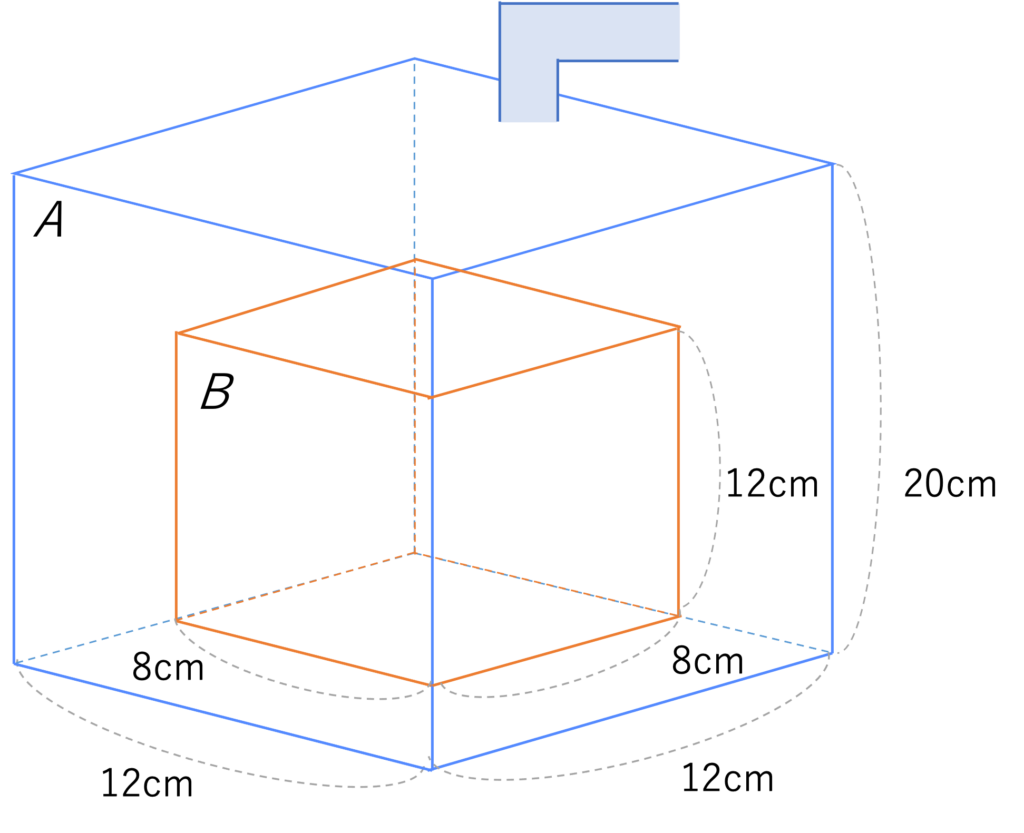
(明治学院中学校(2012)、一部改題)
解説①
ここからは解説に移ります。今回の問題は水そうの中に一回り小さい水そうが存在する、という形の立体が登場していました。基礎編で扱ったような立体が組み合わさった形ではないので戸惑ってしまうかもしれませんが、基本的な解き方は同じです。むしろグラフが登場しない分ときやすいかもしれませんね。そのため、まずは問題文や図形の情報を整理していきましょう。はじめに実施するのは立体を平面に置き換えることです。今回の図形でBの直方体とAの直方体がくっついていることに注目すると下のような図を書くことができます。このときAの奥行きが12cm・Bの奥行きが8cmであることを忘れないように覚えておきましょう。
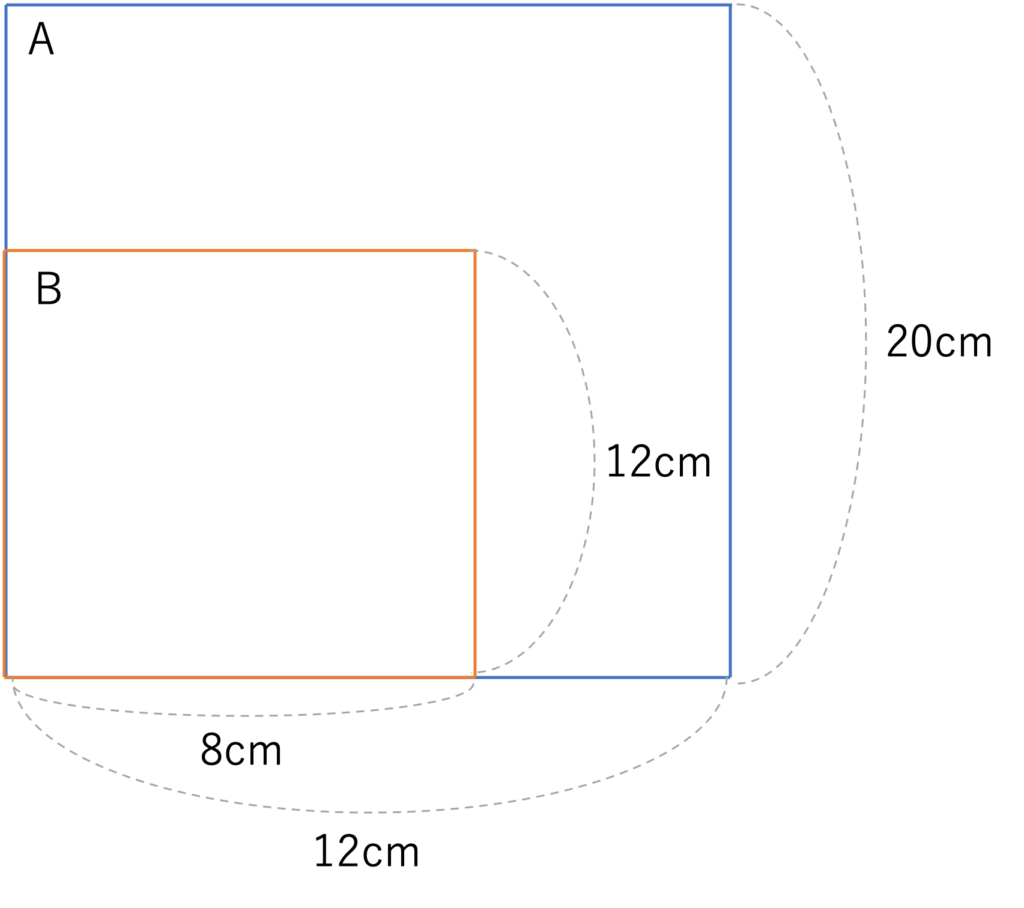
さてこの図をもとに(1)から解答を進めていきます。まず問われているのは容器Aに水が入り込む時間です。ここで上の図およびBに水を入れていくという設定に注目すると、Aに水が入り込むのはBが水で満たされてからになりますよね。いま容器Bの容積が8cm×8cm×12cm=768cm3であり、容器Bには1秒間に40cm3ずつ水が入れられることから、Bを満たすのにかかる時間は768÷40=19.2となるため答えは19.2秒後となります。このように平面の図を書くことで水の動きがイメージされやすいです。また今回は答えが19.2という小数になりましたが、中学受験では秒数をはじめとした時間が小数・分数の形で答えとなることがよくあるので、慣れないかもしれませんがしっかり覚えておきましょう。
A(1)19.2秒後(5分の96でも可)
続いて(2)の問題に移ります。これまでの情報をまとめると次のような図に整理できます。
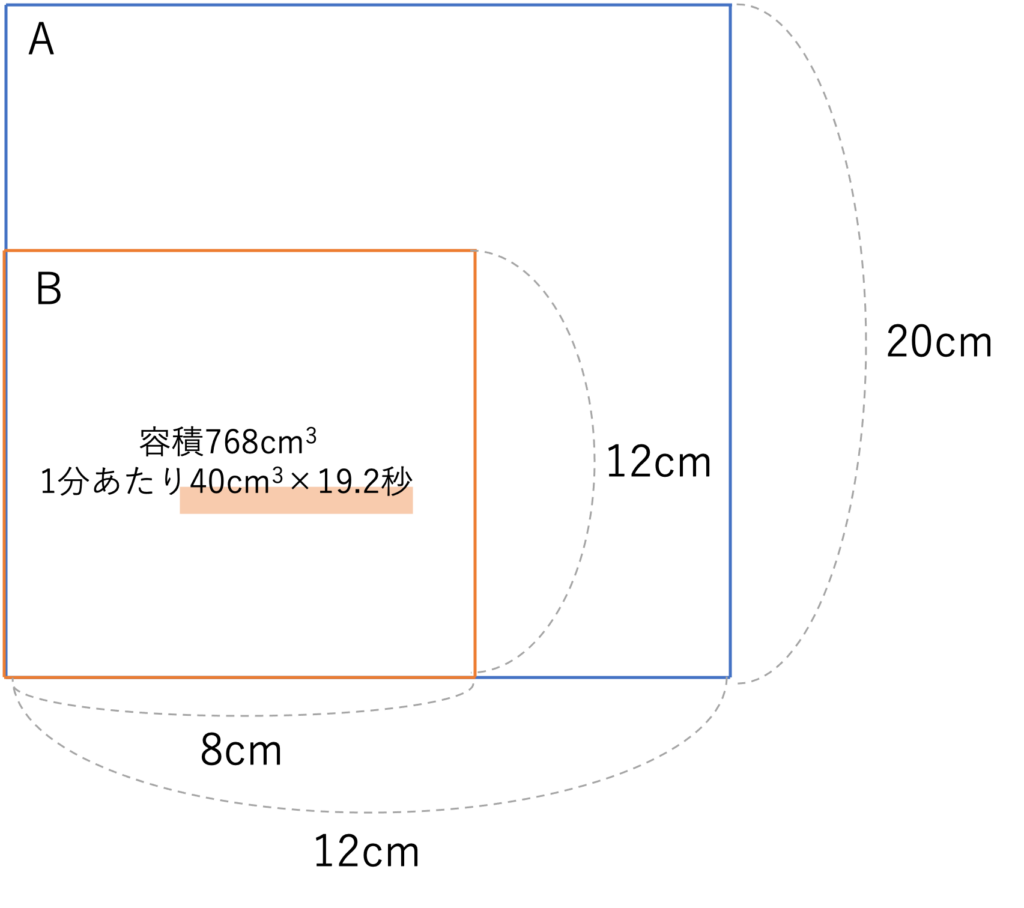
この図から(1)と同じ手段で解くのであれば、Aが満杯になる時間を計算するには、容器Aの中で容器Bが占めている部分以外の容積を考えていけばいいのではないか、という想定ができるかと思われます。しかし今回の問題はより簡単に解けます。というのもBはAの一部ですので、問題で行われていることは容器Aに40cm3ずつ水を入れていることと変わらないのです。それゆえかかる時間はAの容積を40cm3で割ることで求められるわけです。いまAの容積は12cm×12cm×20cm=2880cm3であるので、答えとなる満杯までの時間は2880cm3÷40cm3=72秒となります。
A.(2)72秒
では最後に(3)を解いて問題を締めくくっていきましょう。まずは(3)の中身に入る前に(2)までで求めた内容をまとめておきましょう。このように少しずつ情報をまとめておくことで後から振り返りやすくなるので、余裕を持つためにも実践してみてください。
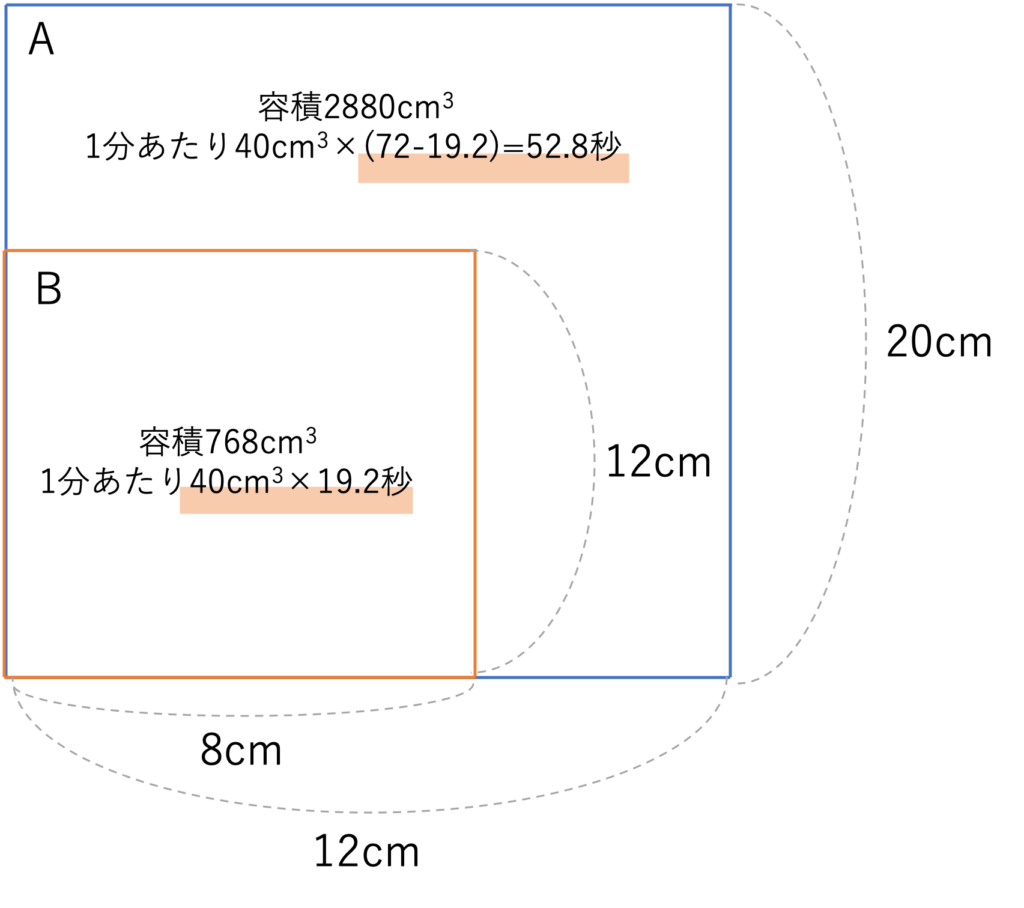
さて最後に求めるのは22秒後の容器Aに入っている水の深さですね。上の図から水を流し始めてから22秒後というのは、容器Bが水で満杯になる19.2秒後より2.8秒多く経過しているので、その分である2.8秒×40cm3=112cm3が容器Aの中に入っているわけです。ここでこのときの容器Aに注目すると、Bが一部分を占めているため、その部分が凹んでいるような形になっています。したがってまずはAをBの高さまでである12cmの部分とそれより上の部分に分け、それぞれにどれくらい水が入るのかを考え、112cm3という水の量がAのどの辺りまで達するかをざっくり考えていきましょう。まず12cmまでの部分の容積を考えると、この部分の底面積はAの底面からBの底面を引いた(12cm×12cm)-(8cm×8cm)=144cm2-64cm2=80cm2となり、高さが12cmなので80cm2×12cm=960cm3となります。他方12cmより上の部分に関しては,底面積はAの元々の底面である12cm×12cm=144cm2と変わらず、高さは20cm-12cm=8cmとなるので144cm2×8=1152cm2となります。
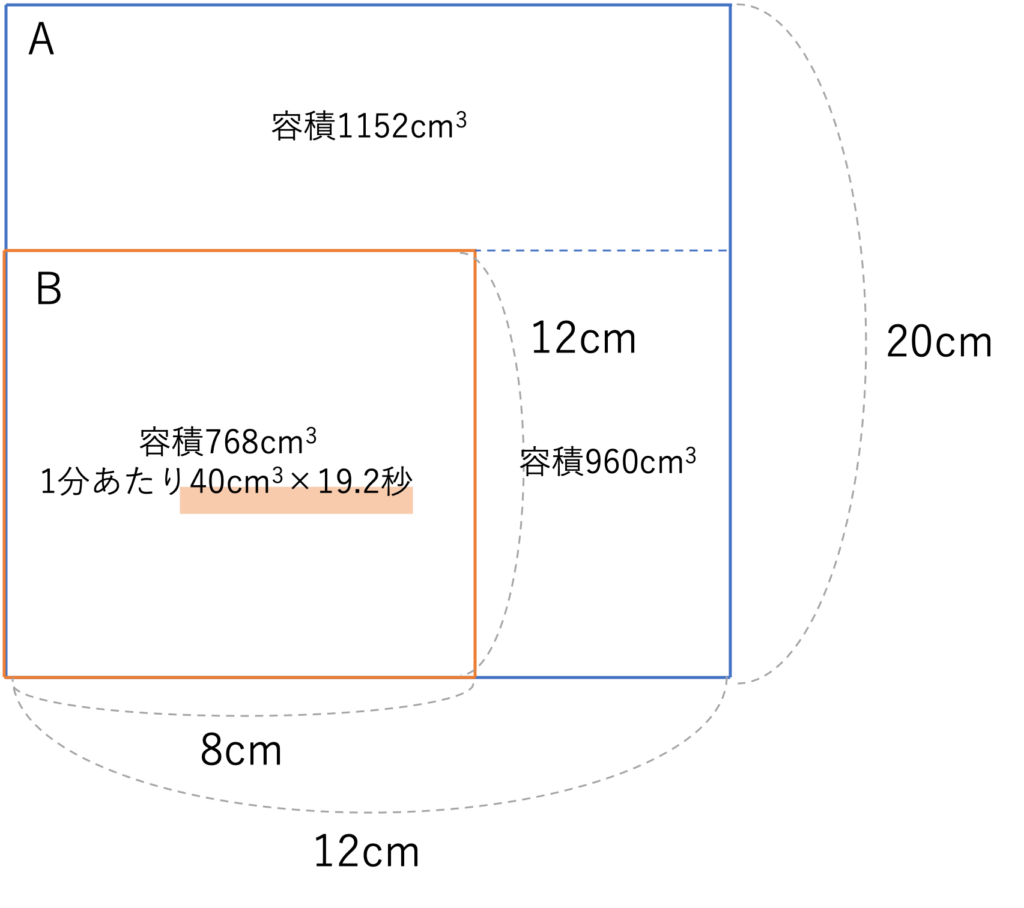
このことから22秒後、つまり容器Aに112cm3の水が入るときの水面の高さは12cmのところまでで収まるとわかります。したがってあとは112cm3という水の量を底面積で割って高さを出してあげれば、その値が答えとなりますね。いまこの部分の底面積は先ほど計算したように80cm2となりますので、112cm3÷80cm2=1.4cmとなります。
A.(3)1.4cm
このように平面図を書いてあげることで、少し奥行きが分かりづらくなるというデメリットこそあるものの、底面積や転換点が分かりやすくなります。今回の問題ではグラフは登場しませんでしたが、このような変化を捉えるというのはグラフありの問題と同じです。その点で基礎の重要さを再確認していただけますと幸いです。
問題② 排水が登場する問題!
続いては排水が関わる問題を確認していきましょう。水を入れる工程を給水、抜く工程を排水と一般に言いますが、受験問題ではこの両方が絡む問題がときに登場します。しかしそのような問題でも攻略法は変わりません。次に引用する問題は排水が関わる代わりに図形が簡単な長方形ですので、気負わず進めてみましょう。
図のような水そうがあり、毎分一定の割合でA管は水そうに水を入れ、B管とC管は水そうから水を出します。はじめにA管を開け、次にB管を開け、最後にC管を開けました。B管とC管が同じ時間に水を出す量の比は1:5です。グラフは、水槽の中の水の量と時間の関係を表したものです。このとき、下の問いに答えなさい。
(1)A管は毎分何Lの割合で水を入れていますか。
(2)□に当てはまる数はいくつですか。

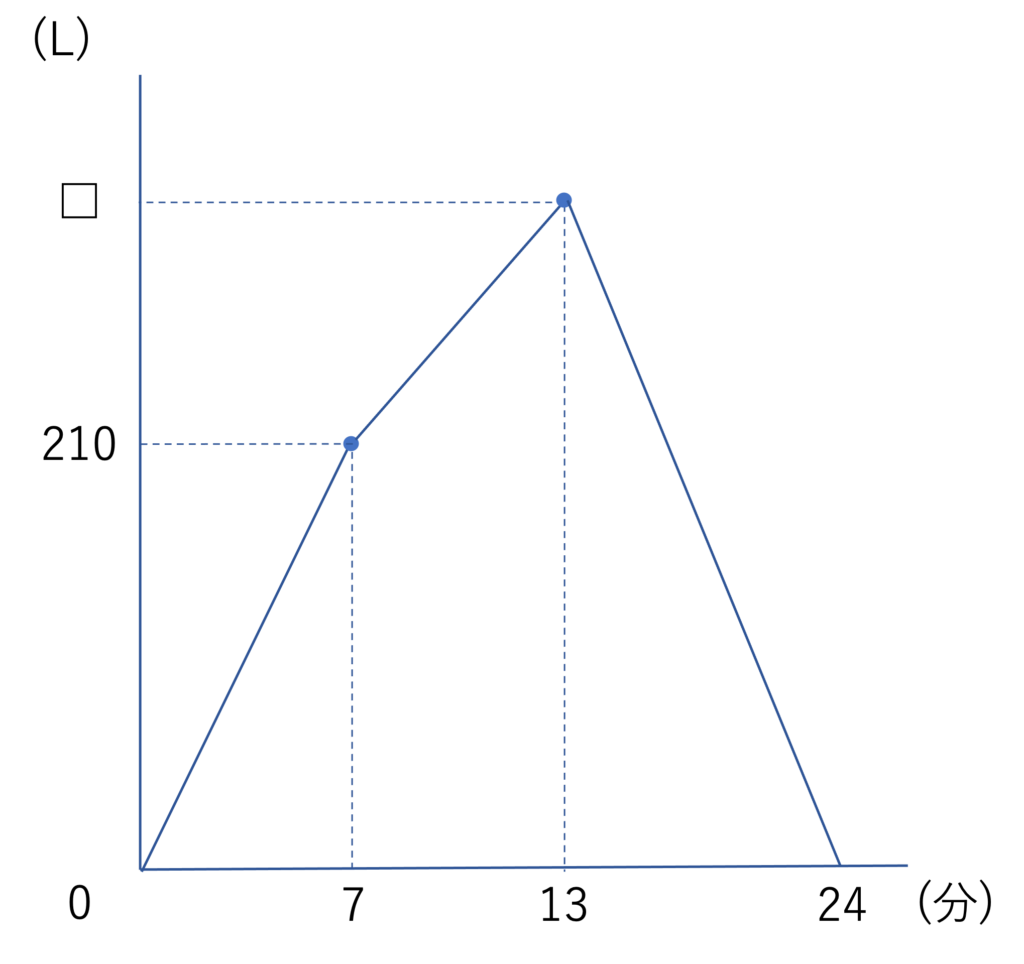
(八雲学園中学校(2018)、一部改題)
解説②
それでは2問目の解説を行なっていきます。この問題では先ほどご紹介した通り、水の給水と排水が関連しています。そのため慣れないとどうやって解けばいいのかわからないかもしれませんが、上の問題と同様に原則にしたがって解き進めていきましょう。ここで本当ならまず立体を平面に置き換えることから始めていきますが、今回の問題は図形がシンプルな直方体のため、あえてもう一回図を作る必要はありませんね。平面に起こすのは図形のおける底面積や高さの関係、およびそこから考える水の貯まるペースが分かりづらくなるからですが、図形がシンプルであればイメージが十分つきやすいです。飛ばせるところは飛ばしてスムーズに問題を終わらせましょう。
ということで、続いてペースの転換を押さえていきます。問題文をよく見ると途中でB管を開けその後にC管を開けているので、①A管のみ開く→②A管とB管を開く→③A管とB管をとC管を開くという3つのペースが登場することが分かります。ここで給水と排水の量の差と、それによる水位の変化について考えてみると、当然ですが給水量が排水量より多いと水は貯まり、それらが等しいと水の高さは変わらず、排水量が多いと水は減っていきますよね。

以上の関係からこのグラフを見ると、7分までの間は給水量が多く、7分から13分までの間は少しペースが落ちるものの給水量がなお多く、13分から24分にかけては排水量が多いということが分かります。この情報と先ほどの3つのペースが登場するということをまとめると、次のように中身を整理することができます。このように細かい中身を見ずともグラフの大まかな形から得られる情報は多いので、解く際はまずざっくり眺めていくことをオススメします。
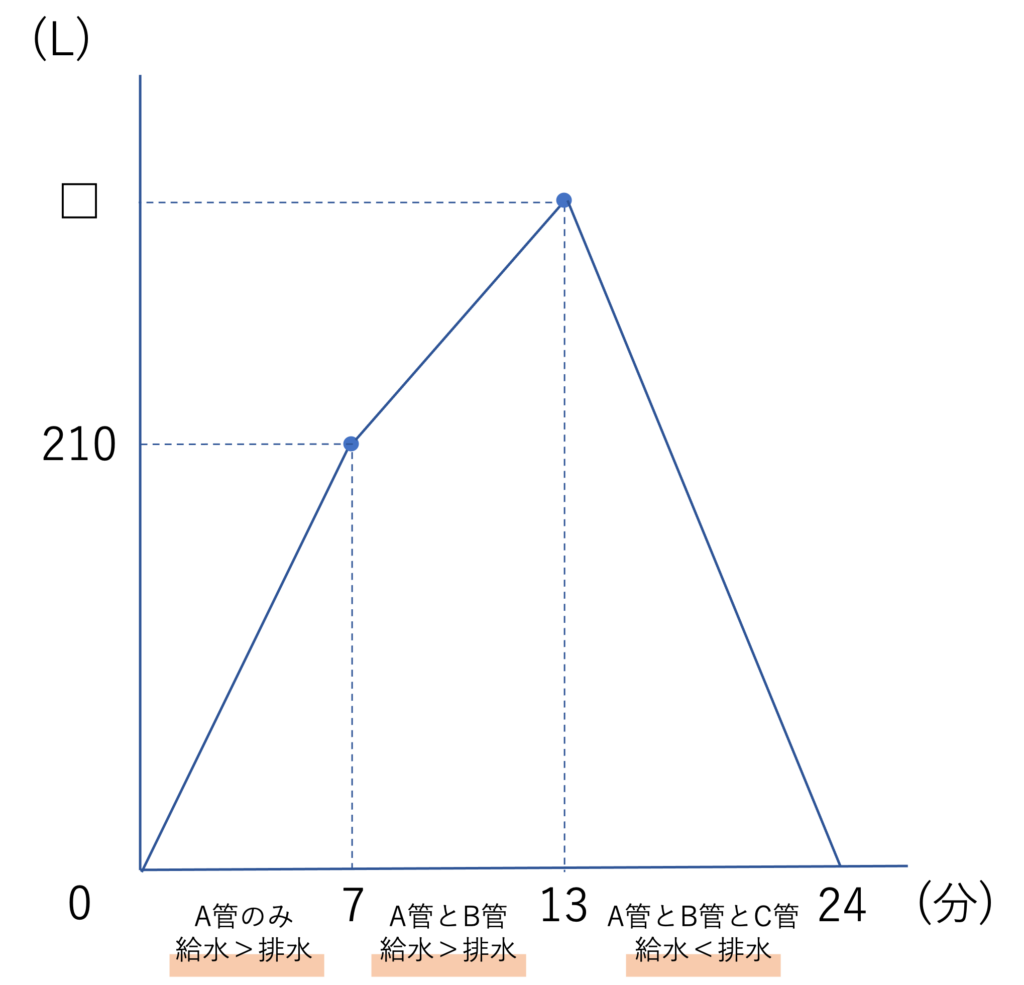
さてここで(1)の本題たる、Aの給水ペースにいて考えていきましょう。いま開始から7分間まではA管しか動いていないわけですが、この7分間で水は210L貯まっていることがグラフから判断できます。ここでそれぞれの管から水が入れる、または出す速度は一定なので、Aは毎分210÷7=30Lのペースで水を入れていると計算できます。
A.(1)毎分30L
さてこの調子で2問目に移りましょう。今度は□の中身、つまりは13分までで何L貯まったかを考えていきます。ここで再度問題文を見ておくと、B管とC管が同じ時間に水を出す量の比は1:5という情報が未だ使えていませんでしたね。問題文に使わない情報は登場しないので、この文章よりB管が1分間に○L水を出すとおき、C管をその5倍のペースである1分間に5×○Lのペースで水を出すとし、図に書き加えていきましょう。

ここで上のグラフのペースの転換点と、そのときの給水量と排水量の関係に再度注目していきましょう。先ほど見た7分までの間はA管飲みが開いていましたが、7分から13分の間はA管とB管が開いていますね。このとき給水量の方が排水量より多いことがグラフの形からわかっていますが、この区間では1分あたりに30Lの水が入り、それより少ない量である○Lの水が抜けていることが明らかになっているので、その差である(30-○)Lが1分あたりに貯まり、この6分間で6×(30-○)L=(180-6×○)Lが貯まっていくことが分かります。これと同様のことを13分から24分の間でも考えると、排水量の方が多いことから、この区間では1分あたりに水そうから(5×○+○-30)=(6×○-30)Lが出ていくことが計算でき、それが11分間続くので全部で11×(6×○-30)=(66×○-330)L抜けていくと判断できますね。
以上の計算をもとにすると□の中身を考えることができます。この量は0分から7分まで、および7分から13分までで貯まった水の合計である210+(180-6×○)=(390-6×○)Lを指し、同時に13分から24分までで抜けていった水の合計である(66×○-330)Lでもあります。このように1つの数字が2つのパターンで表されることを考えると次のような式を立てることができます。
390-6×○=66×○-330
72×○=720
○=10
いま○はB管から1分あたりに出ていく水の量を示す記号だったので、B管からは1分あたり10L、そしてその5倍の量が出ていくC管からは1分あたり5×10=50Lが抜けていくと判断できます。さて今回求めるのは□の値なので、上の式より□=390-6×○=390-6×10=330Lと計算できることから、答えは330となります。
A.(2)330
このように水の給水と排水が関わる問題では、そのどちらが多いのかを考えることで答えに辿り着くことができます。上の図でもご紹介した<、=、>の関係を覚えておくといいでしょう。
問題③ 複雑な立体の排水問題!
それでは最後に1問目と2問目が混ざった、複雑かつ給水と排水が関わる問題にチャレンジしていきましょう。初見ではなかなか解きづらいような問題ですが、2つの問題で使ったテクニックを合わせれば無事答えに辿り着けるでしょう。めげずにチャレンジしていただけますと幸いです。
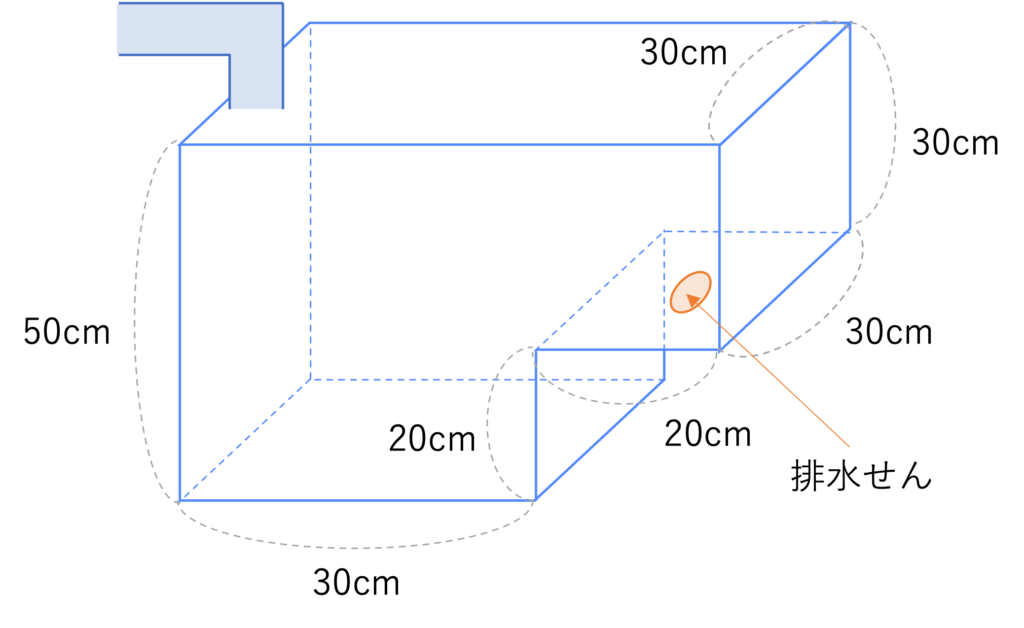
図のように、直方体を組み合わせた形の水そうに、排水せんが取り付けてあります。最初、排水せんは閉じられていました。この水そうに一定の割合で水を入れ始めてから10分後に誤って排水せんを開けてしまいましたが、気づかずに満水になるまで水を入れ続けました。下のグラフは水面の高さと水を入れ始めてからの時間の関係を表したものです。次の各問いに答えなさい。
(1)水そうに毎分何cm3の割合で水を入れましたか。
(2)水を入れ始めてから10分後の水面の高さは何cmですか。
(3)排水せんからは毎分何cm3の割合で水が流れ出しましたか。
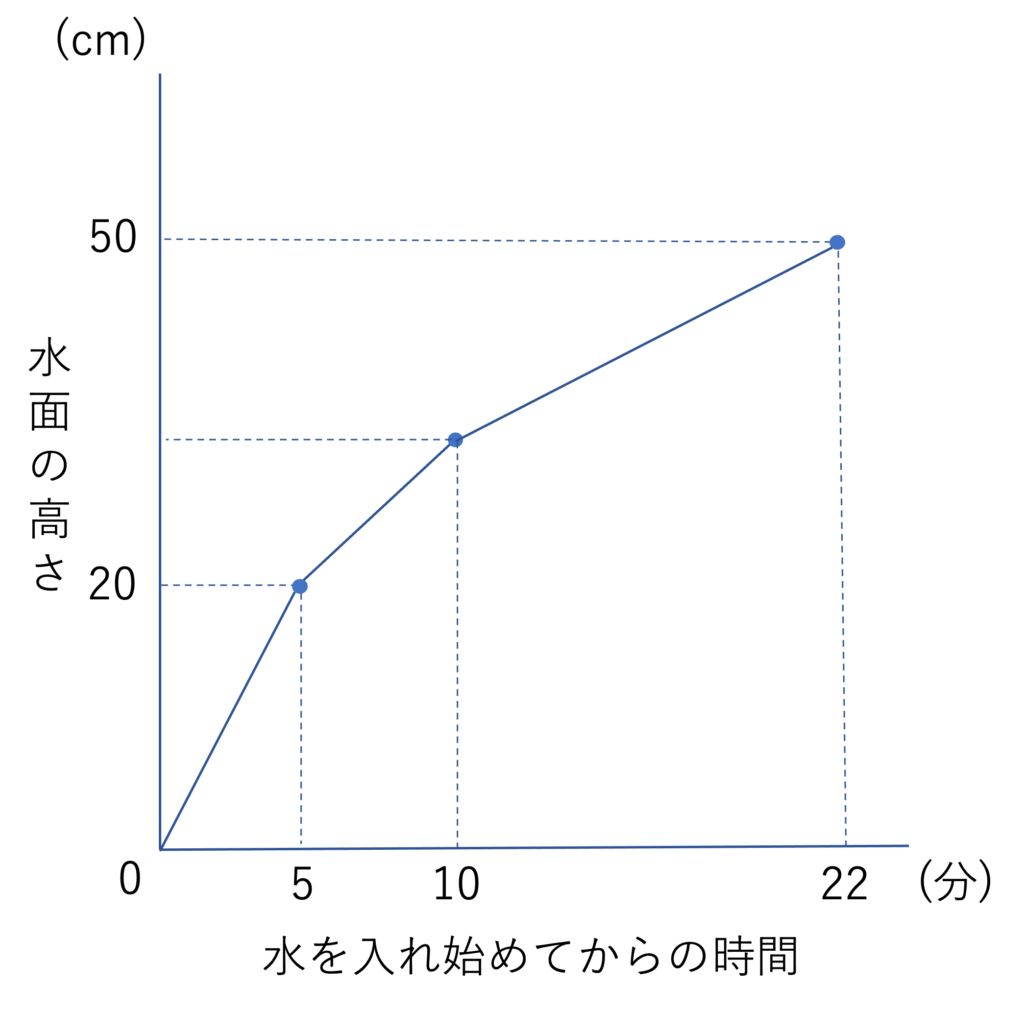
(山脇学園中学校(2021)、一部改題)
解説③
ここからは解説に移ります。細かいポイントは上の2つの問題で紹介したものと被るところがありますので、できるだけ簡潔にまとめていこうと思います。まずは定番の平面への置き換えですね。奥行きが30cmであることと排水線があることに注意して図を書いてみましょう。
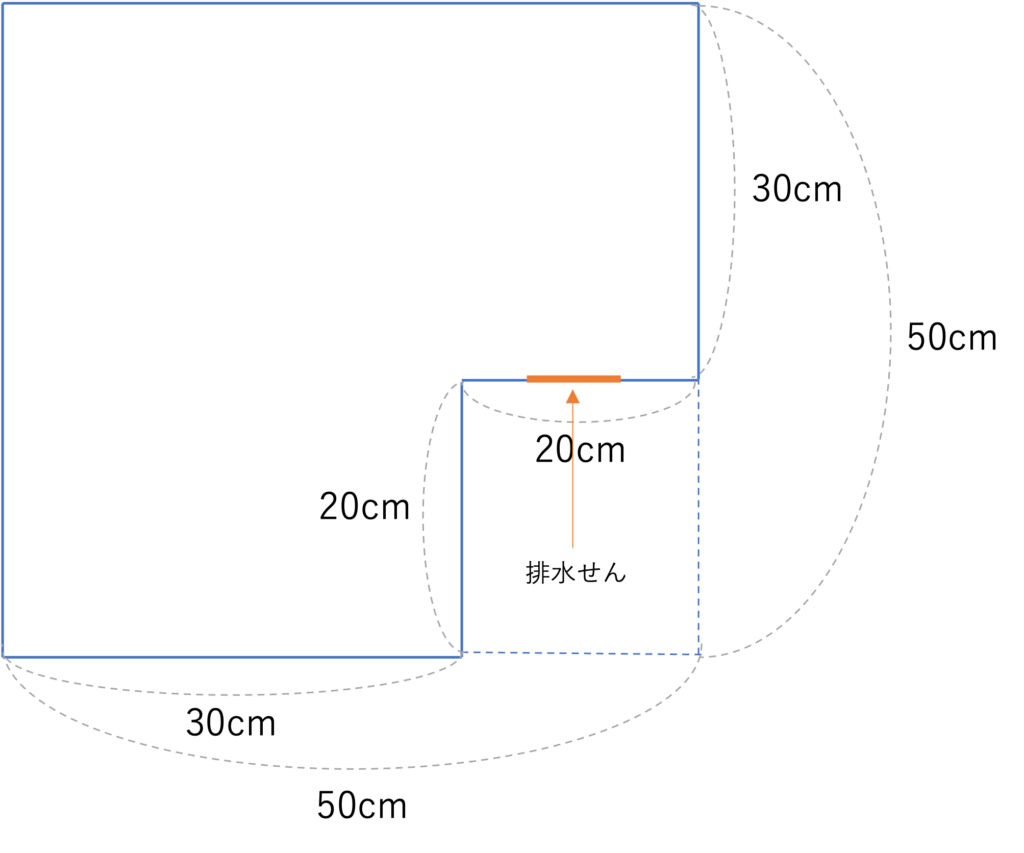
続いてはペースの転換の確認です。問題のグラフは2回折れ曲がっていて3つの直線から構成されています。ということは3通りの給水ペースが存在するということが判断できますね。実際問題を見ると、最初に入れているときのペース・10分後に排水せんを開けたときのペース、それから平面図より高さが20cmを超えたときのペースの3通りが存在することが分かります。ただしこの段階では排水せんを開けるのが先か、それとも20cmを超えるのが先かはまだ分かりません。しかし、ここで排水せんが20cmの高さの位置にあることに少し注目してみましょう。いま20cmに達しない段階で排水せんが空いてしまったら、20cmを超えた時点で給水量と排水量の差によって水が貯まっていくわけですが、このペースのまま満水になるまで水を流し続ける・抜き続けることになることからペースは2つしか存在しないことになってしまいます。これだと上の説明と食い違ってしまいますので、このことから20cmに達するのが先で、その後排水せんが空くことが分かりますね。このような蛇口や排水せんの位置などでも読み取れる情報があるので、注意する癖をつけておくといいでしょう。
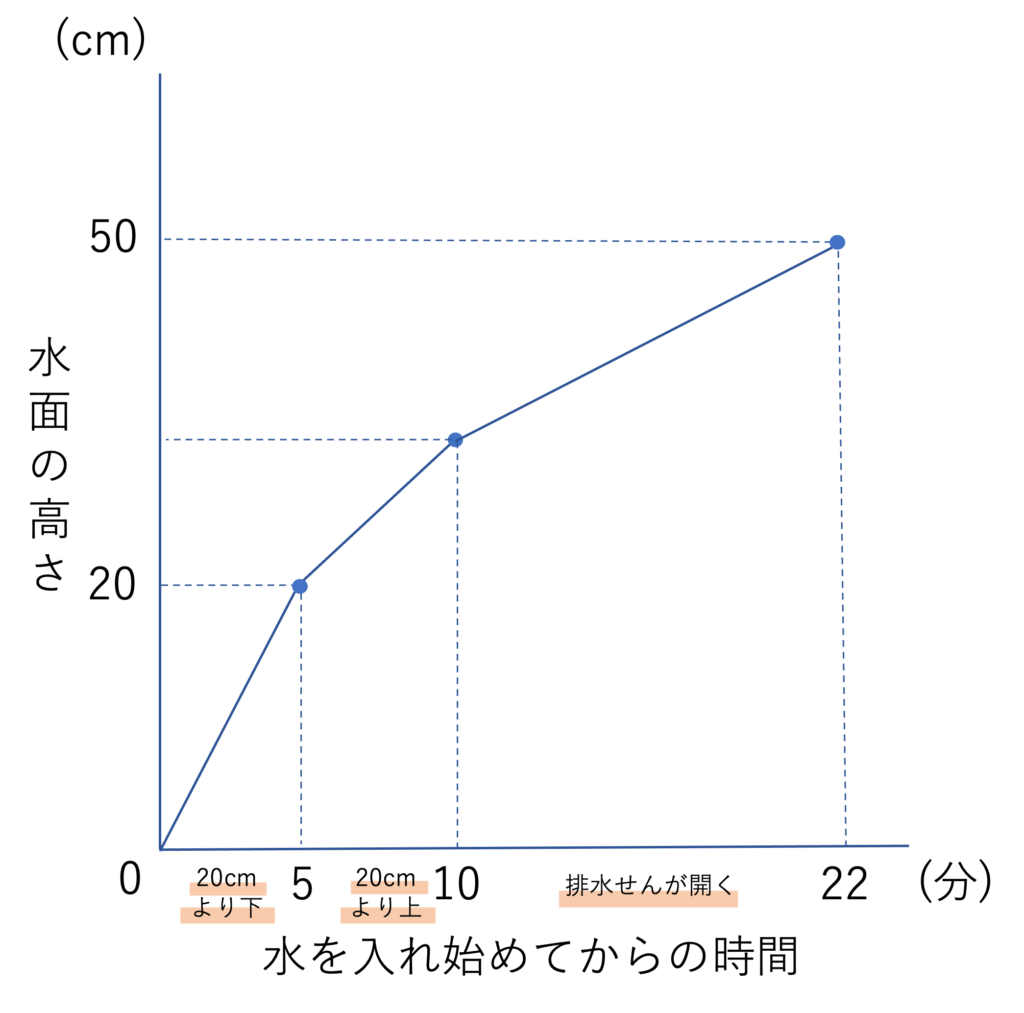
さてここまで問題文の中身を整理してきましたが、ここから本題の設問に入っていきましょう。まずは1分あたりに入れる水の量ですね。ここではグラフ中の、5分後までで20cmの水位まで貯まったことに注目していきます。上の図形の形から、20cmの部分までの容積は30cm×30cm×20cm=18000cm3だと分かります。いま5分間でこの部分に水が入り切ることから、1分間には18000cm3÷5分=3600cm3の水が流れることと計算でき、したがって答えは毎分3600cm3となります。
A.(1)毎分3600cm3
続いて10分後の水面の高さについて考えていきましょう。ここで(1)の内容より、5分後までで20cmの部分は水で埋まりきっていることが分かっています。この情報をまとめると下図のように整理することができます。
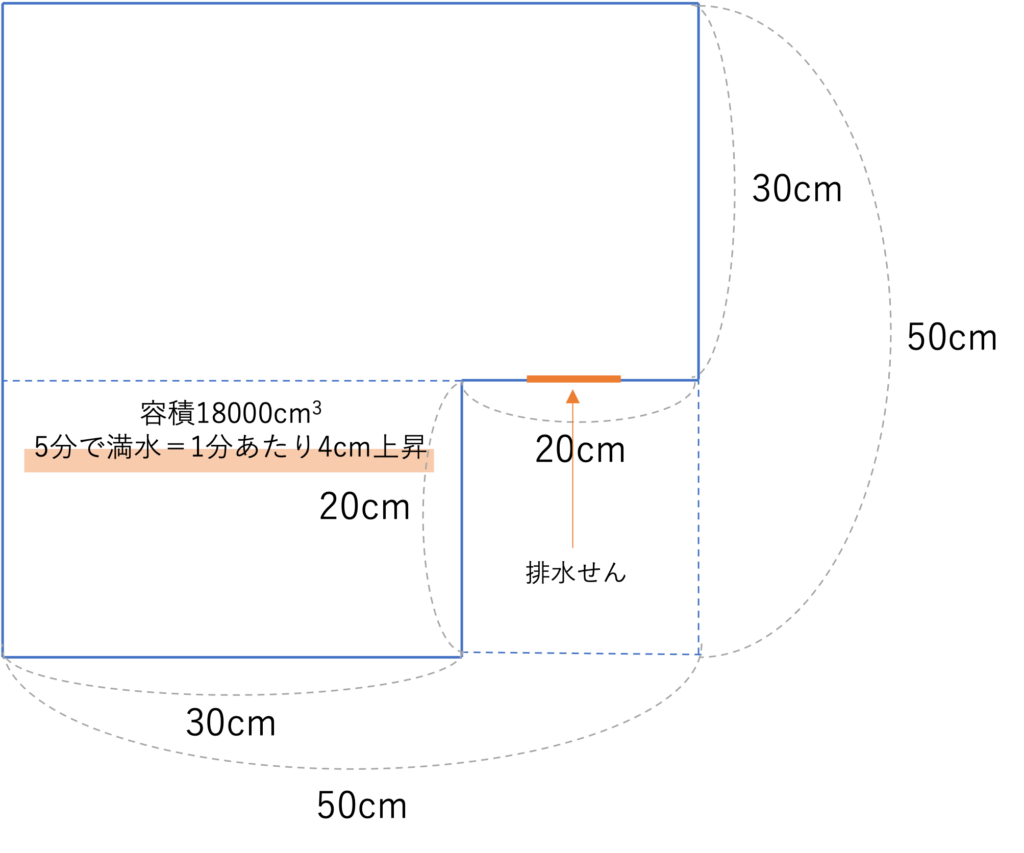
さて5分後までで20cmの部分まで貯まることが分かっているので、5分後から10分後までの5分間でどれくらいまで水が貯まるのかを考えていけばいいですね。水が入るペースは(1)で計算したように毎分3600cm3なので、5分間で3600cm3×5=18000cm3の水が水そうの中に流れていくわけですね。ここで20cmより上の部分の立体の形に注目すると、この部分は20cm以下の部分より底面積が大きくなっており、その値は50×30=1500cm2となっていることが分かります。ここで上昇する水位を求めるには貯まる水の量を底面積で割ってあげればいいので、上で求めた計算の結果より18000cm3÷1500cm2=12cmが5分間で上昇することが分かります。そして前述したように5分後までで20cmまで溜まっていることと合わせると、答えは20cm+12cm=32cmとなります。
A.(2)32cm
さて(2)までで、排水せんが開く10分後までの間に32cmの部分まで水が貯まるということを求められました。それゆえ1分あたりに排水せんから流れる水の量を計算するには、10分後から水位の変化がどうなるかを追っていけばいいですね。ここでグラフの形に注目すると、10分後からグラフの傾き、つまりは貯まっていくペースが遅くなり、22分後までの12分で満杯になることが分かります。満杯のラインは高さ50cmにあるので、10分後までで32cmの高さに達したことを考えると、12分間で18cm分の水が貯まるようであればいいことが分かります。
ここで18cm分の立体の容積について考えると、底面積が(2)で見たように1500cm2であったことから、1500cm2×18cm=27000cm3だと計算できます。12分間でこの量が水そうに貯まればいいので割り算すると、1分あたりに27000cm3÷12=2250cm3のペースであればいいと判断できます。しかし水が入るペースは(1)より3600cm3だと導かれていました。つまりその差の量が排水せんから流れていればいいわけですね。(2)でも確認したように給水量が排水量より多いとき、貯まる量はその差になりますので、それゆえ今回の問題において排水せんから流れる水の量は3600cm3-2250cm3=1350cm3となります。
A.(3)毎分1350cm3
このようにやや複雑そうに見える長い問題でも、基礎的な攻略法を徹底して実践していけば無事解き終えることができます。特に今回の問題は平面図・転換点という2つのポイントについてじっくり考えなければならない問題であり受験でも登場しやすい形ですので、この問題を自力で解けるようになる程度のレベルを目指して勉強していくといいでしょう。
終わりに
今回の記事では水量変化とグラフという範囲に焦点を当て、その実践的な解き方をご紹介していくものでした。最初に触れたように、この問題はシチュエーションが細かく文章も長く情報量も多く苦戦しやすいでしょうが、パターンそのものは意外と少ないため基礎力がついていれば解き切ることができます。したがって本番に向け、オススメ記事や参考書だけを使いながら更なる対策を行なっていきましょう。本記事が今後の学習の甥役に立てば幸いです。