問題
下の図のように、円と4つの直角三角形が重なっています。円の周の長さが25.12cmであるとき、ぬりつぶした部分の面積の合計は□㎠です。ただし、同じ印のついた辺は同じ長さとします。
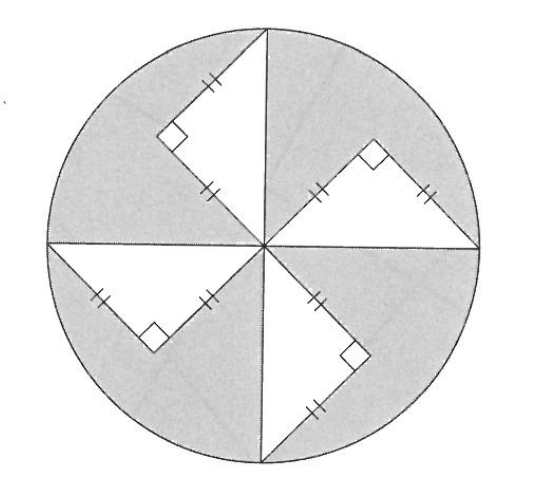
解説
円周が25.12cmと分かっているので、円の半径を⚪︎cmとすると、
\(⚪︎ \times 2 \times 3.14=25.12\)
\(⚪︎=25.12 \div 3.14 \div 2\)
\(=4\)
より、4cmとわかります。
また、4つの直角二等辺三角形を上手に移動させると、対角線の長さが4cmの正方形2つ分に変形でるので、これらの面積を求めると、
\(4 \times 4 \div 2 \times 2=16\)
より、16㎠とわかります。(正方形の面積=対角線×対角線÷2はよく使うの覚えておきましょう)
以上から、塗りつぶした部分の面積は、
\(4 \times 4 \times 3.14-16=34.24\)
より、34.24㎠となります。
答え:□=34.24
おすすめ記事
- 補助線の引き方のコツ
- 等積変形・等積移動とは?頻出の問題と苦手な子でもわかる考え方を紹介
- 等積変形の利用~ヒポクラテスの月~
- 円とおうぎ形の周りの長さ、面積の求め方
- おうぎ形の面積に関する標準問題3選
- おうぎ形に関する応用問題3選!
参考