今回の記事では,多角形の性質について解説していくシリーズの第2本目として,実際に入試に登場した問題を引用しながら応用的な知識や攻略法をご紹介していきます。前回の記事でも申し上げましたが,図形の性質は基本的な知識であるだけに,覚えていないと周りと大きな差をつけられてしまいます。早いうちから覚えきってしまう意識を持ちながら,演習で取り組んでいただけますと幸いです。
Contents
多角形とは…?
では問題演習に移る前に,前回の基礎編で確認した多角形の基本的な性質について復習していきましょう。前の記事で重点を置いたのは,内角・外角・対角線の関係です。まず大前提として図形にはいくつかの頂点と辺が存在していて,それらの数に応じて呼び名が変わりますね。頂点と辺が3つなら三角形といったように,頂点と辺が○個ある図形のことは○角形と呼ばれます。この○の中身と内角・外角・対角線の関係を前回は見ていったのでした。
性質の詳細やなぜそのようなことがいえるのかという説明は以前の記事を振り返っていただくとして,ここで大まかな説明をしておきましょう。まず○角形の内角の和は180°×(○-2)で計算することができます。他方外角については図形がどんな形であろうと360°になります。まずはこれらの内角と外角の2つの要素や関係を頭に入れておきましょう。また前回は対角線の本数についても見ていきましたね。○角形の対角線の本数は(○-2)×○÷2(本)になります。これらの3要素が平面図系の問題を解く上では非常に重要になってきます。今回ご紹介する問題でも使うことができる関係ですので,ぜひ頭に入れておいてください。
問題① 基本的な問題で知識を振り返ろう!
それではここからは本題の問題演習に移りましょう。まずは基本的な角度の問題です。この問題は主に三角形の性質を使うことで解くことができる問題ですので,ミスがないように答えを導いてみましょう。
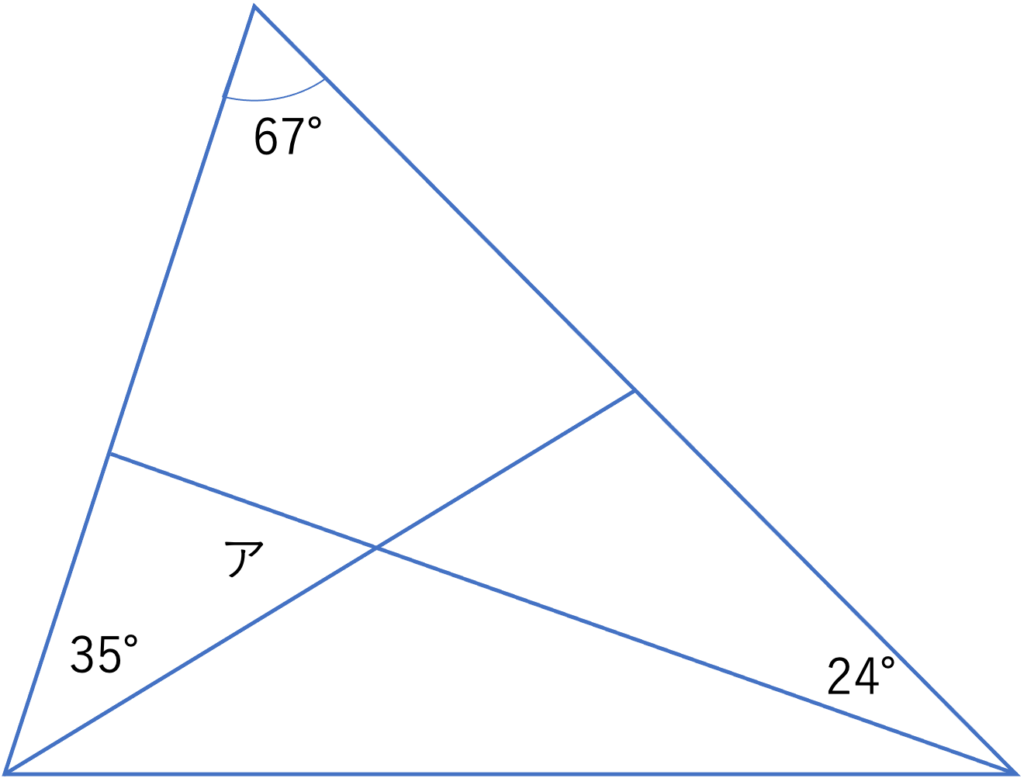
下の図において,アの角度を求めなさい。
(埼玉栄中学校(2018),一部改題)
解説①
それではここからは解説を行なっていきます。答えが出せた・出せなかった,正解した・しなかったにかかわらず,参考にしていただけますと幸いです。まず今回の問題ですが,三角形の中に2本の線が引かれており,その中に存在する角度の大きさを求めるという構造になっています。このように図形の内部に線が引かれているときはその線に沿って図形を切り分けたり,また切り分けた図形を組み合わせたりしながら,少しずつ角度を埋めていくことが大切になってきます。今回の問題でも67°・24°・35°という3要素からアの角度をいきなり求めるのは難しいので,まずは下の図のように,上の大きな三角形の中に存在する2つの三角形に注目していきましょう。
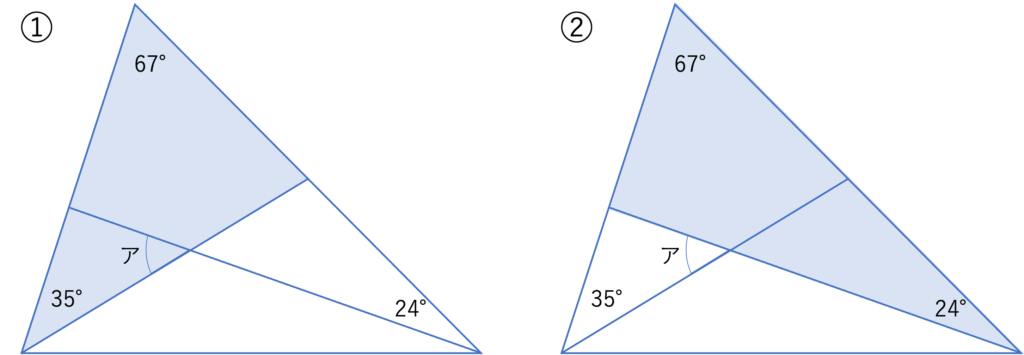
今回の三角形には上のような2つの三角形が存在することがわかりますね。これらの三角形の他にも考えられる図形はたくさんありますが,その中でも答えを求める上で有効な図形を見つけ出すポイントとしては,1つだけ角度がわからない図形を作り出すことです。上の①と②の図形だと,三角形のお尻に相当する部分の角度だけが明らかになっていませんよね。このように1つだけ角度がわからない図形は,他の角度と内角の和の関係から角度を計算することができ,情報を増やすことができるので大変有益です。例えば①だと三角形の内角の和は180°であり,3つの角度のうち2つの角度の合計が67°+35°=102°なので,180°-102°=78°だということが分かります。同じ要領で②についても考えると,大きさが分かっている2つの角度の合計が67°+24°=91°なので,残りの1つの角度は180°-91°=89°だと分かります。
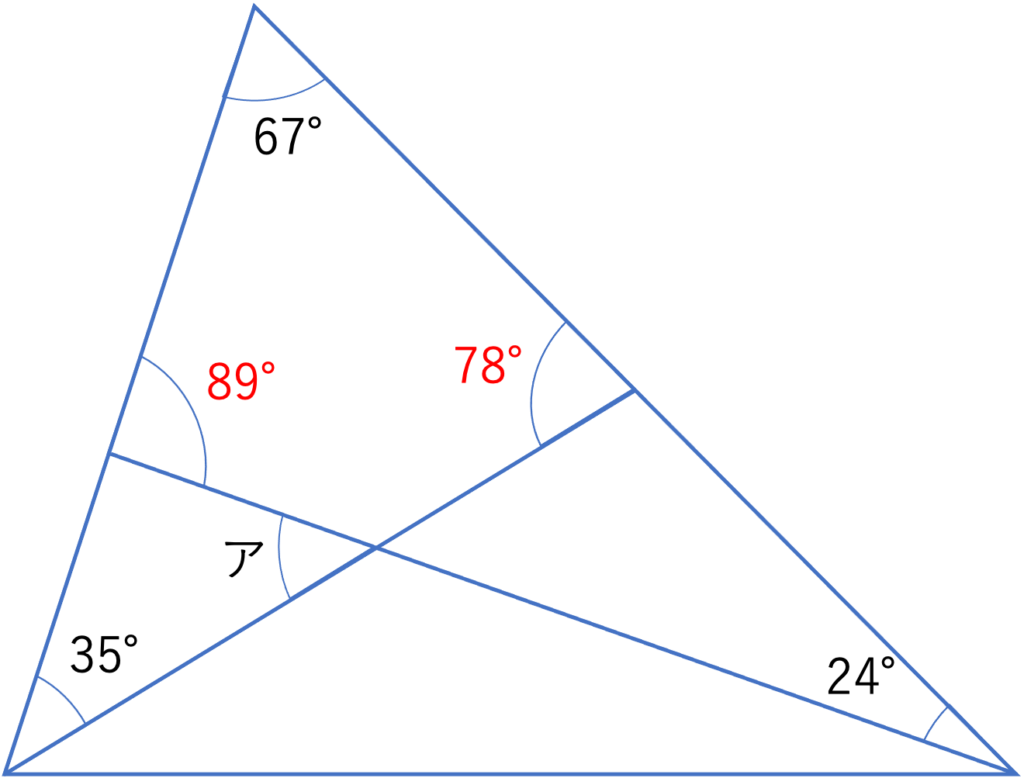
そしてまた1つだけわからない角度が存在する図形を作り出していく,という原則に則って問題を進めていきましょう。次に考えられるのは下の図のような四角形になります。この図形は分からない1つの角がアの反対側に存在するため,答えを求める大きな手がかりになると考えられます。どの角度が答えを求めるべき場所に近いかという要素は答えを計算する上で意識しておくといいでしょう。
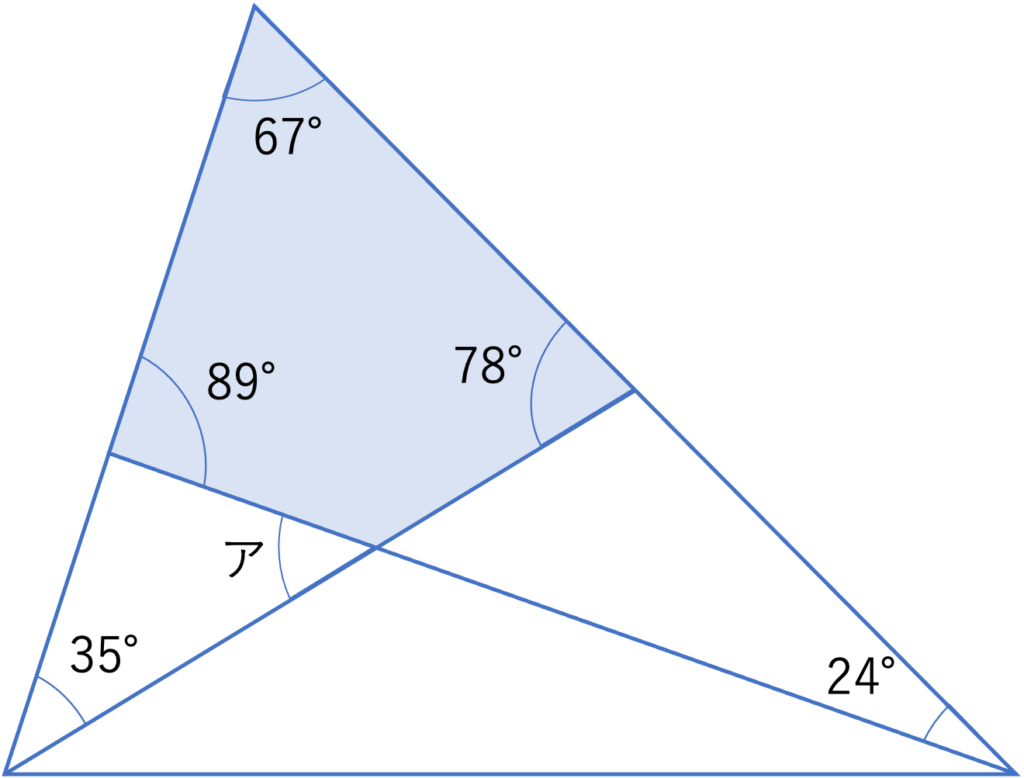
この四角形では67°・78°・89°という3つの角度の情報が与えられています。そして四角形の内角の和は360°なので,360°-(67°+78°+89°)=360°-234°=126°という計算から残った1つの角度が126°だと計算できますね。

そして上の図からもわかる通り,この126°という角度はアの反対側に存在するため,180°-126°=54°という計算から,答えとなるアの角度は54°になります。このように図形を作り出し,内角や直線状の角度の関係を活かしながら計算を進めていくことが多角形の性質に関する問題では重要となりますので,ぜひ参考にしてみてください。
A.54°
問題② 情報の少ない問題に挑んでみよう!
続いては六角形に関する問題です。この問題では前回の記事でご紹介した公式をうまく使うことができるでしょう。ぜひ覚えた知識を活かすようなイメージで解いてみてください。
下の図は正六角形です。角xの大きさは何度ですか。
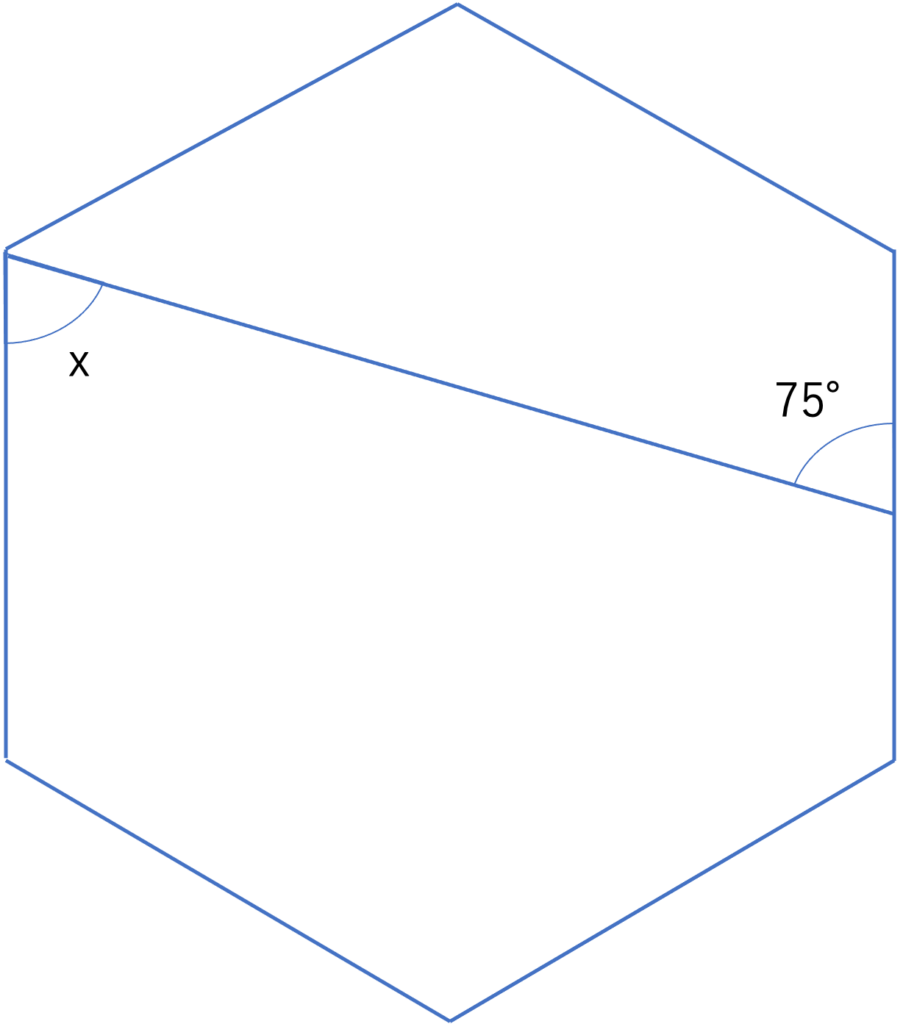
(横浜女学院中学校(2021),一部改題)
解説②
では2問目の解説をしていきます。この問題は正六角形の中に1本線分が引かれており,その線分を基準として,角度の大きさを求めていくというものになっています。今回は与えられている情報が少なめですが,正六角形という言葉が見受けられるため,そのワードをもとに情報を増やしていきましょう。この正六角形と言う条件から得られる情報には,まず内角の和が挙げられますね。上でも確認しましたが,180°×(6-2)=180°×4=720°という計算から,内角の和は720°だと判断できます。続いて内角の和から,それぞれの角度の大きさも求めることができますね。6つの角度がそれぞれ等しく合計すると720°ということは,その和を6等分すればいいわけです。それゆえ1つの角度の大きさは720°÷6=120°となります。このように正○角形という言葉が存在するときは,その図形の内角の和だったりそれぞれの角の大きさだったりに着目して内容を深掘りしていくといいでしょう。ここまでの内容を整理すると下の図のようになります。
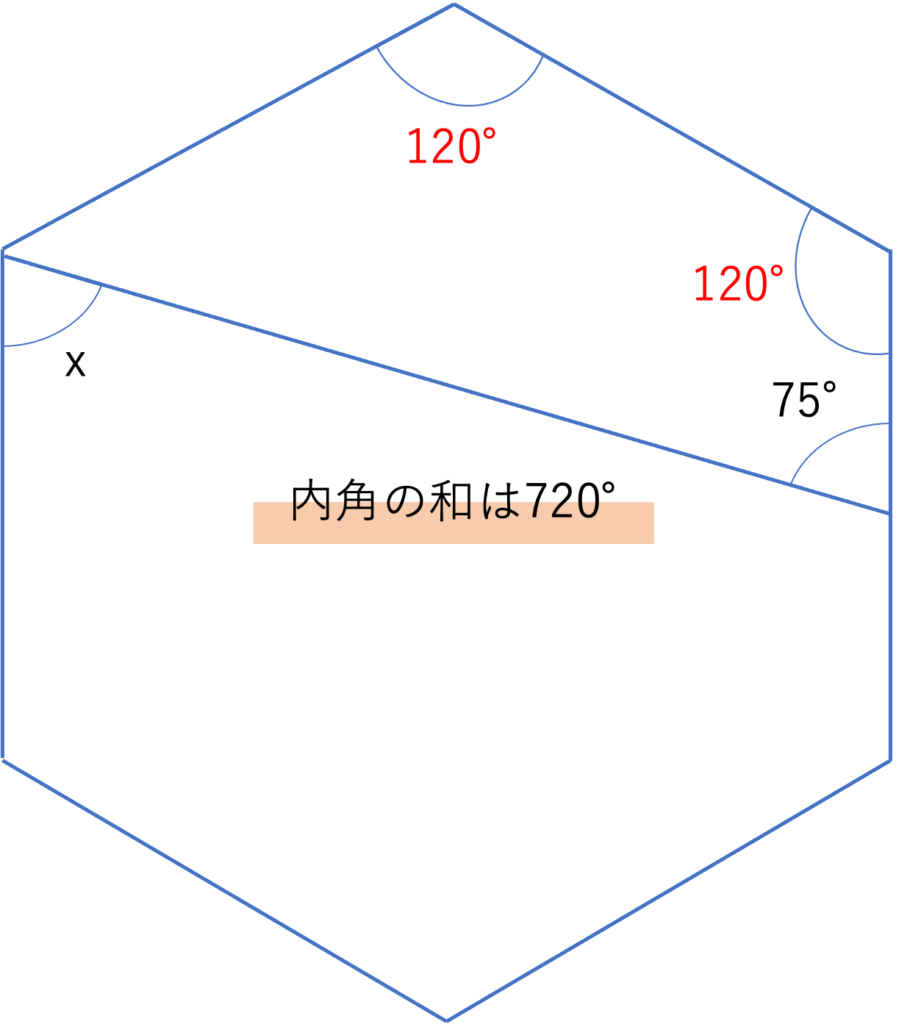
さてこの図に基づいてxの値を考えていくわけですが,ここで先ほど同様に1つだけ角度の値が分からない図形があるかどうかを考えていきましょう。今回だと六角形の上部に120°・120°・75°という3つの角度が分かっている四角形を作り出すことができますね。この図形の残りの1つの角度が内角において角xの反対側に存在するため,利用することで答えを求める上で必要となる情報を埋めていきましょう。ここで四角形の内角の和は360°なので,残りの1つの角は360°-(120°+120°+75°)=360°-315°=45°であることが分かります。

そして正六角形においてそれぞれの角度が120°であり,上の図から45°とxを足すと1つの内角が出来上がることを考えると,答えとなるxの大きさは120°-45°=75°であることが分かります。このように正○角形が問題の中に登場してきたら,その図形の性質や要素について考えた上で計算を進めていくといいでしょう。
A.75°
問題③ 見慣れない図形に多角形の性質を適用しよう!
続いての問題では見慣れない形の図形が登場します。やや癖があり解きづらいかもしれませんが,基礎編でご紹介した多角形の性質を使うと計算を簡略化できるので,どうやったら楽に答えが出せるかを考えながら進めていくといいでしょう。
下の図で,角xは何度ですか。
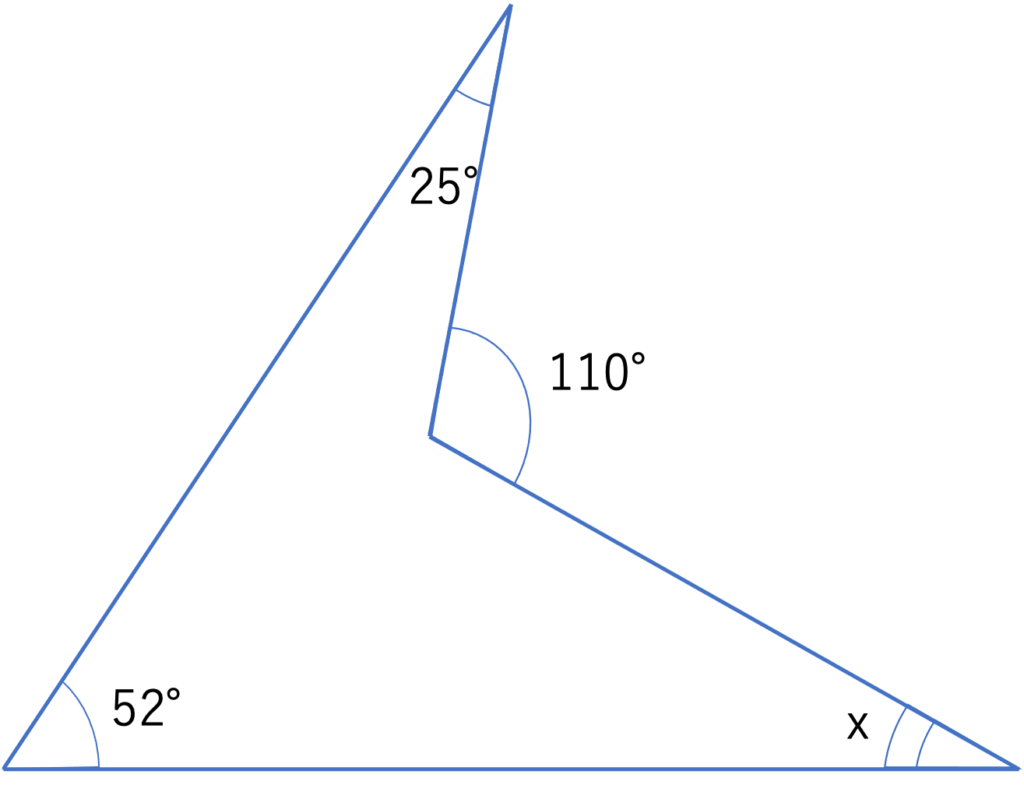
(足立学園中学校(2018),一部改題)
解説③
さてここからは解説に移ります。この問題で登場している図形はかなり歪な四角形ですね。分かっている角度も四角形の中の2つの内角と1つの外角ということで,情報はそれなりに揃っているように見えるものの,図形を切ったり組み合わせたりするという原則も1つだけ角度がわからない図形を探すという原則も使えないためどこから手をつけていけばいいのかが分かりづらいです。
このような場合は答えとの関連は気にせず分かりそうなところから順に埋めていくことをオススメします。例えば今回の問題だと,110°の角の反対側に存在する内角の大きさを求められそうですね。360°-110°=250°という計算から,この部分の角度は250°であると求められます。
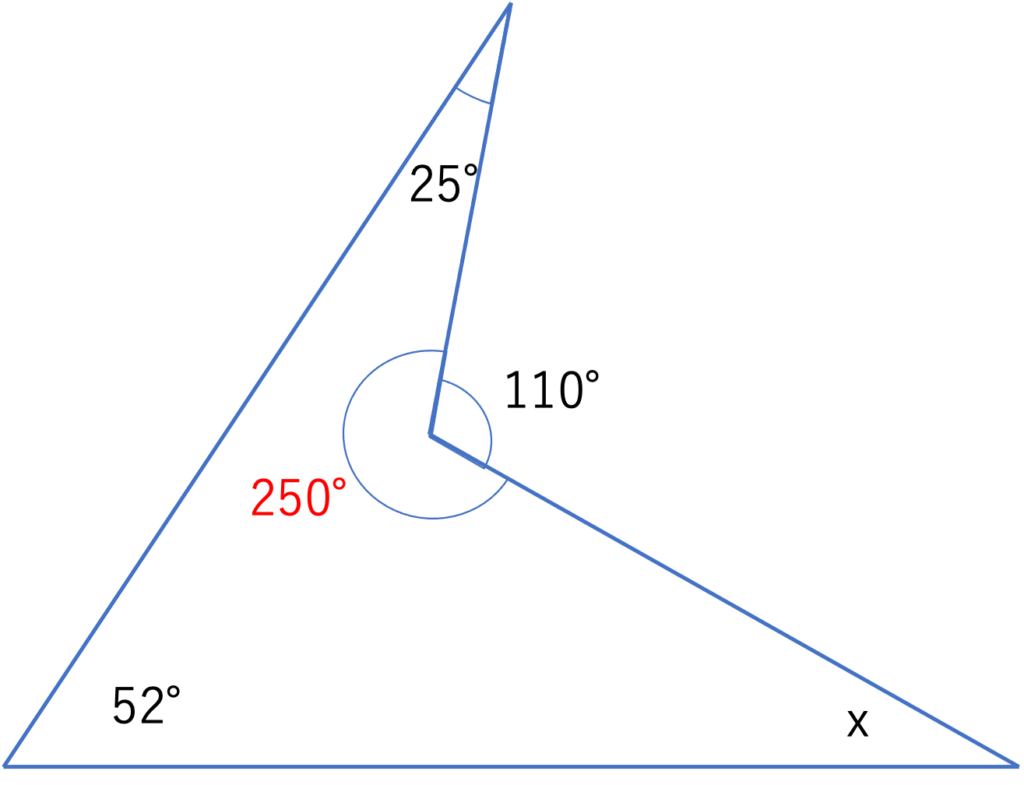
そしてこの部分の内角が求められたので,図の四角形のうち大きさがわからない角度が1つだけになりますね。このことから内角の和の大きさの関係を使って答えを求められそうです。四角形の内角の和は360°なので,xの大きさは360°-(25°+52°+250°)=360°-327°=33°となります。
A.33°
このように図形の形に見覚えがなくても,多角形の性質を当てはめることはできますし,その性質に基づいて手を動かしていけば無事答えを導くことができます。その点で原則や関係をきちんと頭に入れておくことの重要性を感じていただけますと幸いです。
問題④ 特殊な設定な問題に触れてみよう!
最後にご紹介するのは特殊な設定の問題です。特殊とは言っても三角定規というだけに過ぎないのですが,定規に代表されるような決まった形の三角形への理解がないと解きにくいかと思われます。もし不慣れなら調べながら進めてみてもいいでしょう。
下の図は,1組の三角定規を重ねたものです。このとき,角xの大きさは何度ですか。
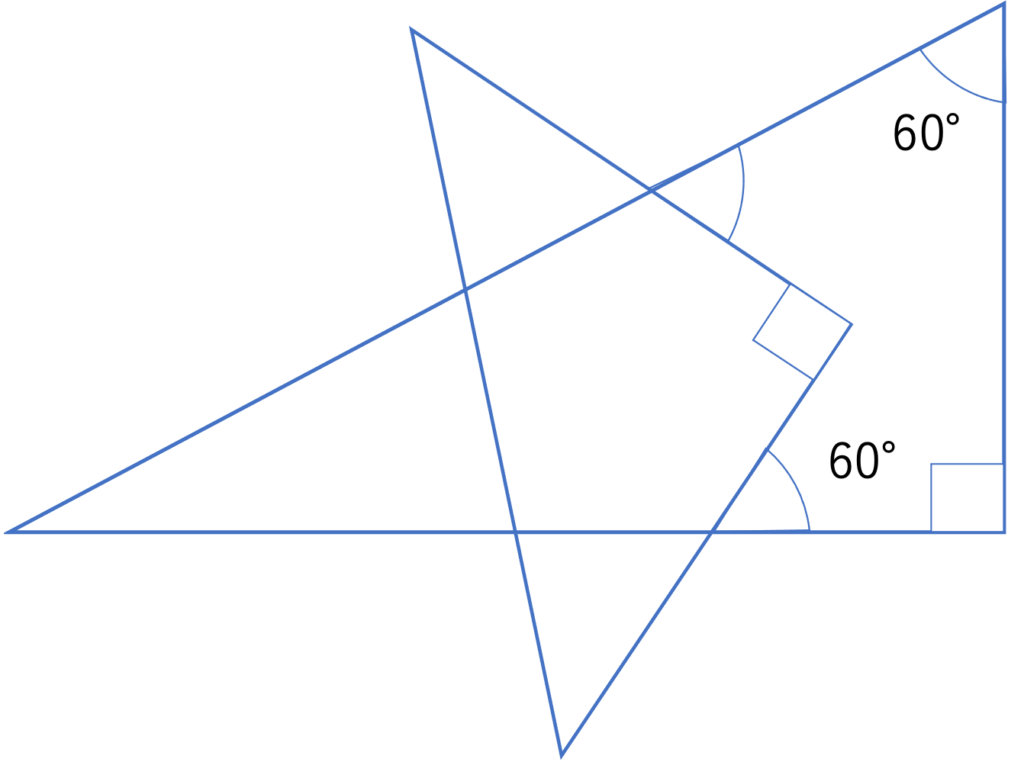
(東京家政大学付属女子中学校(2012),一部改題)
解説④
では最後の問題の解説を進めていきます。この問題は2組の三角定規を重ね合わせたときに出来上がる図形に関する問題でした。三角定規は45°・45°・90°という二等辺三角形と30°・60°・90°という三角形の2つで構成されているわけですが,これらの事柄を知っていないとなかなか解きづらいでしょう。しかし多角形の性質を使えば,三角定規の性質を使わなくても問題を解くことができます。
まずは3つ目の問題と同じように,求められそうな部分の角度の値を計算していきましょう。今回だと図形の中央に位置する,90°の反対側に存在する角度の大きさが計算できそうですね。360°-90°=270°であることから,下の図のように情報を埋めることができます。
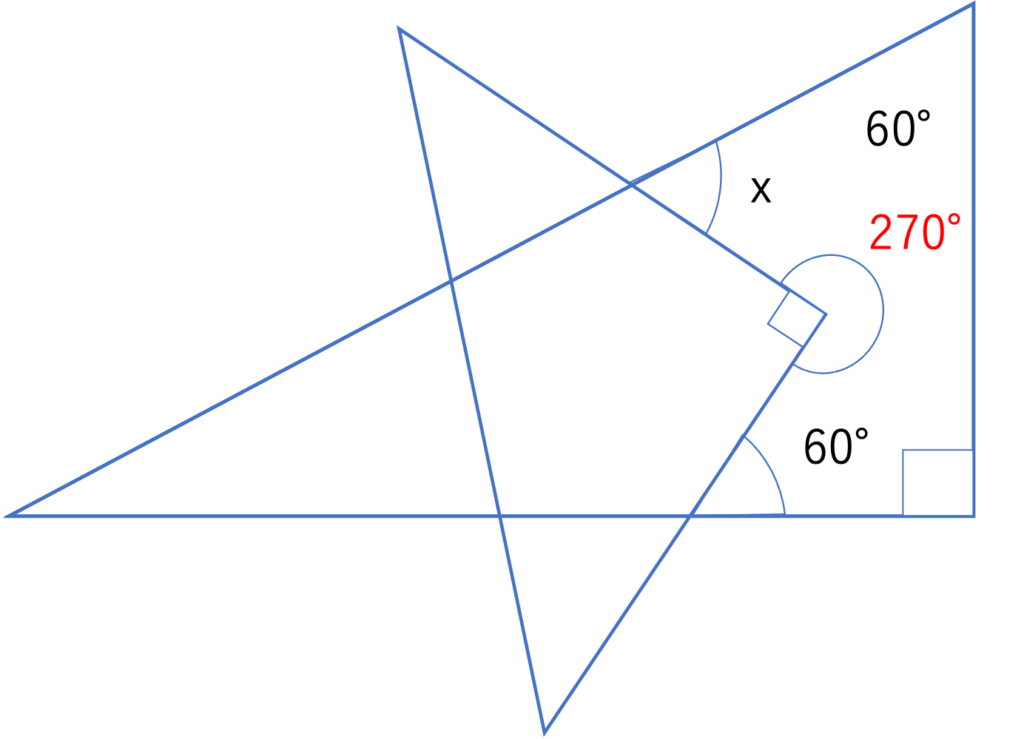
さて270°という情報を落とし込めましたが,ここで答えを求める上で重要なポイントである1つだけ角度の大きさのわからない図形への注目というものを思い出しましょう。今回の図形だと,60°・90°・60°・270°・xという5つの角度が存在するいびつな五角形が存在するので,その部分に注目して答えを導きましょう。内角の和の公式から,五角形の内角の和は180°×(5-2)=540°なので,540°-(60°+90°+60°+270°)=540°-480°=60°であると計算からxは60°であることが分かります。このことから答えは60°となります。このように公式や関係を把握しておくことは,ときに細かい知識不足をカバーすることや計算を簡略化することにつながるので,実践でも積極的に使ってみるといいでしょう。
A.60°
終わりに
今回の記事では多角形の性質に関するシリーズの応用編として,実際に受験で登場した問題を引用しながら応用的なテクニックについてご紹介していくものでした。この記事で取り上げた問題はほんの一部に過ぎませんが,どの問題にも適用可能なエッセンスを得ることはできるのではないでしょうか。よろしければ下のおすすめ記事や参考書籍を使いながら,知識の定着に励んでいきましょう。本記事が今後の学習のお役に立てば幸いです。
おすすめ記事
参考
- 粟根秀史,「中学入試 分野別集中レッスン 算数 平面図形(中学入試分野別集中レッスン)」,文英堂(2020/7/9)
- 粟根秀史,「中学入試 分野別集中レッスン 算数 立体図形(中学入試分野別集中レッスン)」,文英堂(2020/7/9)
- 小杉拓也,「増補改訂版 小学校6年分の算数が教えられるほどよくわかる」,ペレ出版(2020/7/4)