問題
下の図で、四角形ABCDは平行四辺形です。角xの大きさは□度です。ただし、同じ印のついた角は同じ大きさとします。
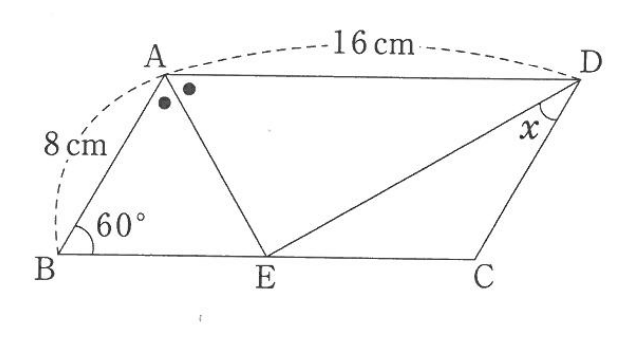
解説
問題の取っ掛かりとしては、特別な図形の性質(今回で言うと平行四辺形や正三角形、二等辺三角形など)や既に与えられている角度の情報(特別角であると30°、45°、60°、90°は頻出です)から、徐々に未知の角度を求めていく、というのが大まかな流れになります。
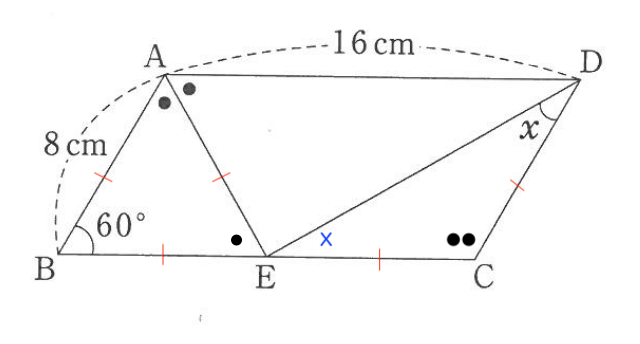
今、□ABCDは平行四辺形なので、
\(AD \parallel BC\)
となり、錯覚の性質から、
\(\angle{DAE}= \angle{BEA}\)
が成り立ちます。
この時、△ABEは全ての角が等しいことになるので、1辺の長さが8cmの正三角形であるとわかり、●1つ分の大きさが60°、ECの長さが8cmとわかります。
更に、平行四辺形の性質から、
\(\angle{BAD}=\angle{BCD}\)
\(AB=DC\)
であるので、△DCEは頂角が120°の二等辺三角形であるとわかります。
以上より、\(\angle{x}\)の大きさは、
\(x°+x°+120°=360°\)
\(x°=30°\)
となります。
答え:□=30
おすすめ記事
- 補助線の引き方のコツ
- 等積変形・等積移動とは?頻出の問題と苦手な子でもわかる考え方を紹介
- 等積変形の利用~ヒポクラテスの月~
- 円とおうぎ形の周りの長さ、面積の求め方
- おうぎ形の面積に関する標準問題3選
- おうぎ形に関する応用問題3選!