ばねの基本を理解する～自然長の意味とばねとばねにかかる力の比例関係～【中学受験理科】

皆さんはばねの問題でつまづいたという経験がありますか？日常のいろいろな場面で使われるばねですが、理科の問題として解いてみると、直感とは違った力のかかり方をするため、混乱してしまうことがあります。今回は、そんなばねの基本的な考え方を解説します。ばねの問題に苦手意識があり、基礎から復習したい方、ばねのことをこれから学習し始めるという方は、ぜひ最後の問題演習まで挑戦してみてください！それでは早速解説していきましょう。

Contents

1 ばねの基本的な考え方
- 1.1 自然長とは？
- 1.2 ばねの伸び方の基本
2 練習問題
- 2.1 問題
- 2.2 解答
3 おわりに
4 おすすめ記事
5 参考

ばねの基本的な考え方

自然長とは？

ばねには「自然長」という言葉がよく出てきます。日常ではあまり使わない言葉ですが、ばねの問題を解くときには当たり前のように使われます。「自然長」を一言で表すと、「ばねを伸び縮みさせる前の長さ」です。ばねの重要な性質として、伸びたり縮んだりすることがあげられますが、ばねの自然長とは、これらの操作をする前の長さです。「ばねが\(1\,\mathrm{cm}\)伸びた」といえば、ばねの長さは\(1\,\mathrm{cm}\)ではなく、「ばねの自然長から\(1\,\mathrm{cm}\)伸びた長さ」ということになります。つまり、ばねの長さとは

ばねの長さ\(=\)ばねの自然長\(+\)ばねの伸びた長さ

あるいは

ばねの長さ\(=\)ばねの自然長\(–\)ばねが縮んだ長さ

となります。

ばねの伸び方の基本

ばねの伸びた長さは、基本的にばねにかかる力に比例します。これはどういうことかというと、ばねにかかる力が1倍、2倍、3倍…と増えていくと、ばねのの伸び（ばねの長さではない）も1倍、2倍、3倍…と長くなります。この性質は非常に重要です。次の問題で具体的に考え、比例の関係があることを覚えておきましょう。

問題

自然長が\(5\,\mathrm{cm}\)のばねが天井からぶら下がっています。このばねに\(10\,\mathrm{g}\)のおもりをぶら下げると、ばねの長さは\(6\,\mathrm{cm}\)になりました。このばねに\(20\,\mathrm{g}\)のおもりをぶら下げると、ばねの長さは何\(\mathrm{cm}\)になるかを答えよ。

解答
この問題では、自然長が\(5\,\mathrm{cm}\)のばねの長さが、\(10\,\mathrm{g}\)のおもりをつけることで\(6\,\mathrm{cm}\)になる。つまり、おもり\(10\,\mathrm{g}\)あたりのばねの伸びは、
おもり\(10\,\mathrm{g}\)あたりのばねの伸び\(=6\,\mathrm{cm}-5\,\mathrm{cm}=1\,\mathrm{cm}\)となります。これより、おもりが\(20\,\mathrm{g}\)になったときのばねの伸びは、
おもりが\(20\,\mathrm{g}\)のときのばねの伸び\(=(20\,\mathrm{g}\div 10\,\mathrm{g})\times 1\,\mathrm{cm} = 2\,\mathrm{cm}\)となる。したがって、ばねの長さは、
おもりが\(20\,\mathrm{g}\)のときのばねの長さ\(=\)ばねの自然長\(+\)ばねの伸び\(=5\,\mathrm{cm}+2\,\mathrm{cm}=7\,\mathrm{cm}\)と求めることができる。

練習問題

問題

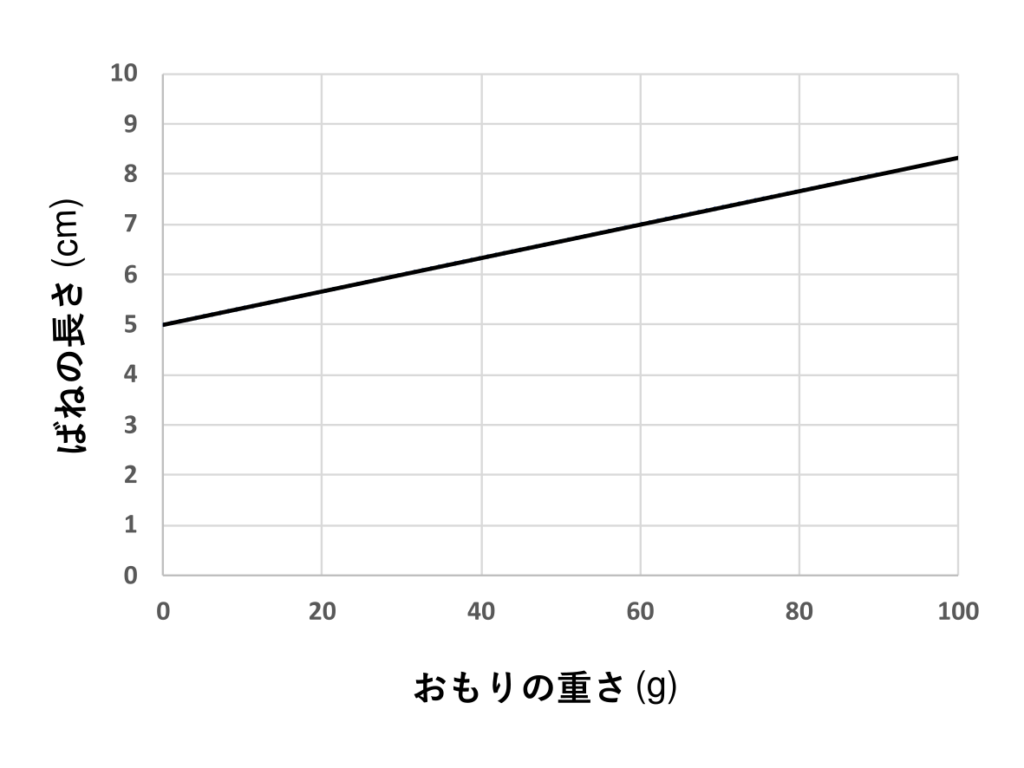
ばねが天井からぶら下がっており、ばねにおもりをぶら下げることを考える。おもりの重さを変化させると、ばねの長さは下の図のように変化する。このとき、ばねの自然長の長さを答えよ。また、ある重さのおもりをぶら下げたときに、ばねの長さが\(6.5\,\mathrm{cm}\)になった。このときのおもりの重さが何\(\mathrm{g}\)であるかを答えよ。

解答

まずばねの自然長は、おもりをつけていないときのばねの長さである。そこで図を見ると、おもりの重さが\(0\,\mathrm{g}\)のときのばねの自然長は\(5\,\mathrm{cm}\)である。したがって、自然長は\(5\,\mathrm{cm}\)である。

次に、おもりの重さを求めるために、ばねの伸び\(1\,\mathrm{cm}\)あたりのおもりの重さが何\(\mathrm{g}\)であるかを求める。そこで図を見ると、おもりの重さが\(60\,\mathrm{g}\)のときのばねの長さは\(7\,\mathrm{cm}\)である。このときのばねの伸びは、（ばねの長さ）-（ばねの自然長）\( = 7\,\mathrm{cm}-5\,\mathrm{cm}\)である。よって、ばねの伸び\(1\,\mathrm{cm}\)あたりのおもりの重さは

\(60\,\mathrm{g}\div (2\,\mathrm{cm}\div 1\,\mathrm{cm}) = 30\,\mathrm{g}\)

となる。また、ばねの長さが\(6.5\,\mathrm{cm}\)のときのばねの伸びは\(6.5\,\mathrm{cm}-5\,\mathrm{cm}=1.5\,\mathrm{cm}\)である。これらより、ばねの伸びが\(1.5\,\mathrm{cm}\)のときのおもりの重さは

\(30\,\mathrm{g}\times (1.5\,\mathrm{cm}\div 1\,\mathrm{cm}) = 45\,\mathrm{cm}\)

と求めることができる。

おわりに

登録6000人以上！
本サイト、中学受験ナビの監修も務めている『開成番長』こと繁田和貴が執筆する完全無料のメールマガジンでは、主に中学受験生のお子さんをお持ちの方へ向けた様々なお役立ち情報を配信中！
さらに今なら登録者にはもれなく「開成番長・繁田の両親が語る繁田の中学受験PDF」をプレゼント！
登録及び登録解除も簡単ですので、お気軽にご登録ください。