皆さんは「てこと力のつり合い」の問題と聞いてどのようなものを思い浮かべますか? 単純なてこの問題を想像する人もいれば、棒とおもりが何個も組み合わさった複雑な問題を思い浮かべる人もいるかもしれませんね。実際には、「てこの力のつり合い」には様々なパターンがあり、ばねや浮力、滑車と組み合わせた複合問題が出題されることも多いです。
「勉強する範囲が多すぎて何から始めたらいいかわからない!」と感じた場合は、とにかく一つ一つの分野に集中して取り組みましょう。「いま自分がどの分野の勉強をしているのか」を意識しながら勉強すれば、複数の分野の知識が積み重なってきても、混乱することがなくなります。
さて、今回は「てこと力のつり合い」と「浮力」の複合問題について解説します。「そんな問題見たことない!」という人もいるかもしれませんが、実際に入試問題でも出題されています。本記事でも「てこと力のつり合い」と「浮力」を使った入試問題の解説をしますので、興味のある人はぜひ解いてみてください! 「てこと力のつり合い」や「浮力」に関する基本的な内容は以下の記事でも解説しています。今回は複合問題なので、これらの知識がまだ身についていないという人は復習がてら参考にしてください。

それでは解説に入ります!
Contents
「てこと力のつり合い」、「浮力」の基礎をおさらいしながら問題を解いてみよう!
では早速、問題を解きながら、「てこと力のつり合い」と「浮力」の複合問題に触れていきましょう。この時点で問題が解ける必要はありません。問題を解説しながら必要になる知識を説明していくので、じっくり理解していけば大丈夫です。
問題
図のように、左端から\(20\,\mathrm{cm}\)の位置をばねばかりでつり下げた長さ\(60\,\mathrm{cm}\)の棒の左側に\(40\,\mathrm{g}\)のおもりを、右側に\(30\,\mathrm{g}\)のおもりをつるし、右側のおもりを完全に水の中に入れました。次の問題に答えなさい。なお、おもりを水中に入れたあとの棒は水平になっており、この棒の重さは無視できる。
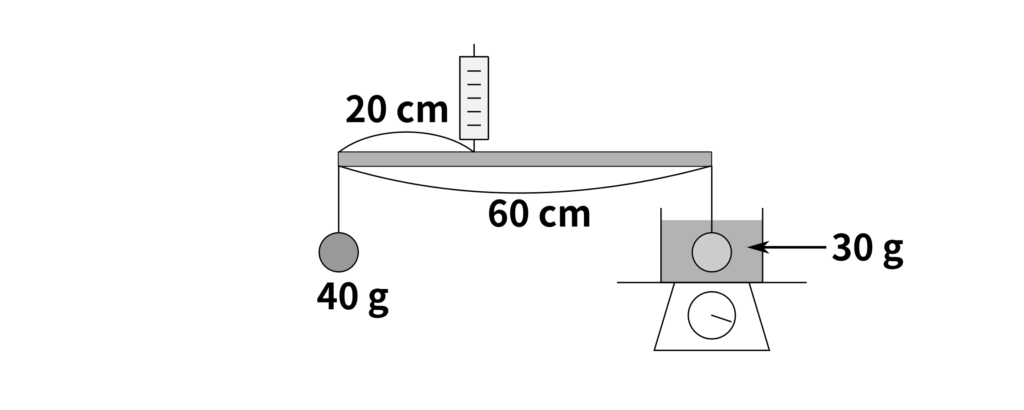
(1) ばねはかりの示す値は何\(\,\mathrm{g}\)ですか。
(2) 水の中におもりを入れる前の台ばかりの示す値は\(300\,\mathrm{g}\)でした。おもりを完全に入れたあとの台ばかりの示す値は何\(\,\mathrm{g}\)ですか。
(3) 水の密度を\(1\,\mathrm{g\,/\,cm^3}\)とすると、右側のおもりの体積は何\(\,\mathrm{cm^3}\)でしょうか。
(4) 右側の\(30\,\mathrm{g}\)のおもりを、同じ重さで体積の小さいものに変えると、台ばかりの示す値はどのように変化しますか。
(5) 右側のおもりを一度水の中から取り出し、代わりに水よりも密度の大きい液体の中に完全に入れると、台ばかりの示す値はどのように変化しますか。
解答に入る前に基本知識をおさらいしておきましょう。詳しくは、先に紹介した過去記事を参考にしてください。
てこと力のつり合い
- 力のつり合いには「上下の力のつり合い」と「モーメントのつり合い」の二つがある
- 上下の力のつり合いとは、(上向きにかかる力)=(下向きにかかる力、または重さ)のことである。
- モーメントの大きさは、「支点」の位置を決めた上で、(モーメントの大きさ)=(支点からの距離)×(重さ、または力)で求める
- モーメントのつり合いとは、(支点を中心に時計回りに回転する方向のモーメントの大きさ)=(支点を中心に反時計回りに回転する方向のモーメントの大きさ)のことである。
浮力
- 台ばかりで重さがわかるとき、浮力は(浮力)=(ものの重さ)-(液体に入れたものの重さ)となる
- ものが沈んでいる部分の体積がわかるとき、浮力は(浮力)=(液体の密度)×(ものが沈んでいる部分の体積)となる
- つるされたものの重さをはかるとき(台ばかりにかかる重さ)=(ビーカーと液体の重さ)+(ものの重さ)-(ものをつるす力)となる。
- ばねばかりでものの重さをはかるとき(ばねばかりにかかる重さ)=(ものの重さ)-(浮力)となる。
解答
(1) この問題はまず、「モーメントのつり合い」で右端の糸にかかる力を求めたのち、「上下の力のつり合い」でばねばかりにかかる力を計算する問題です。
ばねばかりの位置を支点にとると、左のおもりによるモーメントの大きさは
\(40\,\mathrm{g} \times 20\,\mathrm{cm}\)
となります。次に、右端の糸にかかる力を\(\text{□}\,\mathrm{g}\)として、右端の糸によるモーメントの大きさを計算すると
\(\text{□}\,\mathrm{g} \times \mathrm{cm}\)
となります。最後に、「モーメントのつり合い」を考えると、
\(40\,\mathrm{g} \times 20\,\mathrm{cm} = \text{□}\,\mathrm{g} \times \mathrm{cm}\)
となります。よって、右端の糸にかかる力は
\(20\,\mathrm{g}\)
となります。次に、「上下の力のつり合い」を考えます。下向きにかかる力は
(左のおもりの重さ)+(右端の糸にかかる力)=\(40\,\mathrm{g} + 20\,\mathrm{g}\)
となります。上向きにかかる力は
(ばねばかりにかかる力)=\(\text{□}\,\mathrm{g}\)
となります。「上下の力のつり合い」を考えると、
\(\text{□}\,\mathrm{g} = 40\,\mathrm{g} + 20\,\mathrm{g}\)
となります。したがって、ばねばかりが示す値は
\(60\,\mathrm{g}\)
と求めることができます。
(2) この問題は、(台ばかりにかかる重さ)=(ビーカーと液体の重さ)+(ものの重さ)ー(ものをつるす力)の関係を使います。
問題文より、ビーカーと液体を合わせた重さは\(300\,\mathrm{g}\)とわかります。また、おもりの重さは\(30\,\mathrm{g}\)です。おもりを完全に入れたあと、(1)より、おもりは右端の糸によって\(20\,\mathrm{g}\)の力でつるされているので、台ばかりにかかる重さを\(\text{□}\,\mathrm{g}\)とすると、
\(\text{□}\,\mathrm{g} = 300\,\mathrm{g} + 30\,\mathrm{g} – 20\,\mathrm{g}\)
となります。したがって、台ばかりにかかる重さは
\(310\,\mathrm{g}\)
と求めることができます。
(3) この問題は、(浮力)=(ものの重さ)ー(液体に入れたものの重さ)と、(浮力)=(液体の密度)×(ものが沈んでいる部分の体積)の関係を使います。
まず、浮力の大きさを求めましょう。おもりの重さは\(30\,\mathrm{g}\)、水に入れたおもりの重さは、右側の糸がおもりをつるす力と同じなので、\(20\,\mathrm{g}\)です。このことは、糸とおもりの上下の力のつり合いを考えれば理解できると思います。したがって、浮力の大きさは
(浮力)=(ものの重さ)ー(液体に入れたものの重さ)=\(30\,\mathrm{g} – 20\,\mathrm{g} = 10\,\mathrm{g}\)
となります。
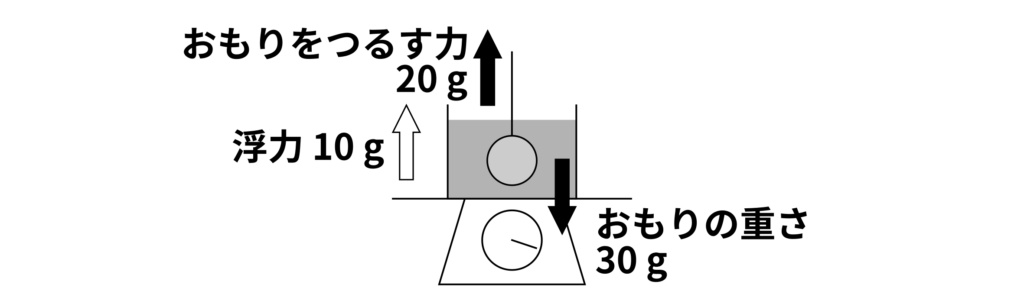
次に、おもりの体積を求めましょう。ここでは、おもりは水の中に完全に沈んでいるので、「ものが沈んでいる部分の体積」は、「おもりの体積」となります。液体の密度は\(1\,\mathrm{g\,/\,cm^3}\)(つまり、水\(1\,\mathrm{g}\)が\(1\,\mathrm{cm^3}\)ということ)なので、ものが沈んでいる部分の体積、つまりおもりの体積を\(\text{□}\,\mathrm{cm^3}\)とすると
\(10\,\mathrm{g} = 1\,\mathrm{g\,/\,cm^3} \times \text{□}\,\mathrm{cm^3}\)
となります。したがって、おもりの体積は
\(10\,\mathrm{cm^3}\)
と求めることができます。
(4) この問題は、(浮力)=(液体の密度)×(ものが沈んでいる部分の体積)と、(台ばかりにかかる重さ)=(ビーカーと液体の重さ)+(ものの重さ)ー(ものをつるす力)の関係を使います。
まず、おもりを同じ重さで体積の小さいものにかえるということは、「ものが沈んでいる部分の体積」が小さくなるということになります。(浮力)=(液体の密度)×(ものが沈んでいる部分の体積)の関係を使うと、浮力は小さくなるということがわかります。
浮力が小さくなるということは、「ものをつるす力」が大きくなることを意味します。これは先ほどの問題でも触れた、上下の力のつり合いを考えればわかりますね。浮力はものを持ち上げる力なので、その力が小さくなると、より大きな力でものをつるす必要があるのです。
(台ばかりにかかる重さ)=(ビーカーと液体の重さ)+(ものの重さ)ー(ものをつるす力)の関係を使うと、「ものをつるす力」が大きくなったので、「台ばかりにかかる重さ」は小さくなることがわかります(「ものをつるす力」は引き算であることに注意!)。したがって、
「台ばかりにかかる重さは小さくなる」
が答えになります。
(5) この問題は、(浮力)=(液体の密度)×(ものが沈んでいる部分の体積)と、(台ばかりにかかる重さ)=(ビーカーと液体の重さ)+(ものの重さ)ー(ものをつるす力)の関係を使います。
水を、より密度の大きい液体(例えば塩水)にかえると、(浮力)=(液体の密度)×(ものが沈んでいる部分の体積)の関係から、浮力が大きくなります。これは、海水浴を思い浮かべればわかりやすいと思います。海は塩水で、真水よりも密度が大きいです。学校のプールで泳ぐときよりも海で泳ぐときの方が体が浮く感じがするのは、浮力が大きくなっているからです。ちなみに、この塩水の濃度がもっと高くなると、浮き輪がなくても体が浮いた状態になります(気になる人は、「死海」で調べてみてください)。
あとは、先ほどの問題の逆です。上下の力のつり合いから、「ものをつるす力」が小さくなり、(台ばかりにかかる重さ)=(ビーカーと液体の重さ)+(ものの重さ)ー(ものをつるす力)の関係を使うと、「台ばかりにかかる重さ」は大きくなります。したがって、
「台ばかりにかかる重さは大きくなる」
が答えになります。
さて、「てこと力のつり合い」と「浮力」を使った一通りの解説は終わりです。「一度で理解できなかった……」という人も、あきらめずに何度か問題に取り組んでみてください!
「てこと力のつり合い」、「浮力」を使った入試問題に挑戦しよう!
ここからは、入試問題の解説に入ります。とはいっても、ものすごく難易度があがるわけではないので、落ち着いて取り組んでみましょう!
明治大学付属明治中学校 2018年 改題
問題
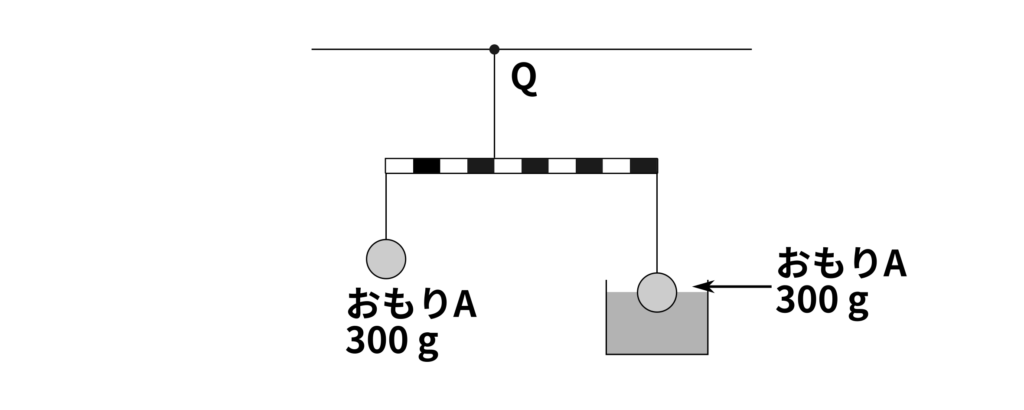
おもり、等間隔に目盛りのついた板、糸、水の入った水槽を使って図のように組み合わせ、天井から糸でつるしたところ、板は水平になりました。おもりAの重さは\(300\,\mathrm{g}\)です。これについて、問いに答えなさい。ただし、目盛りのついた板、糸の重さは無視できるものとします。また、水\(1\,\mathrm{cm^3}\)の重さは\(1\,\mathrm{g}\)とします。
下図の右側のおもりAは、一部が水中に沈んでいます。おもりAの水中に沈んでいる部分の体積は何\(\,\mathrm{cm^3}\)ですか。また、天井Qにかかる力は何\(\,\mathrm{g}\)ですか。
解答
まずは、「モーメントのつり合い」を用いて右端の糸にかかる力を計算しましょう。
板を支えている糸の場所を支点とすると、左側のおもりAは支点から数えて4つ目の目盛りの場所にあります。したがって、左側のおもりSによる力のモーメントは
\(300\,\mathrm{g} \times 4\)
となります。これが、「支点を中心に反時計回りに回転するモーメント」です。次に、右側の糸にかかる力を\(\text{□}\,\mathrm{g}\)として、モーメントを計算すると、右側の糸は支点から数えて6つ目の目盛りの場所にあるので、
\(\text{□}\,\mathrm{g} \times 6\)
となります。最後に、「モーメントのつり合い」を考えると、
\(300\,\mathrm{g} \times 4 = \text{□}\,\mathrm{g} \times 6\)
となります。これより、右側の糸にかかる力は
\(200\,\mathrm{g}\)
となります。次に、右側のおもりAにかかる浮力を計算します。おもりA自体の重さは\(300\,\mathrm{g}\)であるのに対し、それを支える糸にかかる力が\(200\,\mathrm{g}\)なので、
\(300\,\mathrm{g} – 200\,\mathrm{g} = 100\,\mathrm{g}\)
の浮力がおもりAにかかっています。浮力は
(浮力)=(液体の密度)×(ものが沈んでいる部分の体積)
で計算でき、水\(1\,\mathrm{cm^3}\)の重さは\(1\,\mathrm{g}\)と与えられているので、密度は\(1\,\mathrm{g\,/\,cm^3}\)です。よって、沈んでいる部分の体積は
\(100\,\mathrm{cm^3}\)
と求めることができます。最後に、天井Qにかかる力を計算しましょう。これは、「上下の力のつり合い」を考えればよく、天井Qにかかる力を\(\text{□}\,\mathrm{g}\)とすると、
\(\text{□}\,\mathrm{g} = 300\,\mathrm{g} + 200\,\mathrm{g}\)
となるので、
\(500\,\mathrm{g}\)
と求めることができます。
東邦大学付属東邦中学校 2018年
問題
次の文章を読み、あとの(1)~(3)の問いに答えなさい。ただし、ばねや糸の重さは考えないものとします。
もとの長さが\(20\,\mathrm{cm}\)で、重さ\(100\,\mathrm{g}\)のおもりをつるすと、\(1.2\,\mathrm{cm}\)のびるばねSがあります。図1のように、太さが一様でない長さ\(50\,\mathrm{cm}\)の棒Xの点PにこのばねSをつけてつるすと、棒Xはつり合い、ばねSの長さは\(35\,\mathrm{cm}\)になりました。
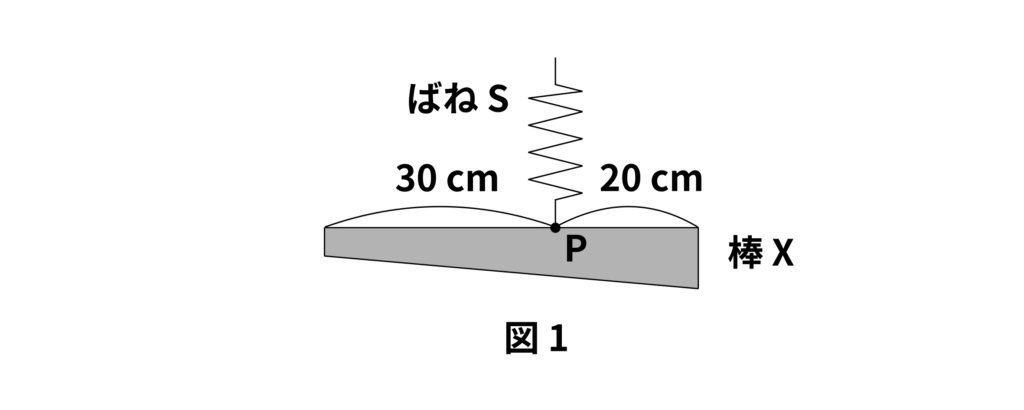
(1) 棒Xの重さは何\(\,\mathrm{g}\)ですか。
物体を液体の中に入れたとき、液体がその物体を浮き上がらせようとする力を浮力といいます。浮力の大きさは、物体がおしのけた液体の重さと同じになります。
(2) ビーカーの中に\(100\,\mathrm{cm^3}\)あたり重さが\(120\,\mathrm{g}\)の食塩水が入っています。図2のように、ばねSを棒Xの中心に取り付け、棒Xの太い方の端に重さ\(200\,\mathrm{g}\)のおもりAを、棒Xの細い方の端に重さ\(600\,\mathrm{g}\)のおもりBを、それぞれ糸でつるし、おもりBをビーカーに入った食塩水の中に完全にしずめたところ、棒Xはつり合いました。このとき、ばねSの長さは何\(\,\mathrm{cm}\)ですか。小数第1位まで答えなさい。
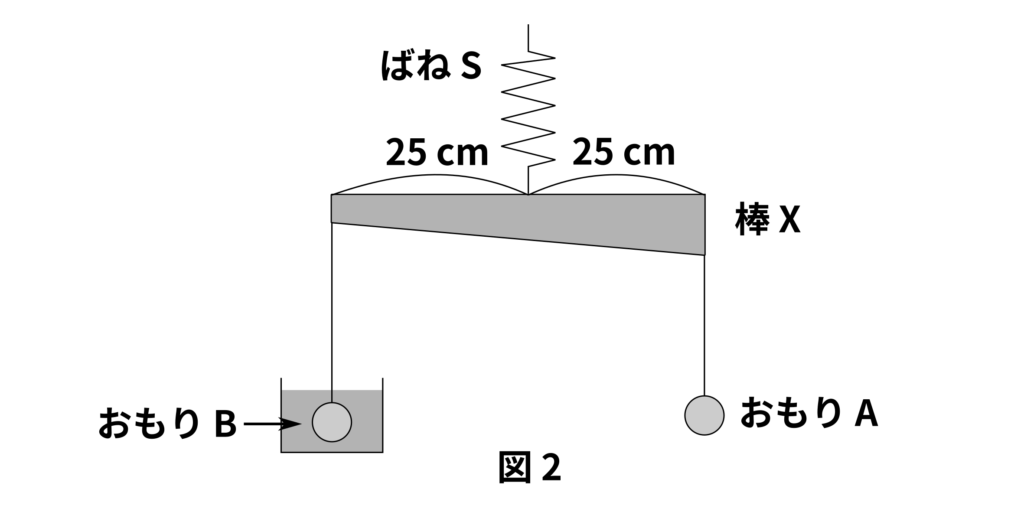
(3) (2)のおもりBの体積は何\(\,\mathrm{cm^3}\)ですか。
解答
(1) この問題は、ばねSの長さから、棒Xの重さを考えます。
問題文より、棒XをつるしたときのばねSののびは
\(35\,\mathrm{cm} – 20\,\mathrm{cm} = 15\,\mathrm{cm}\)
となります。このばねSはおもり\(100\,\mathrm{g}\)あたり\(1.2\,\mathrm{cm}\)のびるので、棒Xの重さは
\(15\,\mathrm{cm} \div 1.2\,\mathrm{cm} \times 100\,\mathrm{g} = 1250\,\mathrm{g}\)
と求めることができます。
(2) この問題は、「モーメントのつり合い」からおもりBをつるす糸にかかる力を求めたあと、「上下の力のつり合い」からばねSにかかる力を求め、ばねSののびを計算します。
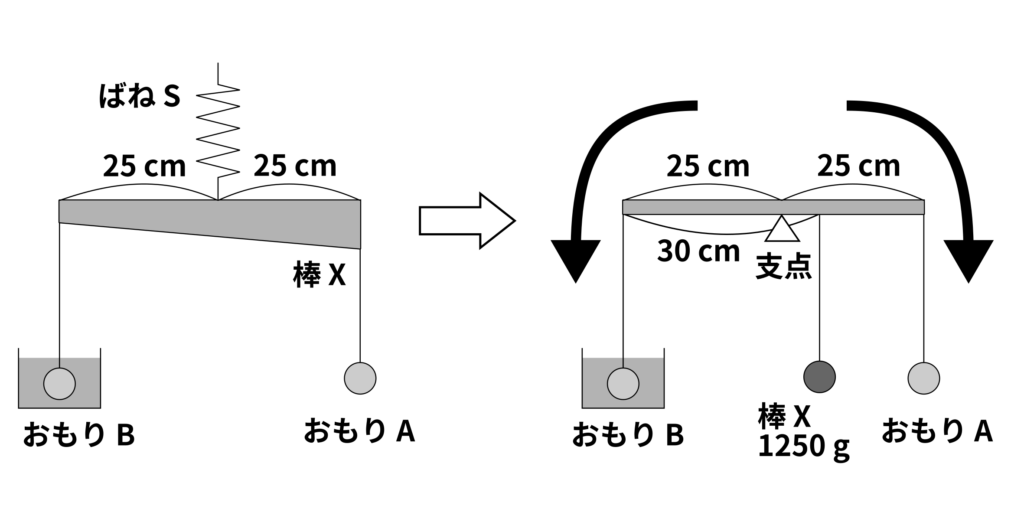
まず、支点をばねSの位置におき、おもりAによるモーメントの大きさを考えると、
\(200\,\mathrm{g} \times 20\,\mathrm{cm}\)
となります。これは、支点を中心に時計回りに回転する方向のモーメントです。次に、棒Xによるモーメントの大きさを考えます。
(1)で棒Xはつり合っているので、棒Xの重心の位置は左端から\(30\,\mathrm{cm}\)の位置とわかります。支点となるばねSの位置は左端から\(25\,\mathrm{cm}\)の位置にあるので、支点と棒Xの距離は\(5\,\mathrm{cm}\)となります。(1)から、棒Xはこの位置に\(1250\,\mathrm{g}\)の重さがかかると考えられるので、棒Xによるモーメントの大きさは
\(1250\,\mathrm{g} \times 5\,\mathrm{cm}\)
となります。これも、支点を中心に時計回りに回転する方向のモーメントです。また、おもりBをつるす糸にかかる力を\(\text{□}\,\mathrm{g}\)とすると、おもりBをつるす糸によるモーメントの大きさは
\(\text{□}\,\mathrm{g} \times 25\,\mathrm{cm}\)
となります。これは、支点を中心に反時計回りに回転する方向のモーメントです。最後に、「モーメントのつり合い」を考えると
\(200\,\mathrm{g} \times 20\,\mathrm{cm} + 1250\,\mathrm{g} \times 5\,\mathrm{cm} = \text{□}\,\mathrm{g} \times 25\,\mathrm{cm}\)
となります。したがって、おもりBをつるす糸にかかる力は
\(450\,\mathrm{g}\)
となります。次に、「上下の力のつり合い」を考えると、ばねSにかかる力は
\(200\,\mathrm{g} + 1250\,\mathrm{g} + 450\,\mathrm{g} = 1900\,\mathrm{g}\)
となります。よって、ばねSののびは
\(1900\,\mathrm{g} \div 100\,\mathrm{g} \times 1.2\,\mathrm{cm} = 22.8\,\mathrm{cm}\)
となり、これにもとのばねSの長さ\(20\,\mathrm{cm}\)を足すと、ばねSの長さは
\(20\,\mathrm{cm} + 22.8\,\mathrm{cm} = 42.8\,\mathrm{cm}\)
と求めることができます。
(3) この問題は、(浮力)=(ものの重さ)ー(液体に入れたものの重さ)と、(浮力)=(液体の密度)×(ものが沈んでいる部分の体積)の関係を使います。
まず、おもりBにかかる浮力の大きさを求めましょう。おもりBの重さは\(600\,\mathrm{g}\)、おもりBをつるす糸にかかる力、すなわち、液体の中にあるおもりBの重さは(1)より、\(450\,\mathrm{g}\)です。(浮力)=(ものの重さ)ー(液体に入れたものの重さ)の関係を使うと、浮力の大きさは
\(600\,\mathrm{g} – 450\,\mathrm{g} = 150\,\mathrm{g}\)
となります。次に、おもりBの体積を求めます。問題文より、液体の密度は\(120\,\mathrm{g} \div 100\,\mathrm{cm^3}\)です。いま、おもりBは完全に液体に沈んでいるので、「ものが沈んでいる部分の体積」は「おもりBの体積」となります。(浮力)=(液体の密度)×(ものが沈んでいる部分の体積)の関係を使うと、おもりBの体積は
\(150\,\mathrm{g} \div 120\,\mathrm{g} \times 100\,\mathrm{cm^3} = 125\,\mathrm{cm^3}\)
と求めることができます。
最後に
本記事では、「てこと力のつり合い」と「浮力」を組み合わせた問題について解説しました。複合問題とは言えども、特別な知識が必要なわけではなく、「てこと力のつり合い」と「浮力」のそれぞれを丁寧に考えれば、答えに近づくということが理解できたでしょうか? 最後の入試問題がすべて正解できなくても、本記事で紹介した最初の問題や、それぞれの基礎を解説した記事を参考にすることで解けるようになると思うので、これからも勉強を頑張ってください!
おすすめ記事
- てこのつり合いのまとめ その1
- てこのつり合いのまとめ その2
- 【中学受験理科】てこと力のつり合い ~太さが一様でない棒を使った問題をマスターしよう!~
- 浮力が苦手な人必見!点数をとる方法は?
- 物理の勉強法~苦手な人への処方箋
- 【中学受験】今だからできる!理科勉強法・克服法 物理編

















