Contents
問題① 簡単な対応関係から掴んでいこう!
まずは基本的な問題から進めていきましょう。応用編の記事とはいきなり難問に挑むのはハードルが高いでしょう,そのためウォームアップがてらミスの無いように進めていきましょう。
次の□にあてはまる数を求めなさい。
下の図は,長方形状のテープを折り目ABで折り返した図です。このとき,角ウの大きさは□度です。
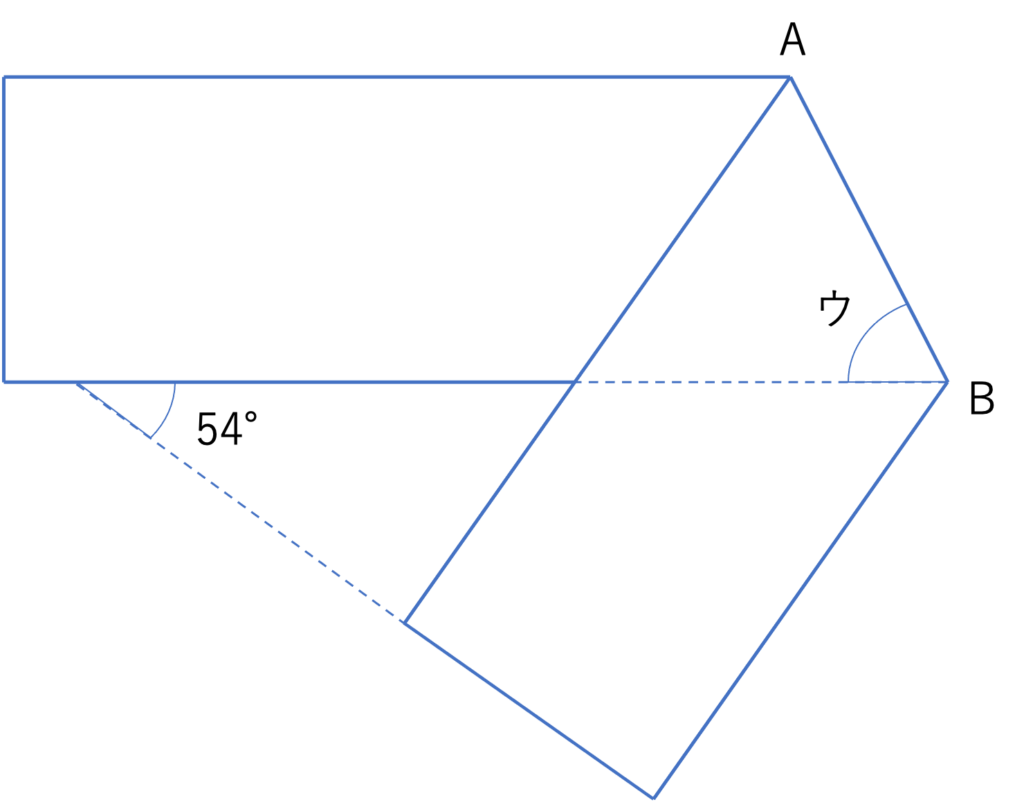
(佼成学園女子中学校(2014),一部改題)
解説①
それではここからは1問目の解説に移りましょう。今回の問題では長方形が登場し,その右側の部分が左下に向かって折られています。この操作だったり問題文だったりから,もう折り返し問題であるということは明確ですね。
この範囲の問題では起こりづらいですが,他の文章題や図形の問題では,ときおり何算なのかに関する間違った理解をしてしまうせいで大きく時間をとられてしまうというアクシデントが発生してしまいます。このような事故を防ぐためにも,いま自分が向き合っているのはどの範囲からの出題なのか,は常に意識しておくといいでしょう。
さて一度寄り道したところで本題の解説に移りましょう。先の基礎編振り返りで,この範囲を解くコツは一致・対応する部分への注目ということを取り上げました。
このときに頼りになるのが折れ線への注目です。折る前と折った後の図形は同じになるということを先ほど説明しました。
当たり前ですが,このとき対応する図形は折れ線を軸として鏡合わせになっているのです。今回の図形では折る前の部分が省略されていますが,その部分を新しく書き込み,その上で一致している部分を記すと次のようにまとめられます。
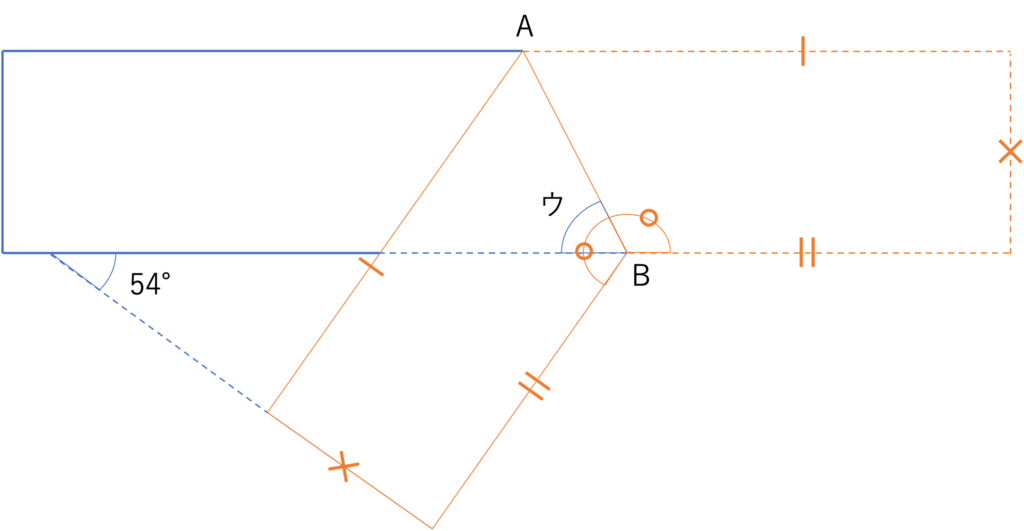
さてここまで関係をまとめられたところで,次は情報を埋めていきましょう。
今回は54°という大きさの角度しか与えられていないですが,三角形の内角の関係などを使えばより多くの数値を導けそうですね。
例えば○で示した角度からウを引いた部分の角度などがその1つとして当てはまります,この部分は長方形の下に出来上がった三角形の内角の関係を使うと大きさが分かりそうです。
全体の内角である180°のうち1つの角度が54°,そしてもう1つの角度が直角つまり90°であるので,この部分は180°-(54°+90°)=180°-144°=36°となります。
この部分は折り返しているという要素,または直接的な答えとは関係ないようにも思えますが,重要なのは情報を整理していくことです。急がば回れではないですが,大体の問題は1つずつ値を求めていくことでしか答えは導けないように作られています。そのためこのように焦らず大きさを考えていきましょう。
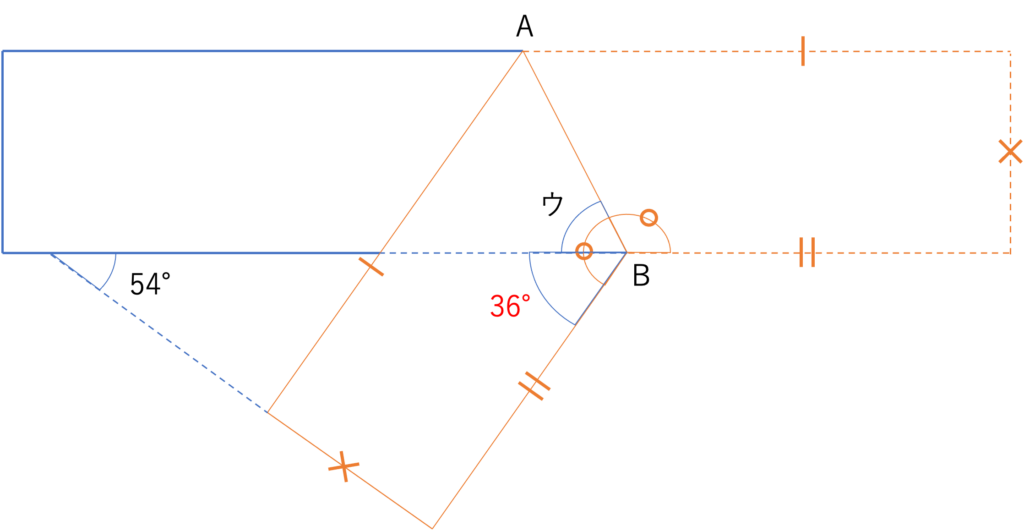
この図から,「ウ」の部分の角度は○の部分の角度から36°を引くことで計算できると判断できますね。ではあとは○の部分を求めれば答えまで導くことができそうです。
ここで折り返しが起こっている線分を対象にした2つの○の角度に注目しましょう。この2つの○の角度が合わさると,直線半周分の180°+先ほど求めた36°になることが分かりますね。したがって○1つ分の角度の大きさは(180°+36°)÷2=216°÷2=108°だと計算できます。
以上のように,折り返した部分を合わせるとこれくらいになるというタイプの情報が図の中に存在することも多いですので,パターンの1つとして覚えておきましょう。さてここまでの情報が分かりましたので,求めた情報から「ウ」の値を計算すると,108°-36°=72°となります。
A.72°
以上のように,受験問題であっても対応関係について理解してしまえば難なく答えを導くことができます。そのためのテクニックとして折れ線への注目だったり,鏡合わせになっていることの確認だったりを忘れないようにしましょう。
問題② いろいろな箇所を行き来しながら考えよう!
続いての問題も対応関係を使う折り返しの問題ですが,この問題では折り返しによって生まれた対応関係と,それ以外のところで生まれた要素とを上手く切り替えながら考えていく必要があります。とはいっても要領は先ほどの問題と同じですので,焦らず解いてみましょう。
下の図のように長方形の紙を対角線で折り返します。このとき,あの角度は何度ですか。
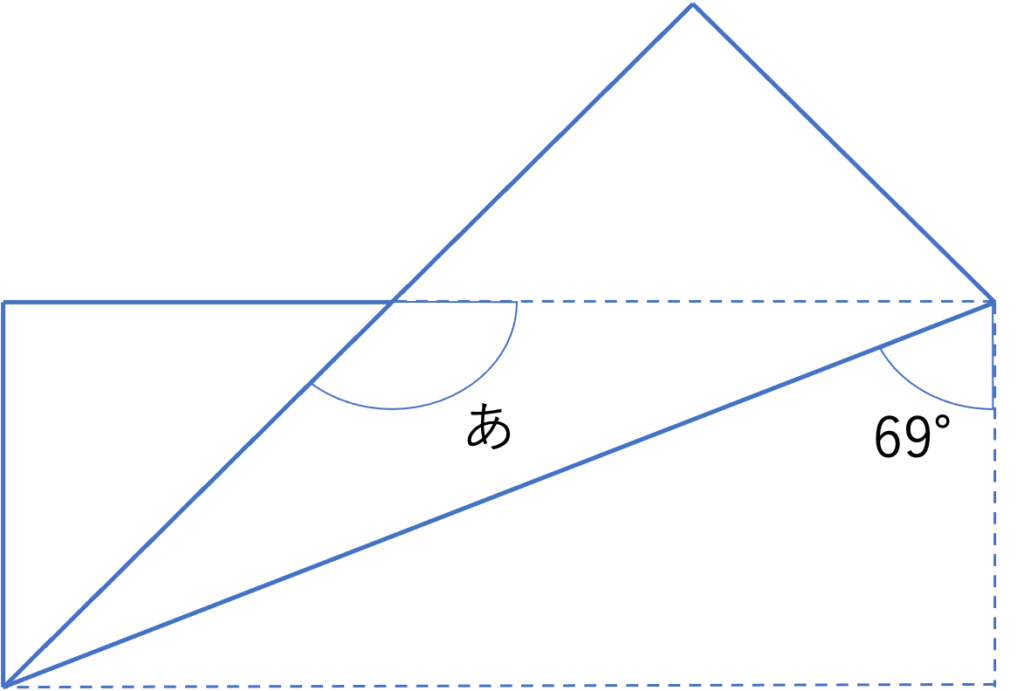
(八雲学園中学校(2016),一部改題)
解説②
では第2問目の解説を行っていきます。この問題でもまずは文章や図表の確認・整理から始めていきましょう。この問題も文中に「折り返し」という言葉が入っている通り,図形の折り返しという範囲からの出題だということが判断できます。
今回は1問目と同じ長方形ではあるものの,右下から左上に向かって折り返しが行われていて,対角線を基準として折り返されています。そしてこの対角線を基準としているということから,次のような対応関係を見出すことができます。
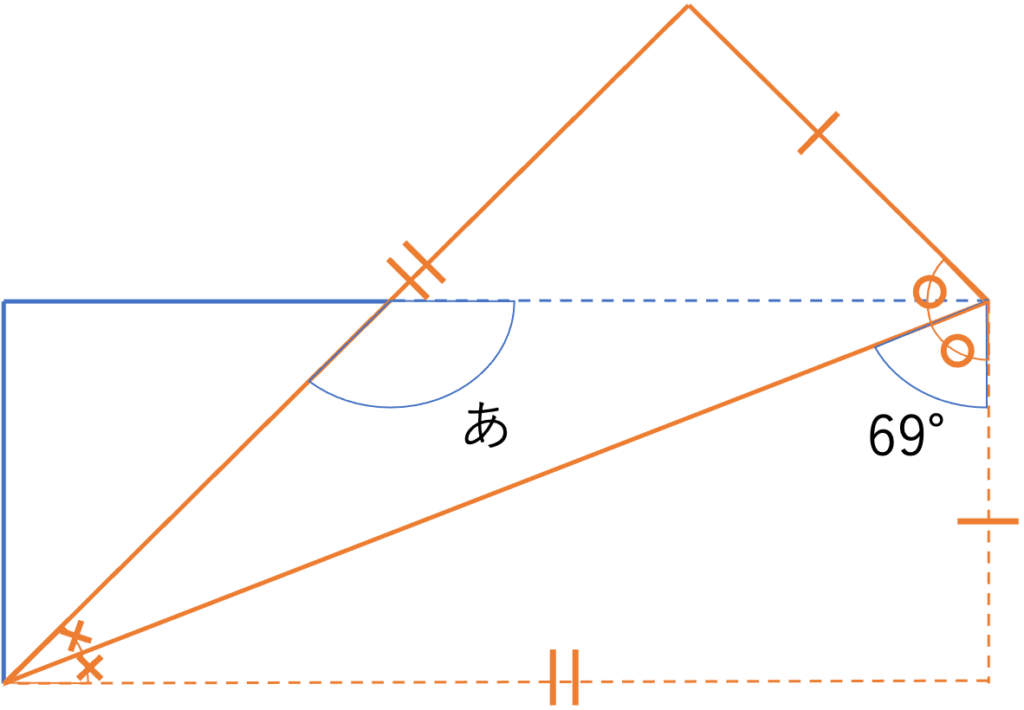
ここまで確認したところで,先ほどの問題を進めていった手順に則って今回も1つずつ情報を埋めていきましょう。
この問題で与えられているのは69°という角度,ならびに長方形の直角という要素だけですので,それらを基にして考えていきます。まず求められそうなのは対角線によって作られた直角三角形の部分ですね。
三角形の内角の和は180°なので,上の図でいう×の部分の角度の大きさは180°-(69°+90°)=180°-159°=21°だと計算できます。
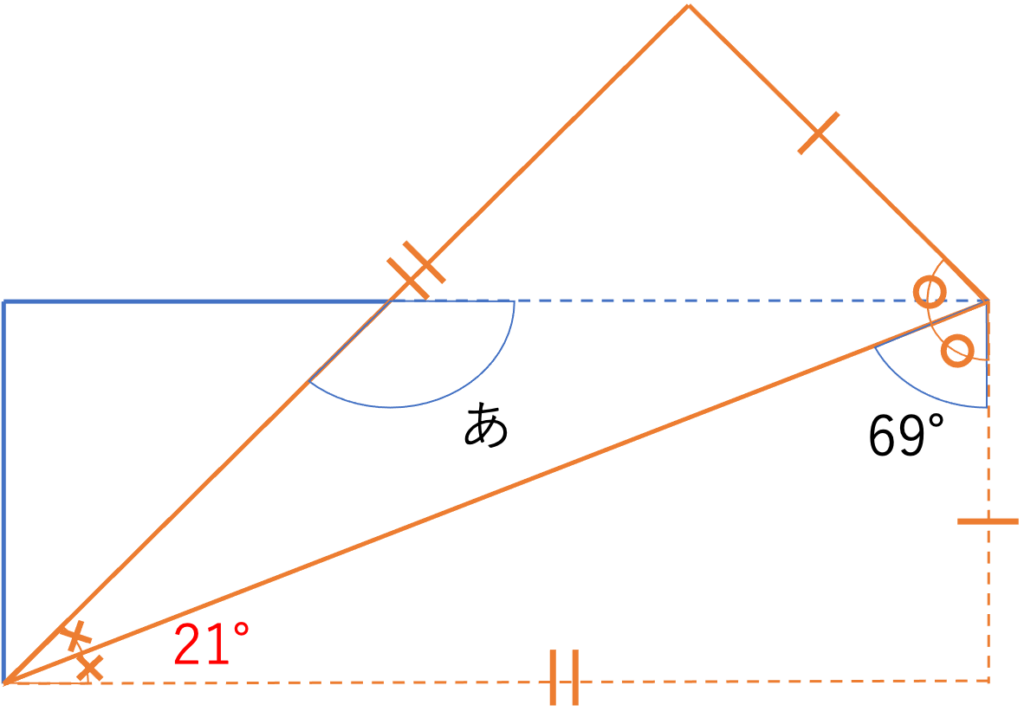
ここで×の部分が21°だということが分かったので,折り返した部分の×の角度の大きさも21°だと分かります。以上のように折り返しによる対応関係と理解していると,情報を次々と埋めることができます。
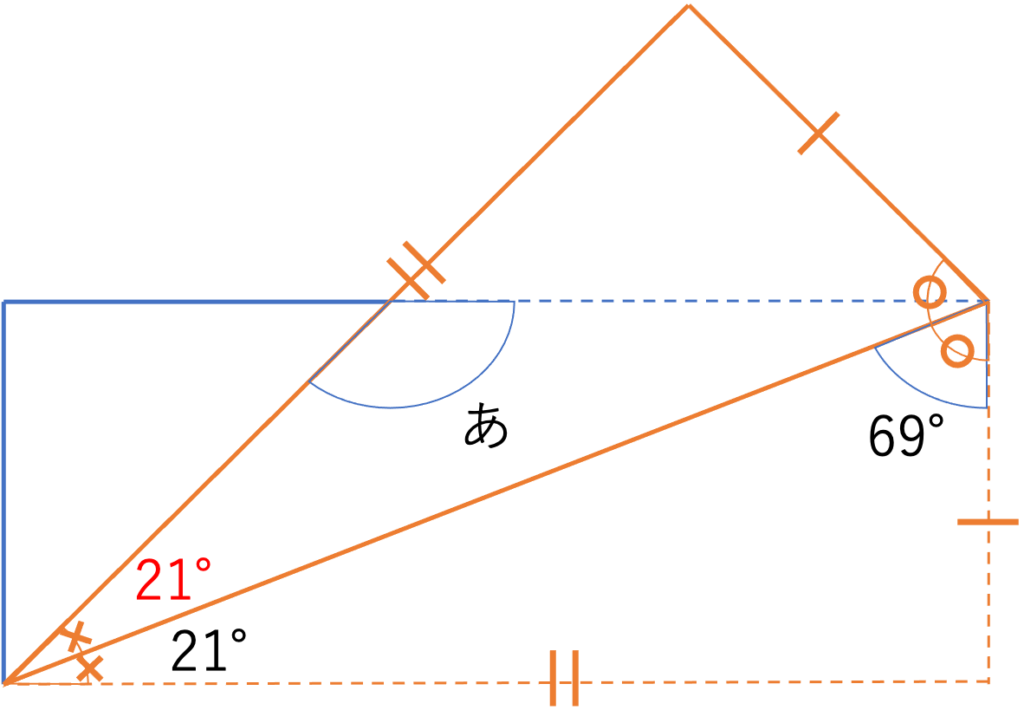
さてここで今回求めるべき答えに立ち返ってみましょう。ここで求めるべきなのは「あ」の大きさです。
この部分は折り返しによって作られた平べったい三角形の1つの角度であるということは,上の図を見ていただけると分かるかと思います。いまこの三角形における角度の1つが「あ」,1つが21°だと求められているので,残りの右上の1つの大きさが計算できれば引き算によって「あ」の値も計算できそうです。
したがって以上の部分に注目すると,この角度は直角から69°を引くことで作られているということが分かります。したがって大きさとしては,90°-69°=21°だと計算できます。
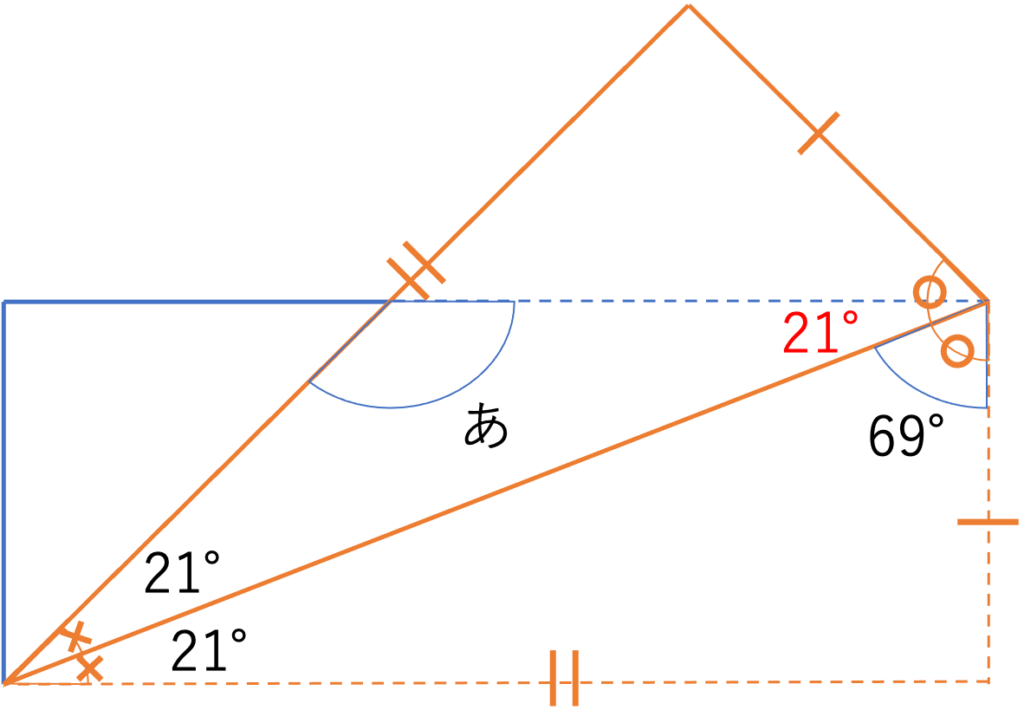
以上のことから,この平べったい図形は21°が共通する二等辺三角形であると判断できますね。
この特徴は答えの計算と直接関わるところではないですが,対応関係であるところとそうでないところ,具体的には左下・右上という視点の行き来が上手くいけばこのような特徴まで見出すことができます。
対角線で折ると二等辺三角形ができる,という性質として頭に入れておくと他の問題を解くのが楽になるかもしれません。さてこれらのことから「あ」の値を計算すると,180°-(21°+21°)=180°-42°=138°だと分かります。
A.138°
問題③ 最短で計算できる手順を考えながら進めてみよう!
それでは最後の問題に移ります。この問題も形としては非常にシンプルですが,何通りかの違った答えの導き方が考えられるので,そのうち最も早く求められそうなルートを考えつつ,間違いのないよう計算する訓練として進めていただけると幸いです。
下の図のように,正三角形ABCの紙をPQを折り目として折りました。そのとき頂点Aが辺BC上の点Dと重なりました。xの角の大きさは何度ですか。
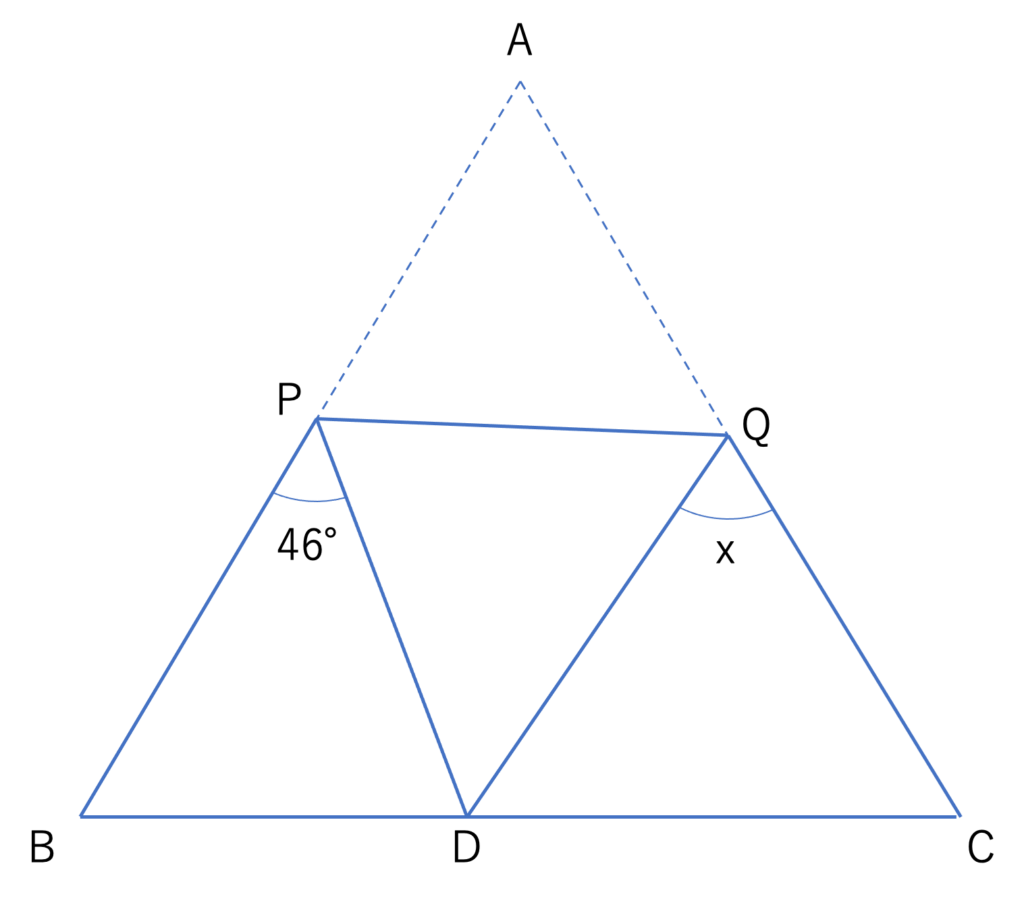
(京華中学校(2019),一部改題)
解説③
ここからは第3問目の解説に移ります。この問題も文章と図形とから折り返しに関する範囲からの出題だ,という判断ができますね。
例によって対応関係を見ていくと,今回の図形はPQという折れ線に沿って図形が鏡合わせになっていることがわかるので,下の図のように内容を整理することができます。
そして今回の図形は正三角形だということも提示されていますので,角A・B・Cがそれぞれ60°であることも併せて書き込んでおきましょう。
そして角Aを折り返して出来た○の部分の角度も同じく60°だと分かるので,その部分にも情報を落とし込むと,以下のようにまとめることができます。
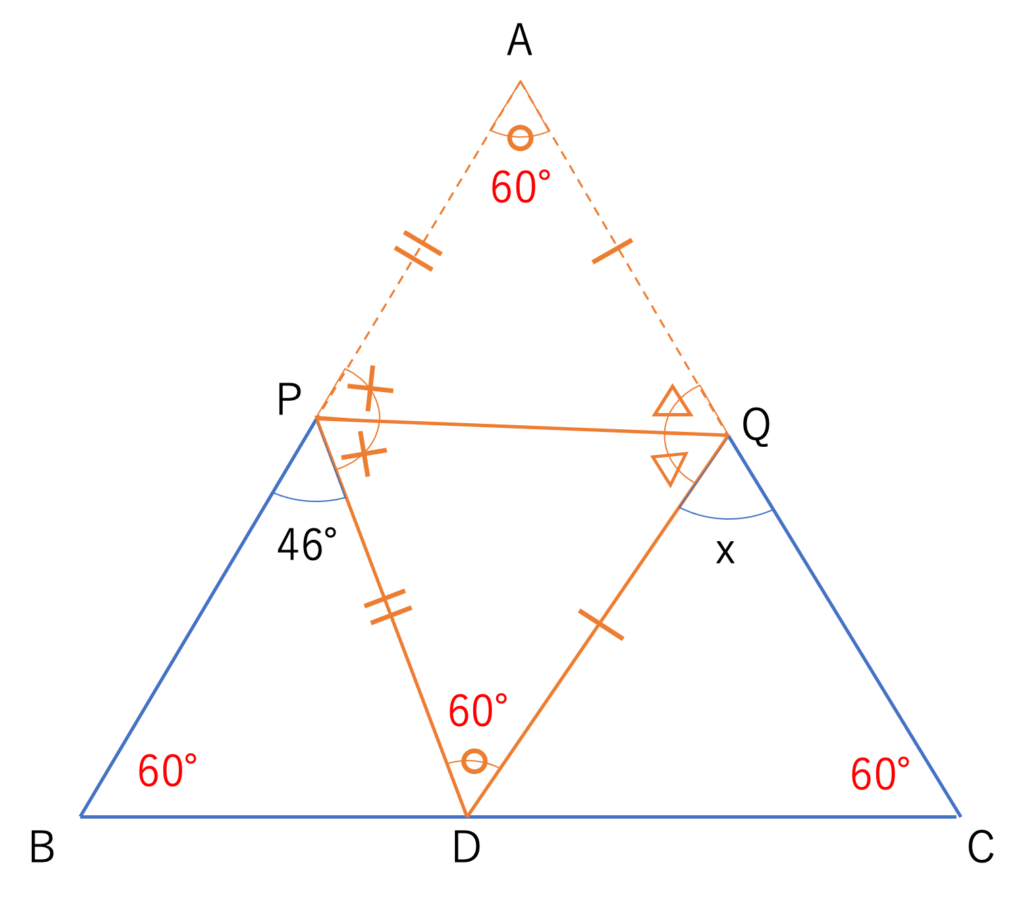
さて以上のところまでまとめられたところでxの大きさについて考えていくのですが,この問題には大きく分けて2つの解答パターンが存在します。
それが点Dの周辺に注目する解き方と,折り返して出来た三角形の角度○・×・△に注目する解き方です。
どちらの方法でも解答の速さはそこまで変わらないのですが,2つの解き方を行き来してしまうと計算の過程に無駄が生じてしまいます。
もちろん順番に情報を埋めてミスなく答えを導いていくことも重要なのですが,それと同じくらい本番ではスムーズに解くことも大切になってきます。
応用編の記事だからこそ,そういった本番を見据えた解き方も意識してみてください。したがって以下ではそれぞれのパターンに応じた解き方をご紹介していきます。
解き方① 点Dに注目する解き方
まずはパターンの1つ目の点Dへの注目から進めていきましょう。
この頂点Dの周囲には3つの角が存在し,そのうち1つは頂点Aを折り返してきた60°だと判明しています。そして3つのうち左側の1つは,三角形PQDの内角の和の関係から大きさを計算できそうですね。180°-(46°+60°)=180°-106°=74°だと計算できます。
そしてこのことから連鎖的に右側の角度についても値が求められそうです。点Dのある直線上の3つの角度を足すと180°になることから,この部分の大きさは180°-(74°+60°)=180°-134°=46°だと分かります。これらのことを一度下の図のようにまとめてみましょう。

そしてここで今回求めるべきである角度xに注目すると,この部分は三角形QDCを構成する角度の1つであることが図から明らかになっています。いまこの三角形のうち1つの角度が60°,もう1つの角度が46°であると計算しましたので,内角の和の関係から答えは180°-(46°+60°)=180°-106°=74°となります。
A.74°
このように点Dの周りにある角度に注目しながら解くのが1つ目のルートです。この過程では×や△の大きさは必要としなかったので,残念ながら計算してしまうと時間の無駄になってしまいます。
このようにロスを避けて計算するということが中学受験では極めて大切になってきますので,考え方の1つとして頭に入れておきましょう。
解き方② 三角形の内角に注目する解き方
それでは続いでは別解となる,×や△への注目についても説明していきましょう。初めに注目するのは×の部分です。この角度はPQによって折り返されているわけですが,2つの×の部分と46°を足したら180°になることが,上の図における点Pの存在する線分に注目すると分かります。このことから×の大きさは,(180°-46°)÷2=67°であると求められますね。
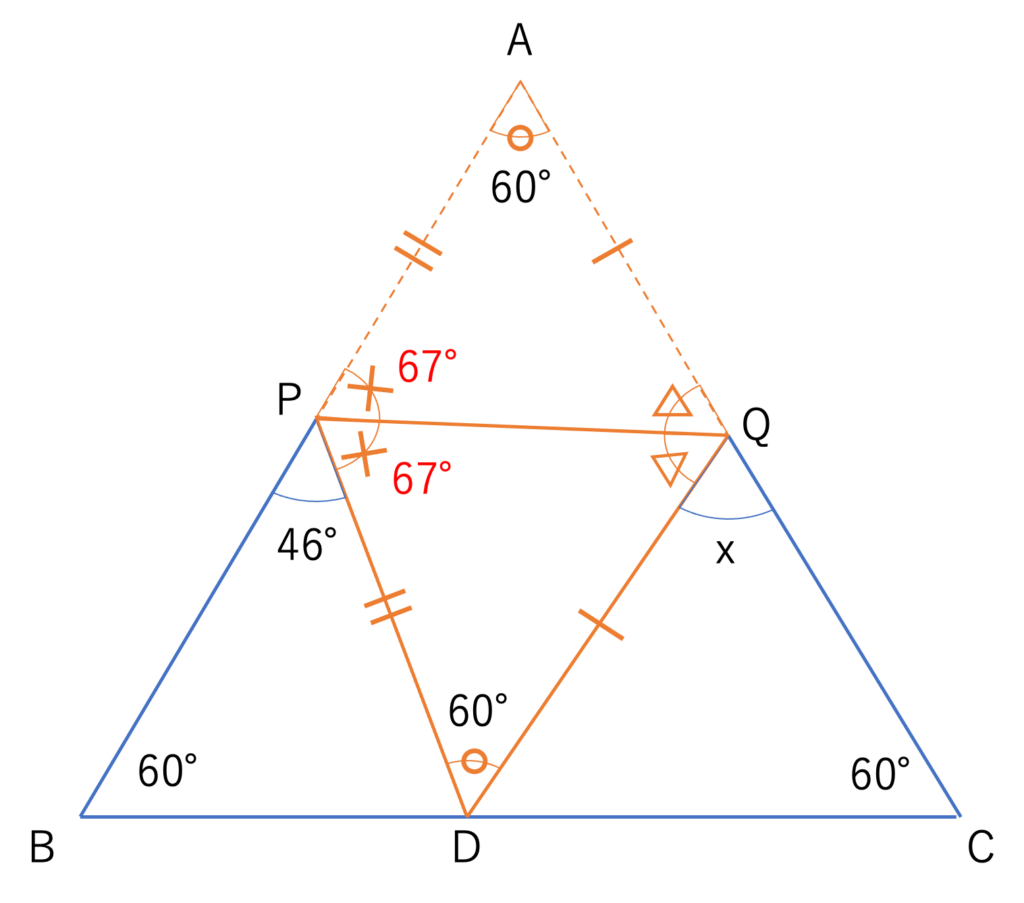
さて×の大きさが求められたところで,続いて注目するのは折り返しによって作られた三角形PQDです。
この三角形の1つの角は67°,もう1つの角度は60°だと分かっているので,値のわからない△の部分の大きさは180°-(67°+60°)=180°-127°=45°となります。
このとき線分PQを境に折り返された△が対応している角になりますので,その部分も53°だと明らかになりますね。
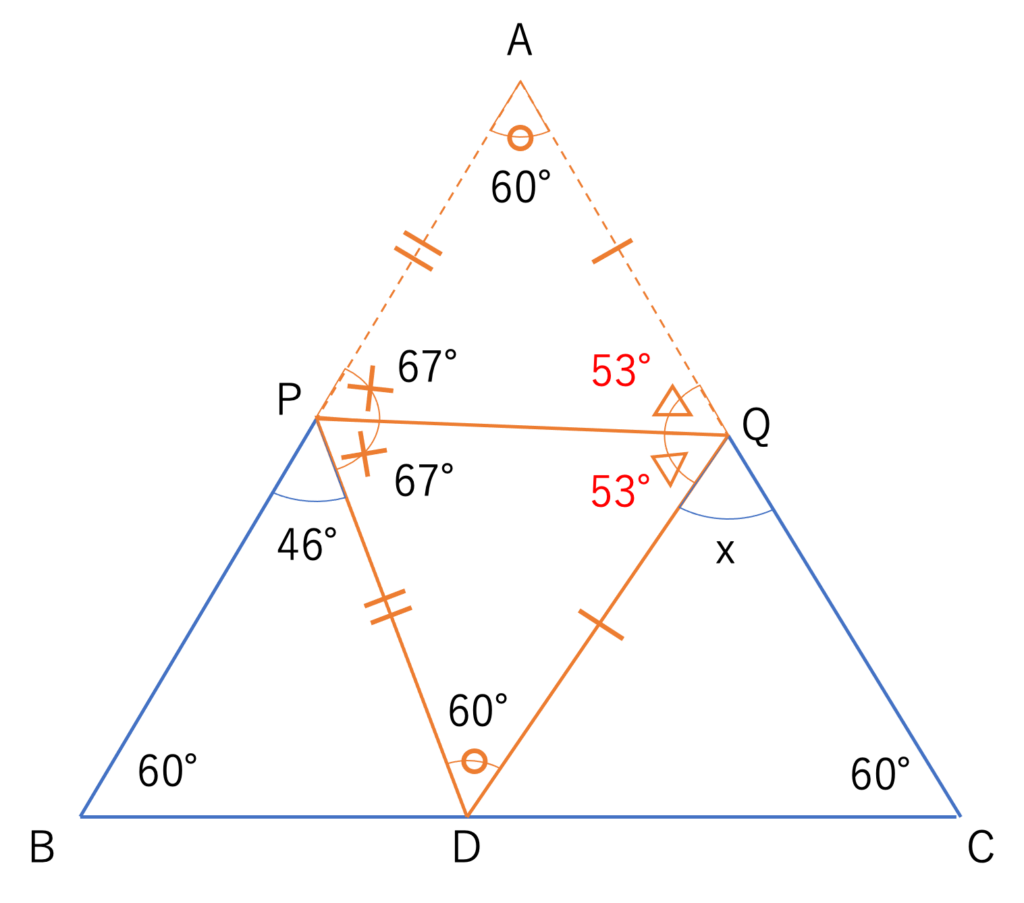
これらの情報からxの値を求めていきましょう。いまxが存在する線分に注目すると,この線分上には△の角度が2つとxがあることがわかります。このことから180°から△の角度2つ分を引けば答えに辿り着けそうだ,という予測ができますね。したがって答えは180°-(53°+53°) =180°-106°=74°となります。
A.74°
以上の解き方だと,解き方①で見たような点D周辺の角度の大きさは一切使いませんでした。ロスを避ける・無駄を省くという観点から見たとき,やはり受験算数では必要な部分だけを求めて計算するのが理想的だと言えます。
今回の問題ではどちらのルートでも必要な計算量は大差ないのですが,どちらを選択するにしろ,必要な分の情報だけで解き切るという意識を持って挑むと更なるレベルアップにつながりますので,日頃から他の問題でも意識してみましょう。
まとめ……の前に
登録6000人以上!
本サイト、中学受験ナビの監修も務めている『開成番長』こと繁田和貴が執筆する完全無料のメールマガジンでは、主に中学受験生のお子さんをお持ちの方へ向けた様々なお役立ち情報を配信中!
さらに今なら登録者にはもれなく「開成番長・繁田の両親が語る繁田の中学受験PDF」をプレゼント!
登録及び登録解除も簡単ですので、お気軽にご登録ください。

終わりに
今回の記事では図形の折り返しに関する入試問題にスポットライトを当て,基礎編でご紹介した内容を広げながら実践的な攻略方法をご紹介していきました。はじめにお伝えしたようにこの分野は一見難しく思われますが,細かく噛み砕いていけばそこまで難しくはありません。大切なのは臆病にならない心です,それを身につけるためにも以下のおすすめ記事や参考書籍を使いながら更なる演習に励んでいきましょう。本記事が今後の学習のお役に立てば幸いです。


















