2021.03.26 算数

直近2~3年の中学入試の出題傾向とその対策！【有名校編(偏差値50~60)】

本記事では【チャレンジ校編(偏差値65~)】，【難関校編(偏差値60~65)】の記事に続いて，有名校と呼ばれる偏差値50から60辺りの中学校の算数で出題された問題を分析していくものになります。なお今回引用するのは2020年度の問題が中心であるため，若干細かいトレンドの変更があるかもしれません。

このレベルの学校は，目標というよりは本命の滑り止めなどで受けられる方が多いと思うのですが，それでも油断してはいけません。安全校の対策がバッチリだからこそ，本命の勉強に集中できるのです。したがって傾向を抑え，その対策をしていくことは欠かせないでしょう。今回，出題の特徴は主に3つに分けられましたので，よろしければ引用する問題を解きながら読んでいただければと思います。

1つ目の出題傾向：単位変換・約束記号などの置き換えの問題

1つ目の特徴として挙げられるのが，とある数字を別の数字に置き換える問題です。これは文章だけだとわかりづらい問題だと思いますので，実際にいくつか例題を引用したいと思います。

下の□に当てはまる数を求めなさい。

2020113秒=□日□時間□分□秒

(淑徳与野中学校(2020)，一部改題)

次の□にあてはまる数を求めなさい。

時速17.4kmは，分速□mです。

(明治学院中学校(2020)，一部改題)

 

速度・距離・時間といったものにはいくつかの単位が存在します。このような単位の変換には，1km=1000mといった単位同士の結びつきの理解はもちろんのこと，計算ミスがないように慎重に取り組む姿勢も大事になってきます。また中には次のような約束記号を使った置き換えの問題も見受けられました。

△が3個集まると□1個に置き換え，□が3個集まると○1個に置き換え，○が3個集まると☆1個に置き換えます。☆☆○□□□△は，△いくつ分ですか。

(埼玉栄中学校(2020)，一部改題)

 

このような不思議な問題も単位の変換の問題と本質は同じであるため，有名高レベルで登場してもおかしくはありません。以下ではこのような置き換え問題への対策法をご紹介します。

置き換え問題の対策法は？

それでは単位の変換問題の解き方や対策法をご紹介いたします。まず大事なのは，使われている単位を一つの式で表すことです。例えば初めに引用した問題では日・時間・分・秒という単位が登場していました。これらは次のように整理できます。

1日=24時間=24×60時間=24×60×60分=24×60×60×60秒

1日=24時間=1440時間=5184000秒

このようにすべての単位についての関係性を明らかにできれば，与えられた秒数の中に1日がいくつあるのかを計算し，そのあまりの中に1時間が何個あるか計算し…と言った具合で答えを求めることができます。したがってこの式を作ることが置き換え問題の解き方になるのです。3番目の一見複雑そうな問題も，関係性を次のようにまとめられれば簡単に解けそうですよね。

☆=3×○=3×3×□=3×3×3×△

☆=3×○=9×□=27×△

この，式に関係性をまとめることは簡単そうに見えても，計算が複雑でミスが起きやすいため，何度も同じような問題を繰り返し，関係性を覚えるくらいまで式をひたすら作っていくことが重要です。単位についての問題はそこまでバリエーションが豊富なわけではないので，反復演習を重ねることで対策することをオススメします。

2つ目の出題傾向： 食塩水の濃度に関する問題

2つ目の出題傾向は，食塩水の濃度を計算する問題です。中学受験と言われてパッと思いつくくらいには，濃度に関する問題はメジャーなものなのではないでしょうか。例えば次の中学校の算数の入試問題において，濃度の問題が確認できました。

こさが6.4%の食塩水が200gずつ入っているA，B，Cの3つの容器があり，次の操作をします。

  • ①Bの中の食塩水に，さらに1.5gの食塩を溶かす
  • ②Cの中の食塩水から100gの水を蒸発させる
  • ③①と②の操作でできた食塩水をAの中の食塩水の中に混ぜる

このとき，③の操作後にAに入っている食塩水の重さは何gですか。小数第2位以下を切り捨て，小数第1位まで答えなさい。

(函館ラ・サール中学校(2020)，一部改題)

2つの容器A,，Bがあり，Aには400g，Bには500gの食塩水が入っています。Aから100gの食塩水をBに移した後，Aに200gの水を加えたところ，Aは6%，Bは7.9%のこさになりました。A，Bのはじめの食塩水のこさはそれぞれ何%でしたか。

(西武学園文理中学校(2020)，一部改題)

この他にも，三田学園中学校などでも同じような問題が見受けられました。

【チャレンジ校編】【難関校編】を読んでいただいた方はお気づきかもしれませんが，実はこの濃度の問題はハイレベルな学校では出題されにくいのです。このことから本命として有名を受ける人はもちろん，滑り止めとして受ける方も，濃度の対策を怠ってしまうと簡単に周りと差をつけられてしまいやすいです。しかし逆にいえば濃度の問題をしっかり抑えていれば，その他の範囲はハイレベルな受験校対策で一緒に抑えられますので，安心して受験することができると言っても過言ではないでしょう。

濃度の計算の対策法は？

ではこのような濃度の問題にはどうやって対処していけばいいのでしょうか。

その対策法として，食塩の重さ・水の重さ・食塩水全体の重さを整理する能力を鍛えることが挙げられます。濃度の問題は一見難しそうにも思えますが，実のところ1つの水溶液ごとに3種類の重さ+濃度が出てくるだけなので，情報を上手に整理することができれば算数が苦手な子でも簡単に答えを導き出せるのです。

そしてこの情報を面積図やてんびん図にまとめることが，有効な攻略法だと言えるでしょう。濃度・重さを対応させ，1つの図にまとめるのです。例えば初めに出てきた6.4%の濃度の食塩水200gを面積図に表すと次のようになります。


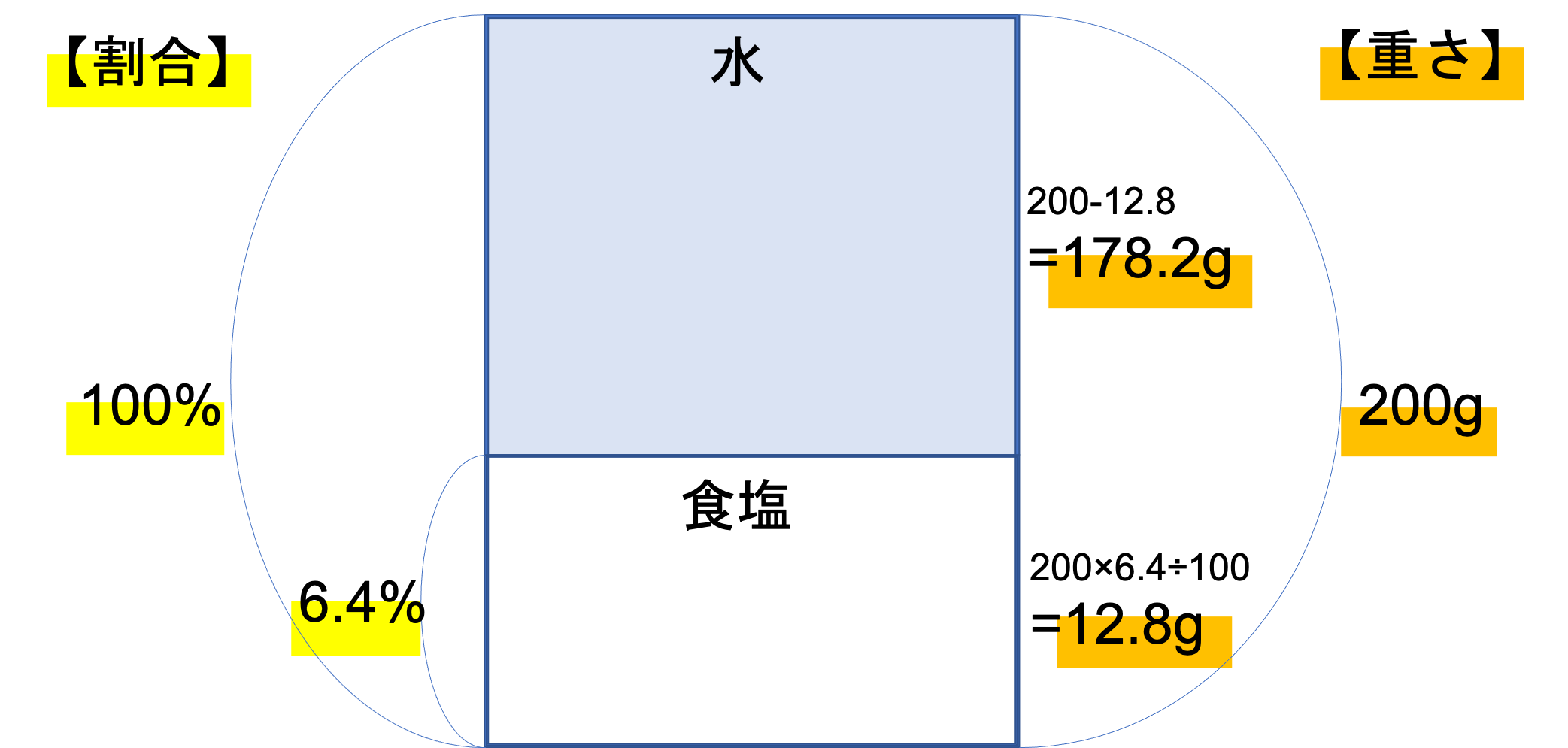
面積図にまとめると計算も行いやすいですよね。面積図や天秤図は色々な問題で活用できるので，この書き方をそのまま覚えてしまっても良いでしょう。

この情報を読み取って図に整理するということは一見難しそうでも，慣れてしまえば実は簡単です。特に食塩水の問題では，食塩水の重さなどの語句からどの数字が面積図のうちのどこを指しているのかがわかりやすいです。したがってたくさん問題を解くことで，まとめるという工程を自分のものにしていく必要があります。

ただし，濃度に関する問題を攻略するためには，応用問題にも積極的にトライしていくことも大事になってきます。先ほどご紹介した単位の変換問題とは違い，濃度の問題は応用されて複雑な形で出題されることもあります。

上で引用した2つの問題では2つ・3つの食塩水が出てきていました。となると当然4つ以上の水溶が登場する問題もあるのでは，と予測できます。あまりにも難しい問題は有名校では出てきにくいかもしれませんが，どんなに複雑な問題でも乗り越えられる応用力を身につけておくことは，濃度という単元において極めて重要です。レベルの高い問題をたくさん解き，応用力を身につけていく練習も同時に積み重ねていきましょう。(苦手かな?と思った読者の方は，こちらの記事をご一読ください。)

3つ目の出題傾向：形はカンタン・計算はフクザツな平面図形

最後にご紹介する出題のトレンドは，平面図形からの出題です。以前【難関校編】の記事でも平面図形からの出題が多かったと記述しましたが，有名校で登場していたのはその中でも，形はわかりやすいけど計算はややこしい図形が中心でした。この意味を理解していただくために，以下で2つほど問題をご紹介いたします。

下の図のように半径4cmの円が長方形にぴったり入っています。車線の部分の面積は何cm2ですか。

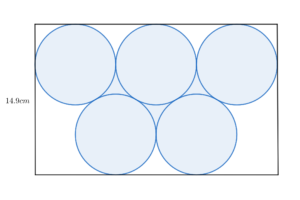
(淑徳与野中学校(2020)，一部改題)

次の図のように，点Pを中心として直線より下に4つ，点Qを中心として直線より上に3つの円を描き，PとQ，RとSを線で結び色をつけました。色のついた部分について，周の長さと面積を求めなさい。ただし，PQとRSの長さは1cmとします。

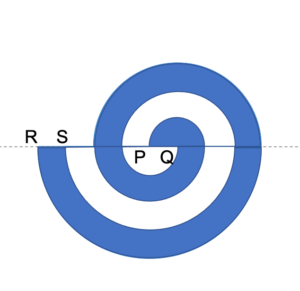
(埼玉栄中学校(2020)，一部改題)

これらの問題はどれも，【難関校編】で紹介したものに比べると，よりわかりやすくて単純な構造をしていることに気づくと思います。例えば上の図形は四角形と丸とで出来ていますし，下の図形は半円の組み合わせで出来ています。これが形はカンタンの意味になります。

しかしこれらの問題は計算がややこしいです。上の図形の面積を求めるならば，まず円5つ分の面積を求めるのですが，その次に円3つの周で出来上がる歪んだ三角形を求めなければなりません。

受験算数に慣れている人であれば，この部分は3つの中心を繋いでできる三角形から扇形3つ分の面積を引くことで求められると予測できますが，慣れていないと計算のテクニックは思いつきづらいかと思われます。

計算が難しい平面図形の対策法は？

では計算が難しい図形にはどのように対策していけばいいのでしょうか。

このような図形の計算の難しさは，先ほど述べたように，計算のテクニックが思い浮かばないことが挙げられます。以下では計算方法を素早く思いつくための対策法をご紹介します。

計算方法を思いつくために大事なのは，図形の組み合わせとして問題を眺めることです。この図形の組み合わせについてはおすすめ記事の中でも触れられているので，詳しくはその記事を読んでいただければと思います。軽くご説明しますと，例えば上の問題で言えば，円5つと歪んだ三角形や半円の集まりとして図形の面積を求められそうだという見方が，出題された図形を基本的な図形の集まりとして眺めるというものになります。

このような捉え方を鍛えていくには，基本レベルの問題から応用レベルの問題まで，難易度を問わず様々な問題を解いていくことが有効かと思われます。難しい問題ばかりやっていても苦戦することが多いでしょうし，なによりその難しさゆえにみんな知っているから二度と問題として出されない可能性もあります。しかし基礎的な問題ばかりやっていても応用力は身につきません。いろんなレベル感の問題をバランスよく解いていきましょう。

まとめ

本記事ではこれまで，有名校と呼ばれる偏差値50~60あたりの中学校の入試問題を取り上げ，その特徴を攻略法・対策法とともにご紹介していきました。改めて今回取り上げた内容を最後にまとめると，次のようになります。

  • 単位の変換・置き換えという傾向→関係性を整理する演習の繰り返しで対策！
  • 濃度の計算という傾向→図にまとめる演習と応用問題への挑戦で対策！
  • 計算が複雑な平面図形という傾向→図形を分割する思考を様々な問題を解くことで対策！

これらの傾向はどれも有名校独自のものですので，本命として・滑り止めとして，に関係なく，1校でもこのレベルの学校を受けるお子様のいる家庭の皆様に参考にしていただけたら，と考えております。本記事が第一志望合格の手助けとなれば幸いです。よろしければ以下ご紹介するおすすめ記事も一読していただけたらと思います。

(ライター：大舘)

おすすめ記事

参考

 

RECOMMENDこちらの記事も人気です。