今回の記事では調べ・推理・計算の条件に関する分野を解説していくシリーズの第3本目として，魔方陣に関する問題の解き方をご紹介していきます。この魔方陣に関する問題は低学年のお子様でも取り組みやすいので，受験を志している方はもちろんのこと，算数の成績を伸ばしたい・算数を好きになってもらいたいとお考えの低学年のお子様を持つ保護者の方にも読んでいただきたいです。
Contents
魔方陣とは？
それではここからは魔方陣に関する問題の解き方について解説していきます。まずは魔方陣とは何か，という前提知識を抑えておきましょう。簡潔に言ってしまえば，魔方陣とは数字が配置された正方形のマス目のことを指します。ただこの数字というのはランダムに並べられているのではなく，たてとよこと斜めのどの列についてもその合計が同じになるように並べられています。小学校で習うレベルの問題だと3×3のマス目が登場することが一般的ですが，問題によっては4×4のマス目が登場してきたり，3×3のマス目がいくつも組み合わさった形で登場してきたりします。今回は3×3の合計9マスの場合の魔方陣について考えていきますが，基本の解き方を覚えておけば応用問題も問題なく解くことができますので，まずはこの記事を通して基本の形の魔方陣についての理解を深めていきましょう。
魔方陣の問題を見てみよう！
それでは魔方陣がどんなものかを理解していただいたところで，実際にいくつか魔方陣の問題をご紹介していきましょう。受験で登場するような問題だともっと情報が制限されていたりするので難しく感じるかもしれませんが，前述したようにまずは基本の形を解いて魔方陣というものの解き方に慣れていきましょう。
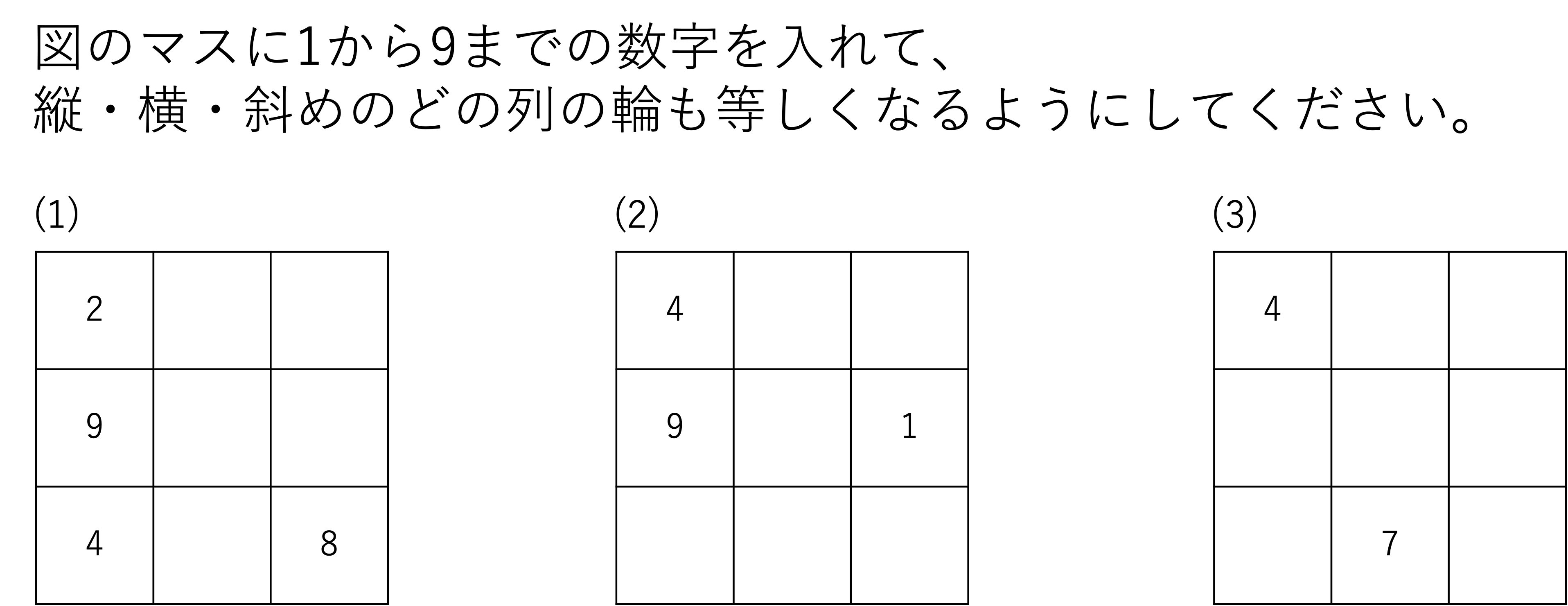
このように中学受験に登場する問題はマス目の中の一部が公開されていて，その情報をもとに残りのマスの中身を推定していくという流れで解くように作られています。(1)は優しめ・(2)は平均的・(3)は難しめな問題になっていて、(2)程度の問題を一人で解けるようになることが理想です。まずは解き方の解説として、(1)の問題を使いながら問題を解く糸口を掴んでいきましょう。
魔方陣を解くには…？
まずは列の和を考えてみよう！
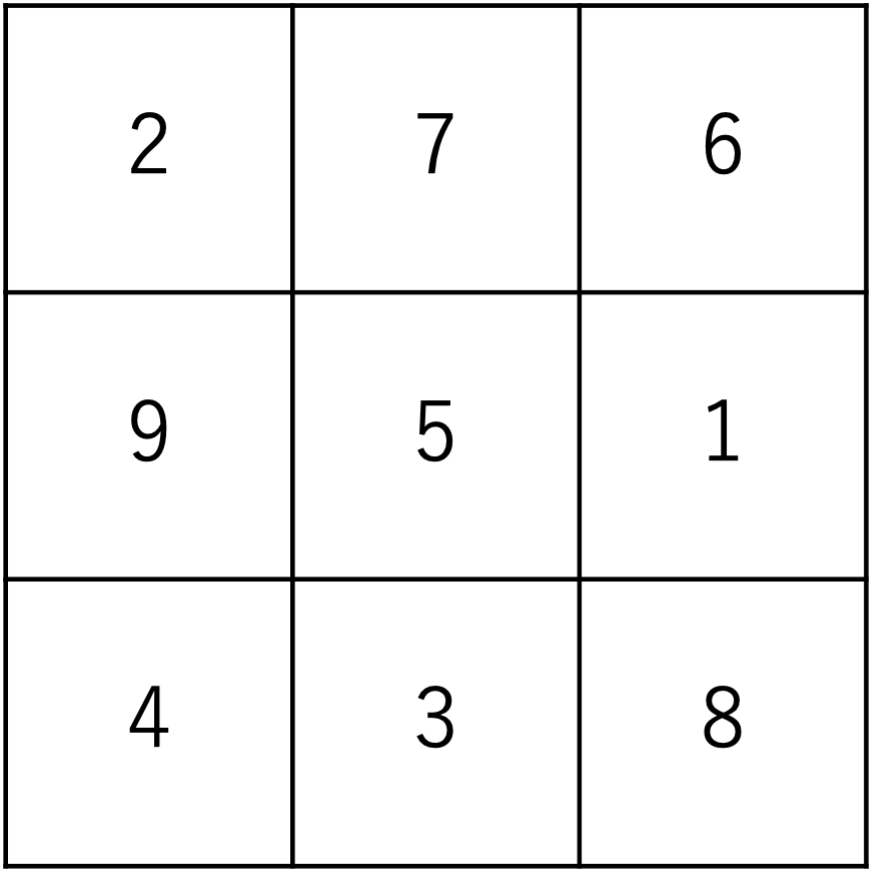
それではここからは先ほど紹介した(1)の問題を使いながら，魔法陣の攻略方法を学んでいきましょう。改めて先ほどの問題をここでご紹介しておきます。
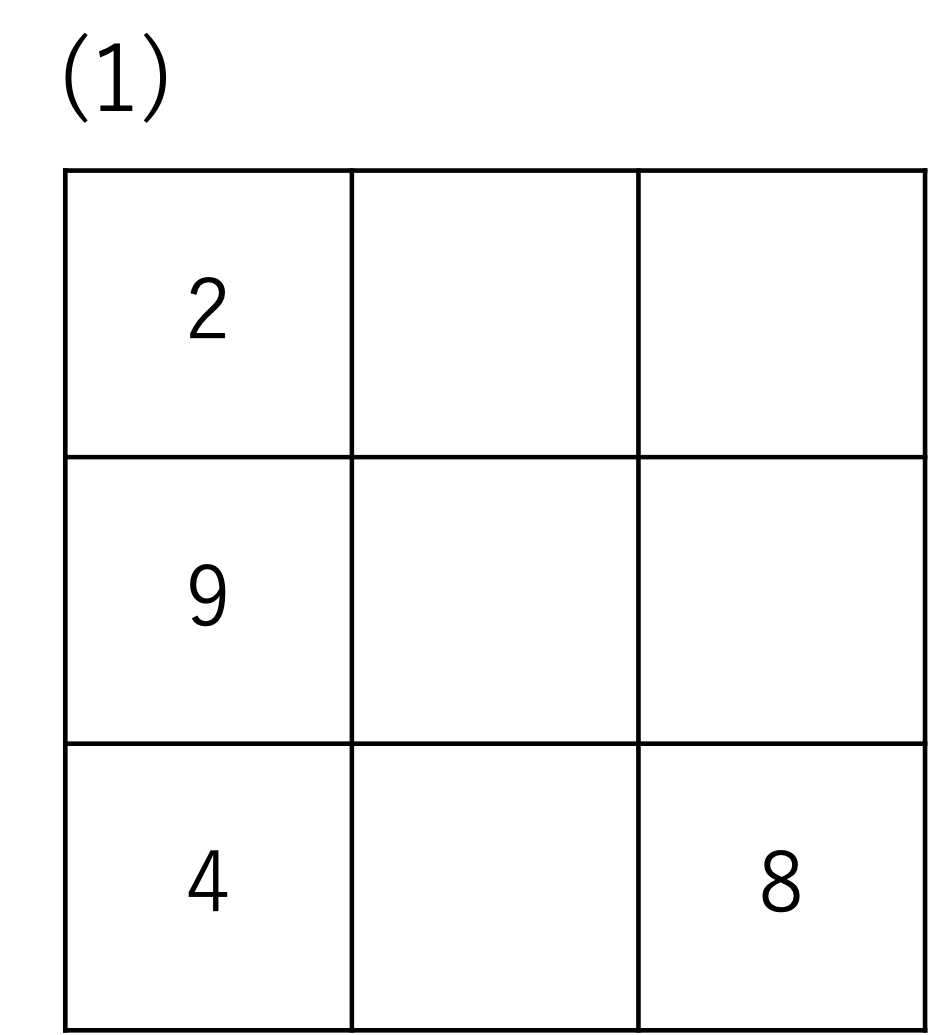
まず問題を解く上で重要なことが，この魔方陣における各列の和を計算することです。今回の問題は一番左側の列が埋まっているので，全ての列の和は2+9+4=15になっていることが分かります。ただし問題によっては全てのマスが埋まっている列が存在しない場合もあるので，自分で確かめていく必要があります。その点には注意しておきましょう。
ちなみにこの問題のように1から9までの数字を当てはめていく問題の場合，各列の和は15になります。というのもそれぞれの列の和を足していった場合，各列の和は全ての数字の合計の3分の1になるからです。そして1から9までの全ての数を足した合計は45なので，それぞれの列の数字を足し合わせた合計は45÷3=15になるということです。中学受験に登場するほとんどの魔方陣は，1から9までの数字を3×3のマス目に入れる構成をしていることが多いです。もちろん自分の頭と手で話を考えていくことも重要ですが，基本的に15になると覚えてしまうと計算がスムーズになるでしょう。
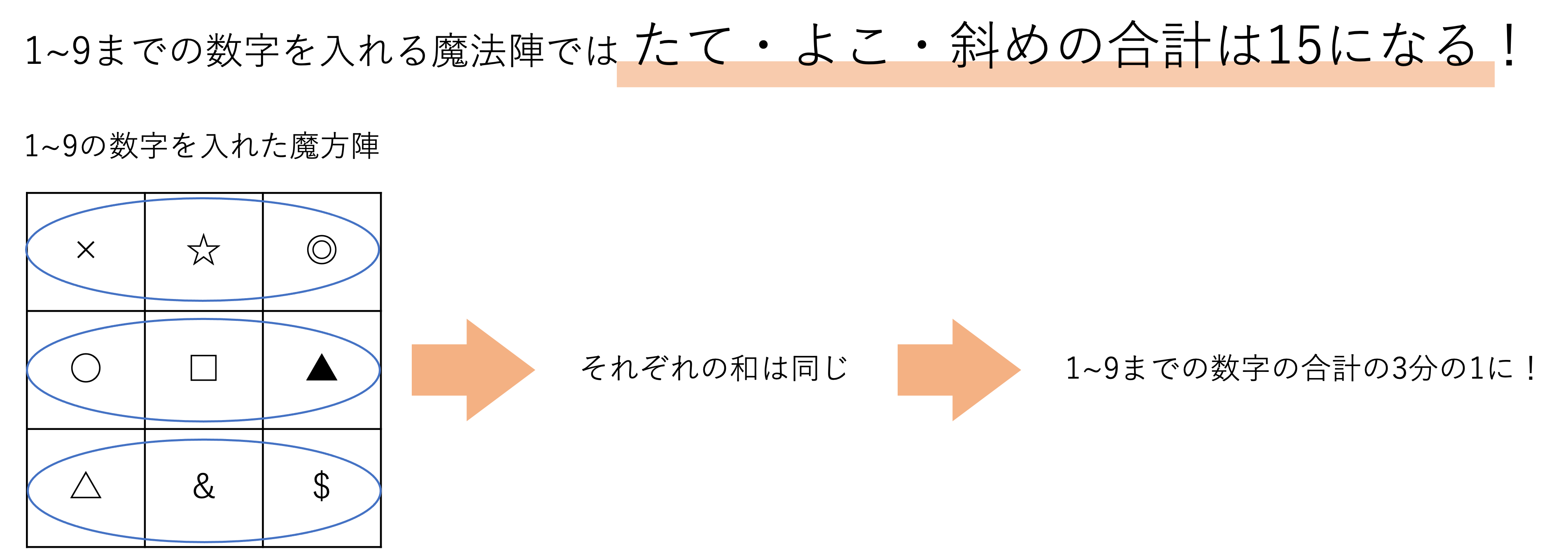
なおこのことから転じて，たて○マス・よこ○マスの魔方陣における各列の和は当てはめるべき数字の総和の○分の1になると言うこともできます。3×3マス以外の魔方陣はめったに目にしないですが，ぜひ覚えておきましょう。
1個だけ埋まっていない列に注目しよう！
さてこのように問題から・推測からそれぞれの列の和が計算できたところで，そのヒントをもとに全てのマス目を埋めていく必要があるのですが，ここで重要なポイントが，1マスだけ埋まっていない列に注目していくということです。今回であれば一番下に存在する4と8が記入されている列を見ていきましょう。の一番下の列には現在4と8が書かれていて，その総和は4+8=12になるため，各列の和である15になるには3足りないと判断することができます。そのため真ん中の一番下のマスには3が記入できますね。このように1つ空いている列に注目しながら，1つずつ順番に穴を埋めていきましょう。
残りは穴埋めの繰り返し！
ここまで各列の和を求めた上で1つ穴を埋めていきましたが，あとはこの工程を繰り返すことで全てのマスを埋めることができます。続いて埋められそうなものは2と8で挟まれた斜めの列ですね。この列の合計も15になるのですが，今2つの数字の合計は2+8=10となるので5足りないことが分かります。それゆえ真ん中には5が入ると明らかになります。
そして残りの3つのマスはたて・よこ・斜めのラインに注目することで同じように求めることができますね。真ん中のたての列に注目すると5+3=8で15になるには7足りないので真ん中の上には7が，右上がりの斜めの列に注目すると5+4=9で6足りないので右上には6が，真ん中のよこの列に注目すると9+5=14で1足りないので右の真ん中には1が入ると計算できます。このように1個ずつ着実に計算していくことで，マス目は次のように埋めることができました。1個だけ空いている列はどこか，と目を凝らすと答えを求めることができるので参考にしてみてください。
練習問題を解いてみよう！
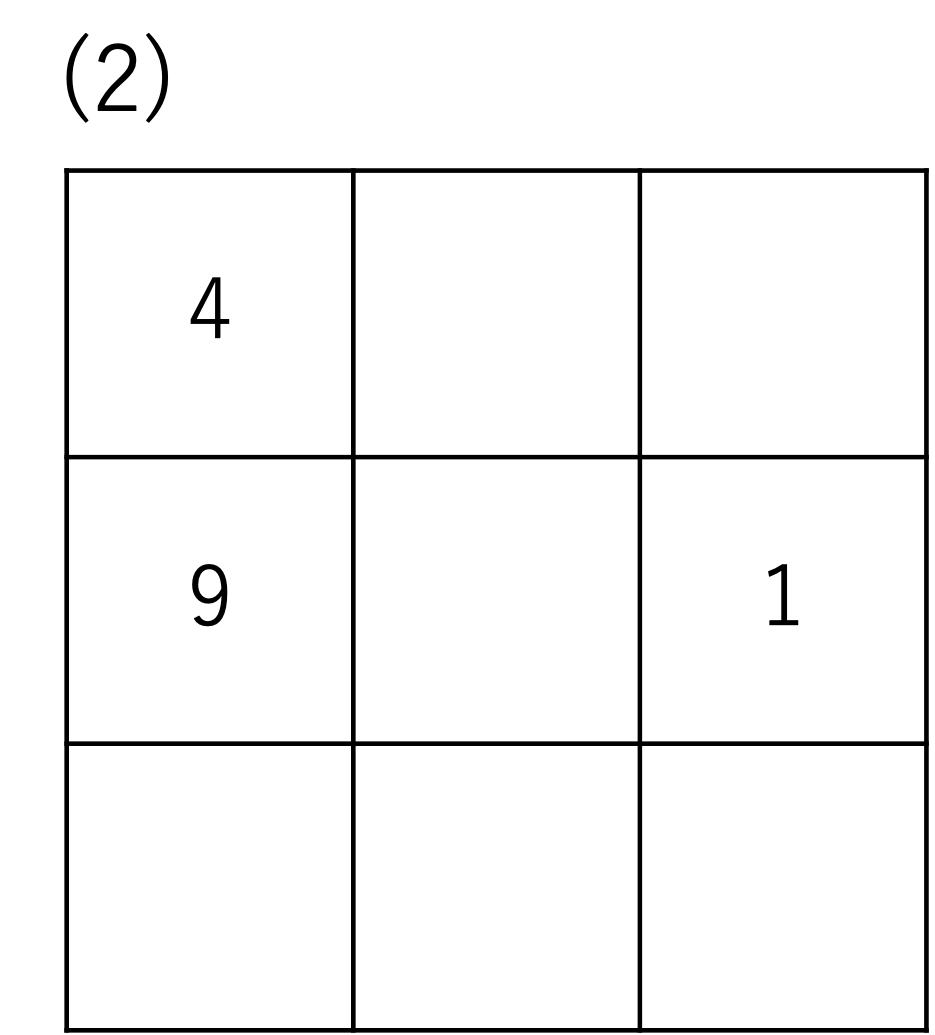
それではここまでお教えしたことを参考に練習問題を解いていきましょう。ここでは先ほどご紹介した問題のうち、(2)を使いながら知識の定着を狙っていきます。改めて問題を載せておきますので，まずは自力で解けるかどうか試してみてください。
練習問題解説
それではここからは上でご紹介した魔方陣の解説に移ります。まず初めに大切なことが，この魔方陣には1から9までの数字が入るということの確認です。この前提があることで，先ほども説明したような各列の和が15になるということを基にして問題と向き合うことができます。問題によっては1~9以外の数字が当てはめられている場合もあるので，どんな数字が入るのだろうと確認しながら解いていかないと大きなミスに繋がってしまうこともあります。確認の作業は忘れないようにしましょう。
さて，前提条件を問題文から確認できたところで，あとはセオリー通り1つ足りないマスから順番に埋めていきましょう。まず埋められそうなのが左端の1列と真ん中の横1列ですね。左側には今4と9が配置されています。これらの和は4+9=13なので，左下には2という数字を書き込むことができます。これと同じ要領で真ん中の列にも注目すると，現在埋められている9と1を足し算した結果は9+1=10となるので，中央には5が書き込めます。このようにひとつひとつマスを埋めていくことが魔方陣の計算では重要です。ここまでの内容を整理すると，次のようになります。
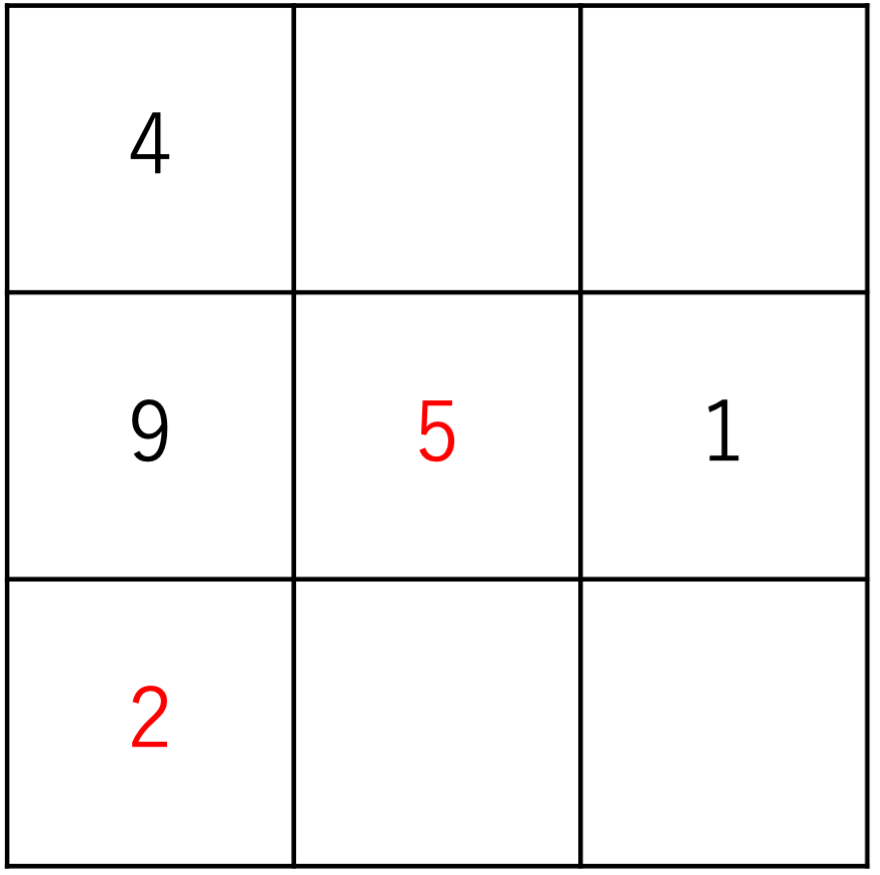
あとは同様の手順を踏んで残りのマスを埋めていけば問題を終えることができます。まず斜めの列から見ていきましょう。右上がりの列は現在5と2が記入されているので15-(5+2)=8より右上には8が，右下がりの列は現在4と5が記入されているので15-(4+5)-6より右下には6が当てはまります。
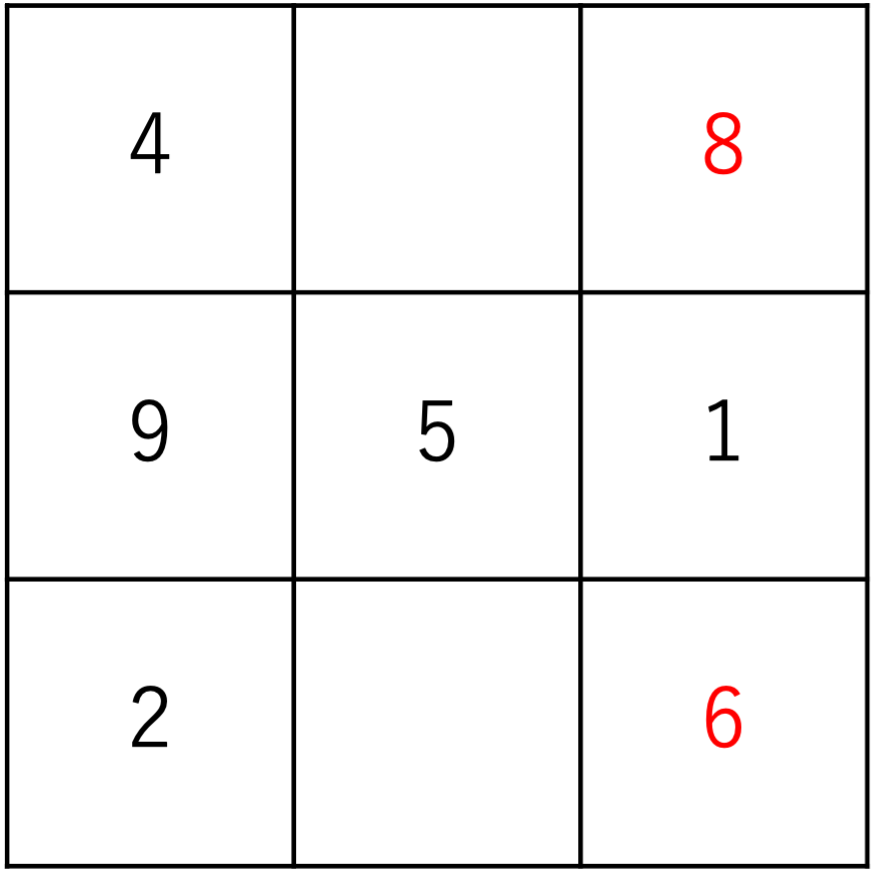
残るは2マスとなりましたが，先に真ん中上のマスから見ていきましょう。このマスを含めたよこのラインに注目すると，両隣には4と8が存在することがわかります。そしてこの2つの数字の和は4+8=12なので，このマスには3が入ることが分かります。最後に真ん中下のマスですが，ここには両隣に2と６が入っていることから，15-(2+6)=7が書き込めることが分かりますね。最後に残ったマスについては計算して求める方法の他に，1から9までの中でまだ登場していない数字を探す方法も存在します。どちらでも精度はさして変わりませんので，分かりやすい・解きやすい方の手段で答えを導いていただければ幸いです。
以上の手順を踏むことで上のような魔方陣が導かれました。このように，ひとつひとつの簡単なステップをしっかり踏んでいけば魔方陣は問題なく解くことができます。しかし受験本番では何が起こるか分かりません。試験のタイミングで本領を発揮できるように，算数が得意な人も魔方陣の問題には慣れておくといいでしょう。
まとめ……の前に
登録6000人以上！
本サイト、中学受験ナビの監修も務めている『開成番長』こと繁田和貴が執筆する完全無料のメールマガジンでは、主に中学受験生のお子さんをお持ちの方へ向けた様々なお役立ち情報を配信中！
さらに今なら登録者にはもれなく「開成番長・繁田監修 中学受験必勝の5箇条PDF」をプレゼント！
登録及び登録解除も簡単ですので、お気軽にご登録ください。
まとめ
今回の記事では魔方陣の性質を紹介した上で，その出題傾向や解き方をご紹介していくものでした。この魔方陣という問題は前述したように小学校低学年のお子様でも解きやすく，頭の体操としてピッタリの分野です。しかしそういう範囲の問題に限って，本番になると焦って解けなくなってしまいがちです。他の分野の問題の対策を進めるのと並行して，条件の整理に関する問題も完璧にしていきましょう。本記事が今後の学習のお役に立てば幸いです。
