本記事では和差算の応用問題を取り上げて,解き方をご紹介していくものです。和差算は小学校で習う算数で最も基本的な部分ですが,応用問題への対処法は案外教わらないものです。一緒に学んでいきましょう。
応用問題を取り扱うという内容上,ある程度和差算についての理解が必要です。もちろん導入部で改めて説明しますが,和差算が何か聞いたこともない!という方は是非,おすすめ記事の欄にあるものを一読いただければと思います。
和差算とは?
では最初に和差算とは何かについて軽く触れておきましょう。和差算とはその名から分かる通り,計算の和と差,つまりは足し算と引き算とを使って解く問題のことを指します。
そして足し算・引き算を使って解けるという性質から,他の特殊算や図形問題に比べるとあまり詳しく解説されない傾向にあります。
しかし,このような和差算であっても受験に出てくるということは対策が欠かせません。和差算の解き方を押さえておくのは,合格のために大いに意味があります。
和差算の解き方!
それではここからは和差算の解き方について,例題を交えつつ復習していきましょう。
りんごとみかんがいくつかあります。りんごはみかんより3個多く,全部で15個あります。りんごとみかんはそれぞれいくつあるでしょう。
これが初歩的な和差算の問題になります。おそらく似たようなものを学校で見たことも多いでしょう。難しく感じる人でも時間をかければ解ける,そんな問題です。ではここからはこの例題を使って,どんなレベルの問題でも通用する和差算の攻略法をご紹介していきます。
まず抑えなければいけないのは,和・差の中身の確認です。問題によっては和が〇〇,差が××という形で書かれていなかったりするので,問題のどこが和・差に対応するのかをあらかじめ確認しておきましょう。今回はりんごの数とみかんの数の和が15個,りんごの数とみかんの数の差が3個ということが読み取れます。りんごの方が多いことにも注意しておきましょう。
次にこれを図に表してみることが重要です。和差算では一般的に線分図を書くことが多いです。和が15個・差が3個という情報をふまえて図を書くことを意識しましょう。
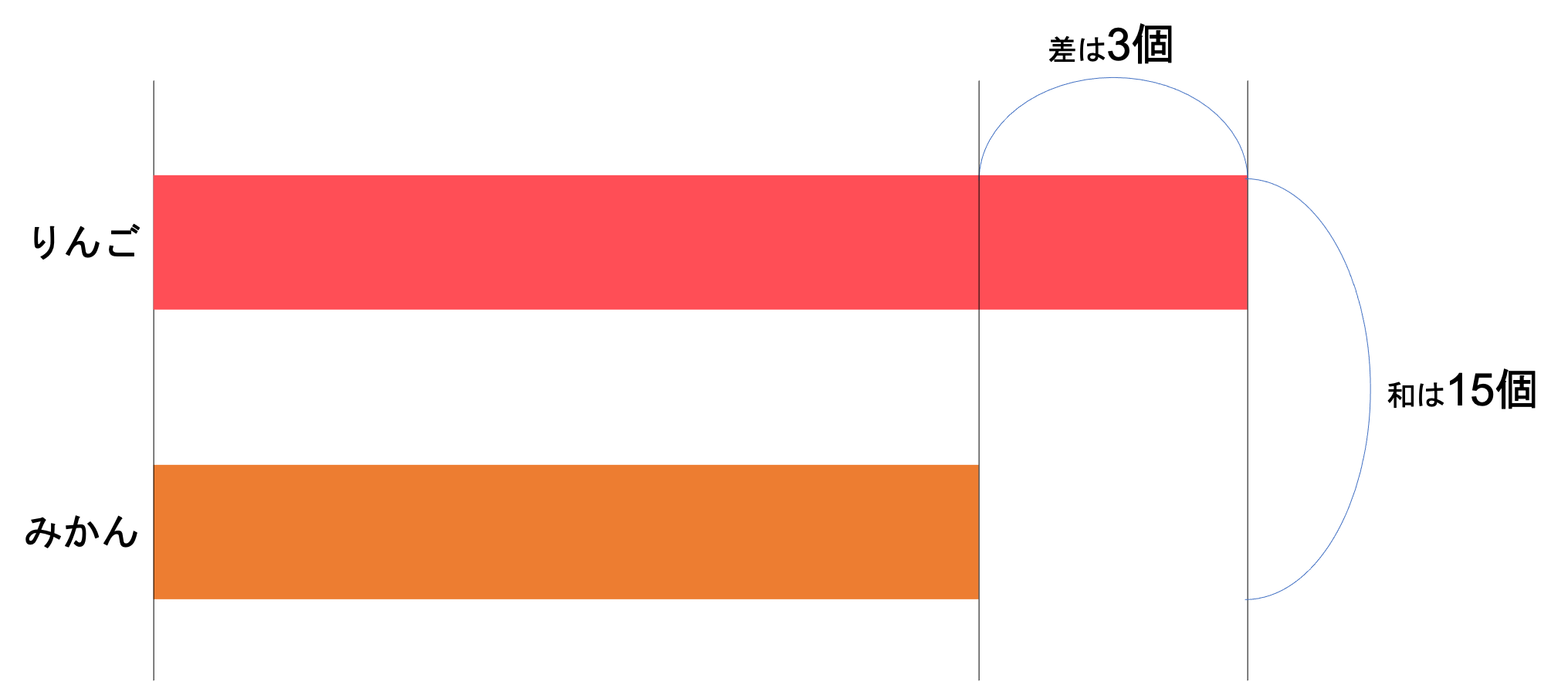
上のような線分図を書くと,和と差からどのように計算していけばいいかがわかりやすいですね。りんごの方が3つ多いということは,りんごの数から3を引くとみかんの数と等しくなるということを指します。いま15個のうち3個がりんごだと確定していることから,15-3=12個を半分にしたものがみかんの数だ,と判明するわけです。
このことからみかんの数は6個・りんごの数は6+3=9個だと分かります。以上が例題の答えです。和差算を解くときは,①和と差の中身に気をつけ,②線分図に表すとこのように計算しやすいです。どのような問題でもこのテクニックは有効なので,下の問題を解くときにも参考にして欲しいです。
応用問題を解いてみよう
それでは,上の章で復習した知識を使って,実際に入試に出てきた問題を解いてみることにしましょう。初めの一問は比較的簡単なものを引用しましたので,是非一度解いてみてください。
4つの整数A,B,C,Dがあります。AとBとCの和は210,AとBとDの和は195,AとCとDの和は223,BとCとDの和は206です。このとき,Aはいくつですか。
(豊島丘女子学園中学校(2021),一部改題)
いかがでしょうか。解けた人・解けなかった人どちらもいると思います。2つの数の和や差について聞かれたことはこれまであっても,4つの数の和や差が登場することは滅多にないでしょう。このような問題に対応することが昨今の中学入試では問われています。
ただ,もし解けなかった場合でも気にする必要はありません。和差算は応用のパターンが少ないため,解けない・知らない問題と出会ったら,パターンの網羅に近づいた!と考え方を変えてあげるといいでしょう。
解説
それではここからは問題の答え合わせをしていきます。上で述べたように,まずは和と差の正体に気をつけることが大事です。しかしこの問題では和が〇〇・差が××のように示されているため,次のステップに進むことにしましょう。
次は,問題の条件を図に整理していきましょう。A・B・C・Dの4つの数の関係をまとめると,下の図のようになります。
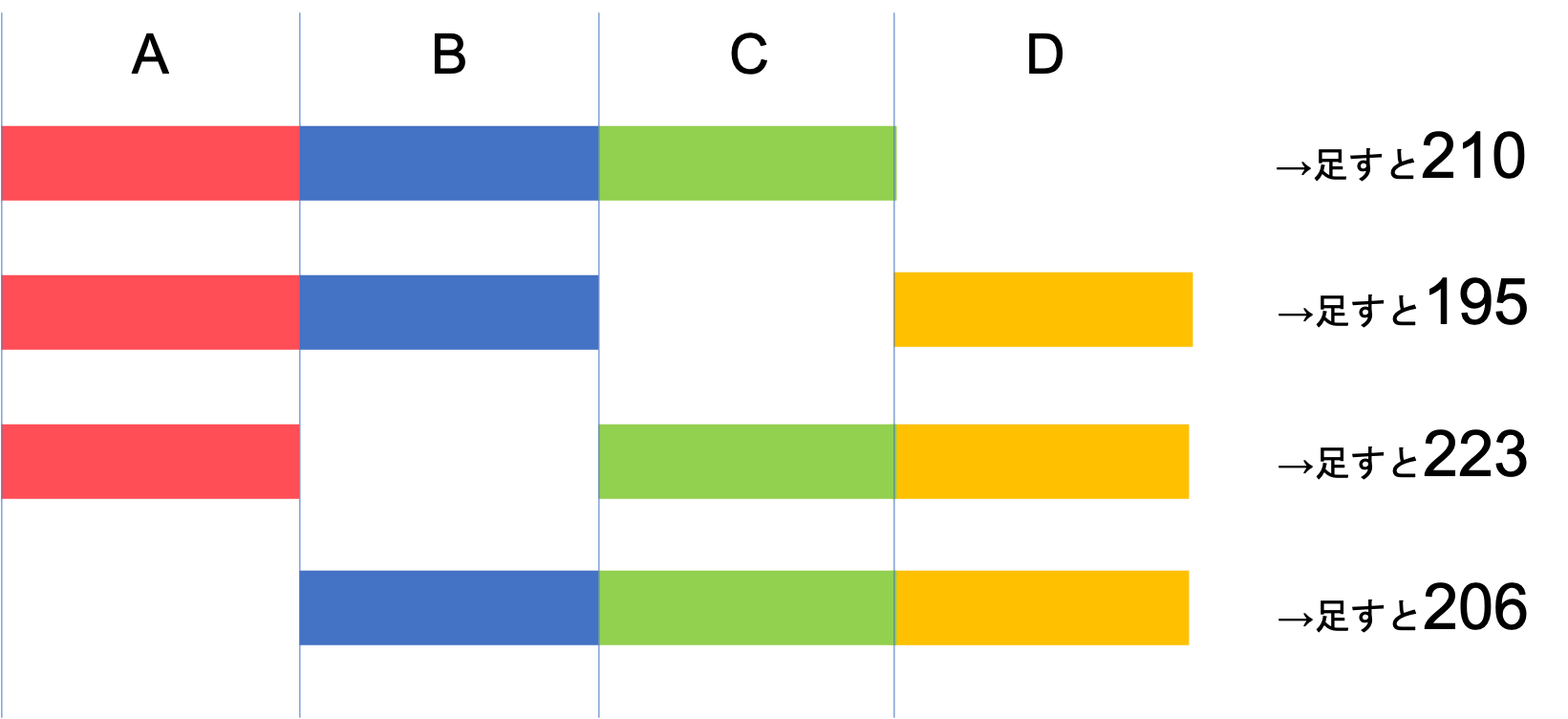
この図をもとに考えていきます。いま提示されているのは3つの数の和ですね。先ほどのように2つの数の和が出ているわけではないので,このままだと考えづらいです。そのため3つの数を1つのかたまりとみなし,足したり引いたりして手掛かりを探りましょう。
例えば,A・B・Cの和を足すと210, A・B・Dの和を足すと195になるわけですが,このことからAを2つ・Bを2つ・Cを1つ・Dを1つ足すと210+195=405になることが分かります。このような手順を繰り返します。
Aを2回・Bを2回・Cを1回・Dを1回足した数字にさらに,B・C・Dの和を足すと405+223=628になります。ここでA3つ・B2つ・C2つ・D2つの和が628とわかりました。ここでB・C・Dを同じ数だけ足しているため,この和からB・C・Dの組の和を引けばAのみに関する和を考えられそうですね。
問題よりB・C・Dの和は206ということが分かっているため,B2つ・C2つ・D2つの和は206+206=412ですね。
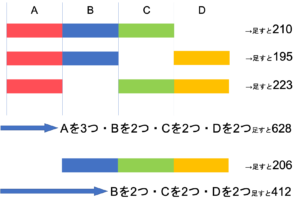
したがって次の数式が成立します。
(A3つ・B2つ・C2つ・D2つの和)-( B2つ・C2つ・D2つの和)=A3つ
このことから628-412=216がAを3回足した数字と判明します。よってAの値は,
\(216\div3=72\)
だと明らかになりましたので,Aの数値を活かして他の数字についても考えましょう。

このB・C・Dの3つの和だと,それぞれの値を求めることができる人も多いのではないでしょうか。今回上にある3つが2つの数字の和であり,加えてBとCとDの和も分かっているため,順番に差を求めてそれぞれの値を求めていきます。まずB・Cの和が138であることから次の数式が成立します。
(B・C・Dの和)-( B・Cの和)=D
したがってDの値も206-138=68とわかります。続いてB・Dの和が123であることから次の数式も成立しますね。
(B・C・Dの和)-( B・Dの和)=C
このことからCの値は206-123=83です。最後C・Dの和が152なので,
(B・C・Dの和)-( C・Dの和)=B
という数式から,Bの値は206-151=55となります。以上のことからA=72,B=55,C=83,D=68が答えになります。最後に確かめ算としてこれらの値を実際に足して計算を終わりにしましょう。
A+B+C=72+55+83=210
A+B+D=72+55+68=195
A+C+D=72+83+68=223
B+C+D=55+83+68=206
答え.A=72,B=55,C=83,D=68
まとめ
今回は和差算について,基礎的な問題の解き方から応用問題への攻略法までを取り扱いました。今回ご紹介した応用問題はほんの一部ですが,前述したように和差算の応用は限られているため,少しずつパターンを網羅していきましょう!本記事が学習の手助けとなれば幸いです。
(ライター:大舘)
おすすめ記事
参考
- 小学4年生までに身につけたい 和差算の思考センス,文英堂(2011)
- 文章題和差算・分配算―小3レベル,認知工学(2005)
- 強育パズル たし算計算ブロック 初級編,ディスカヴァー・トゥエンティワン(2013)