今回は「分配算」の解き方を解説していきます。
線分図の書き方や分配算の基本的な考え方は「和差算の記事」を読むとわかりやすいので、不安な方はぜひそちらから読んでみてください。
Contents
分配算とは
分配算とは、ある物を配ったり、分けたりしたときにどのように分けたかを求める問題です。
これだけ聞くと和差算と似ていますが、「和と差」だけで問題が解ける和差算と違い、分配算では具体的な数値だけでなく、「比」も登場します。
そして、「和と差」と「比」という情報をもとに、どのように物が分けられたかを解いていきます。これだけだとわかりにくいので、実際に問題を見てみましょう。
-
りんごとみかんが全部で37個あります。みかんはりんごの2倍よりも7個多いです。りんごとみかんはそれぞれ何個ありますか？
-
兄のおこづかいは弟のおこづかいの2倍よりも1000円多く、兄弟のおこづかいの合計金額は5500円である。兄と弟のおこづかいはそれぞれ何円でしょうか？
-
あめ玉が38個あります。これを太郎君と花子さんに分けると、花子さんのもらったあめ玉は太郎君のもらったあめ玉の3倍よりも2個だけすくなかった。2人は何個あめ玉をもらったでしょうか？
これだと想像がつきやすいのではないでしょうか。これが和差算の基本形です。それではさっそく問題を解いてみましょう。
分配算の解き方
まずは①の問題を実際に解きながら、和差算の解き方について解説していきます。
（問題①）りんごとみかんが全部で37個あります。みかんはりんごの2倍よりも7個多いです。りんごとみかんはそれぞれ何個ありますか？
このくらいの問題だと、線分図を書かなくても解けてしまうかもしれませんが、ここでは難しい問題でも使えるように丁寧に解説していきたいと思います。
線分図での解き方（問題①）
先ほどの問題をいきなり解くのは難しいかもしれないので、まず次の問題を解いてみましょう。
（問題☆）りんごとみかんが全部で30個あります。みかんはりんごの2倍の数です。りんごとみかんはそれぞれ何個ありますか？
この問題は分配算の中でも「比のみ」で解けるものです。まずはこの問題で線分図を書いてみましょう。
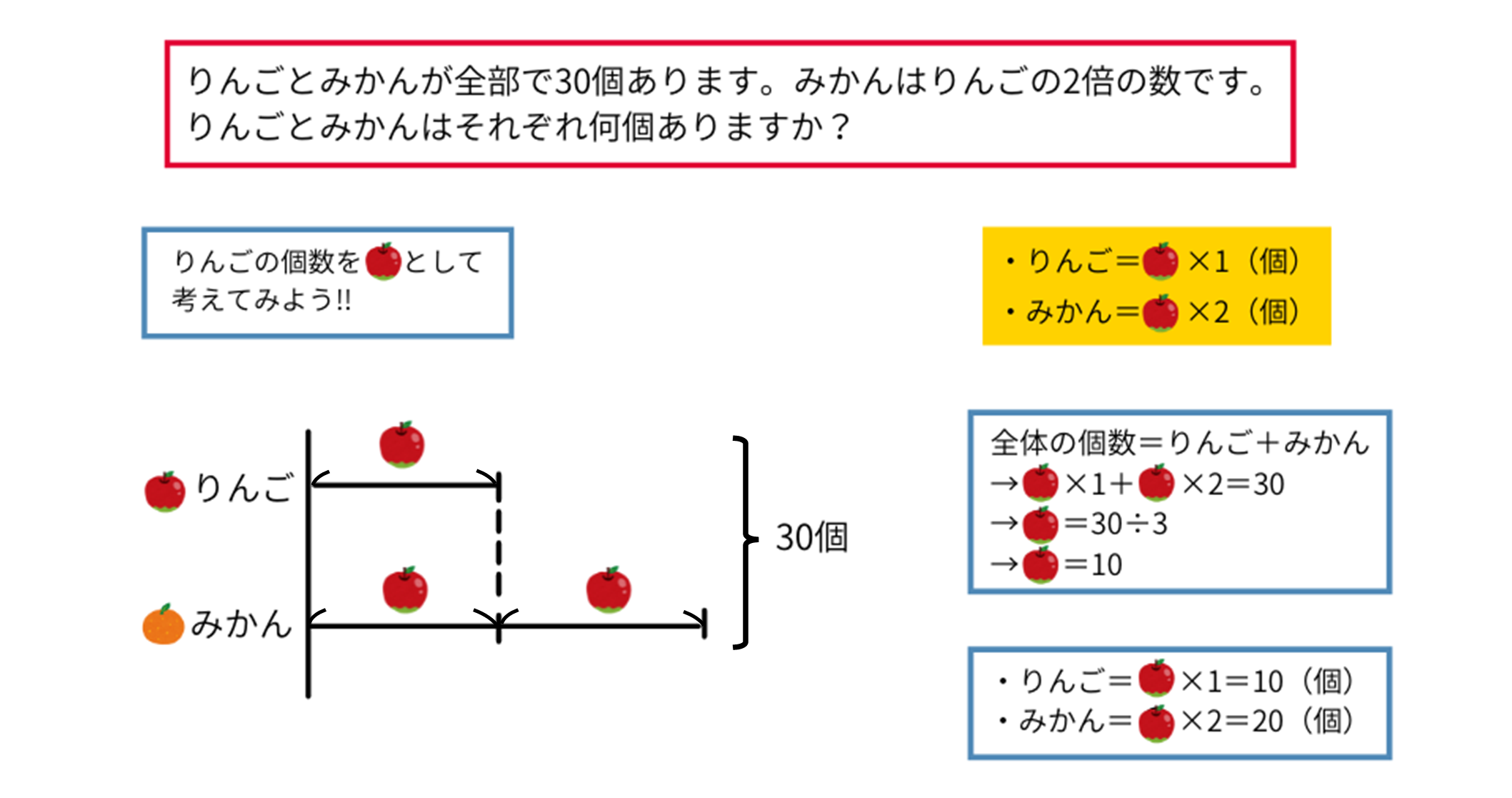
線分図を書いたら、りんごの個数を文字で置いて考えてみます。図ではわかりやすいようにりんごの絵で表していますが、こちらでは〇で表したいと思います。
りんごの個数を文字で置いたので、その文字だけで式を立てれば解くことが出来ます。（一次方程式を作ります）
りんごを〇個だとすると、みかんは（〇\(\times2\)）個になります。問題文から、りんごとみかんの合計の数は37個なので、〇（りんご）\(+\)〇\(\times2\)（みかん）\(＝30\)（個）という式が立てられます。これを解くと、〇\(\times3＝30\)で、〇\(＝10\)（個）となります。
〇はりんごの個数なので、りんごは\(10\)個、みかんは（〇\(×2\)）\(＝10\times2\)（個）なので\(20\)個だとわかります。
これを確認したところで、最初の問題を解いてみましょう。
（問題①）りんごとみかんが全部で37個あります。みかんはりんごの2倍よりも7個多いです。りんごとみかんはそれぞれ何個ありますか？
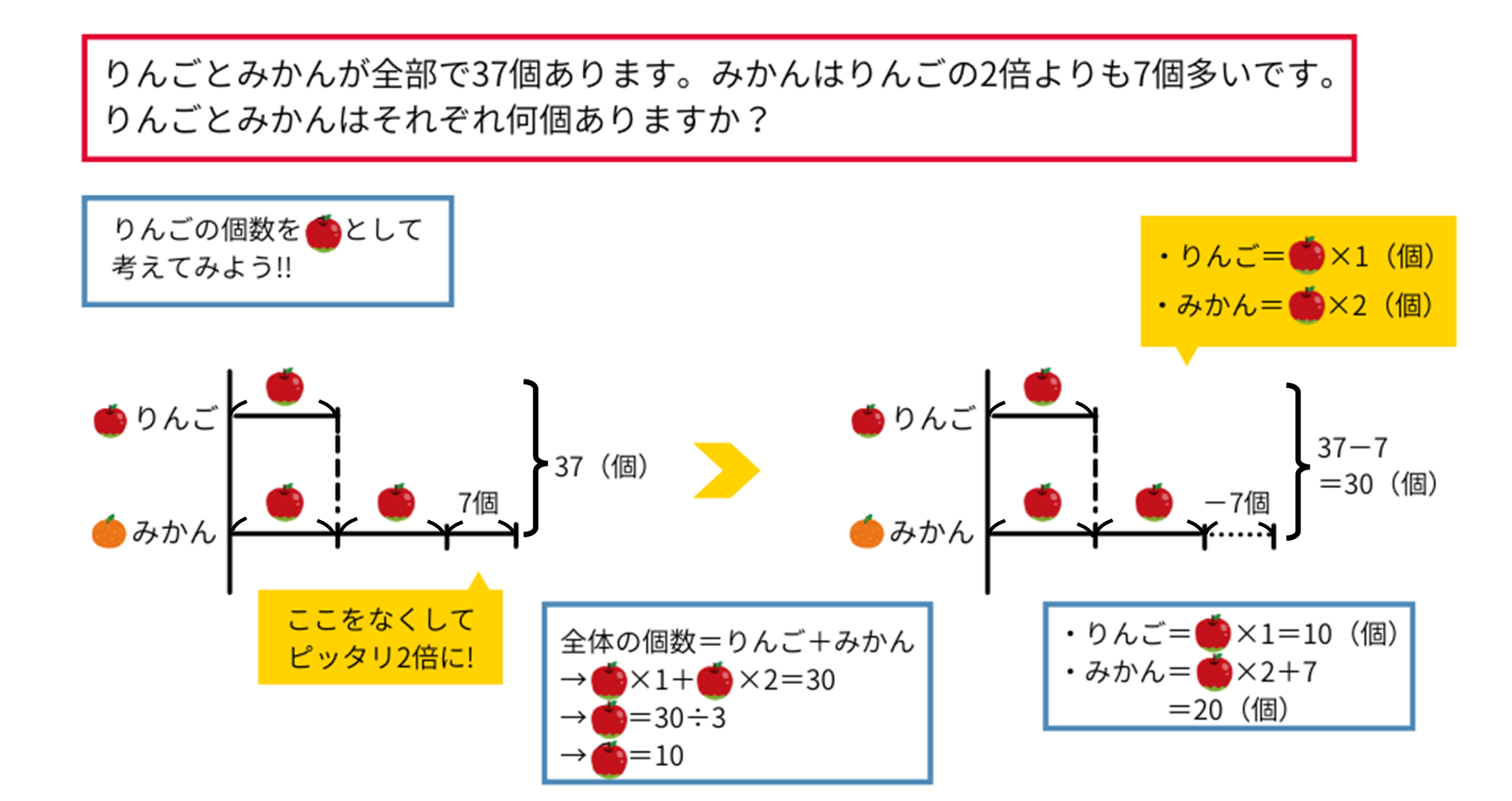
問題☆との違いは、みかんの個数がりんごの個数のちょうど2倍ではなく、2倍よりも７個だけ多い点です。これのせいで少し問題が解きにくくなってしまっています。
問題を解く側からすると、みかんの個数がりんごの個数のちょうど2倍なら解きやすいと考えるでしょう。
考え方を少し変えてみましょう。「みかんがりんごの2倍よりも７個多い」というのは、「みかんが７個少ないと、りんごのちょうど2倍になる」と考えることもできます。
そこで、みかんの個数から\(７\)個引いてみましょう。このとき、りんごとみかんの合計も\(７\)個引いて\(３０\)個になります。
すると、先ほど解いた問題☆と同じ形になります。りんごの個数を〇（図ではりんごの絵）で置いて式を立てましょう。問題☆と同じなので省略して、〇\(＝10\)（個）だと求められます。りんごはそのまま\(10\)個ですが、今回のみかんの個数は\(20\)個ではありません。
今回は解きやすいようにみかんの個数を変えているので、答えを出すときは問題文に合うように数字を戻さなくてはいけません。途中でみかんを\(-7\)個しているので、みかんの個数は〇\(\times2＋7＝27\)（個）です。
線分図での解き方（問題②）
次に、先ほどと少し違うパターンの問題を考えてみましょう。
（問題②）あめ玉が38個あります。これを太郎君と花子さんに分けると、花子さんのもらったあめ玉は太郎君のもらったあめ玉の3倍よりも2個だけすくなかった。2人は何個あめ玉をもらったでしょうか？
この問題も、まずは線分図を書いてみましょう。自分で解けそうな人はぜひ解いてみてくださいね。
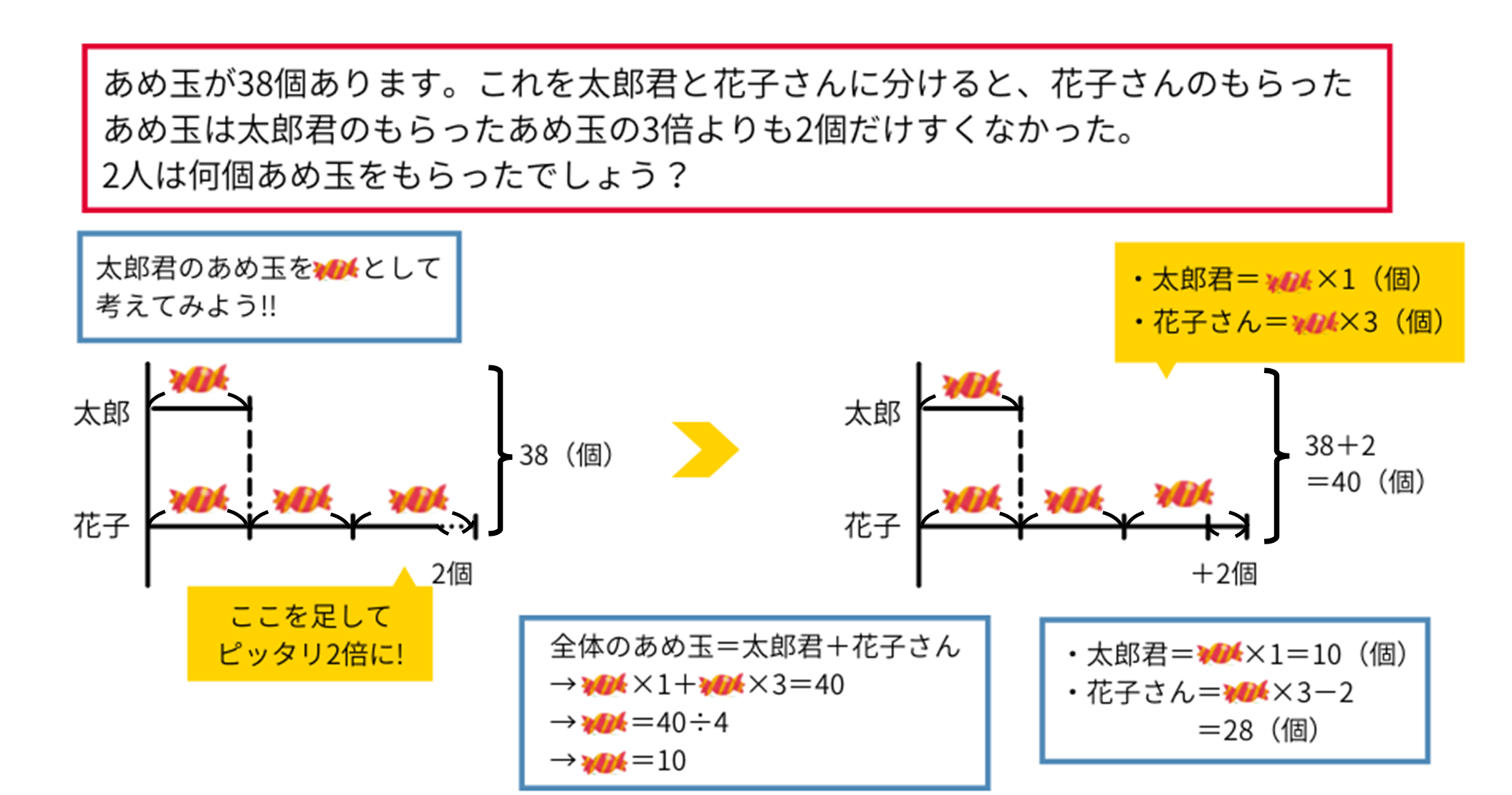
まずは先ほどと同じように数を変えて、比だけで表せるようにしましょう。
花子さんのあめ玉は太郎君のあめ玉の\(3\)倍よりも\(2\)個だけ少ないので、花子さんのあめ玉に\(2\)個足すと、ちょうど\(3\)倍になります。（図の方がわかりやすいと思います）
花子さんに\(2\)個のあめ玉を足すと、全部のあめ玉も\(2\)個増えて\(38＋2＝40\)個となります。
ここで、太郎君のあめ玉を〇個（図ではあめ玉のイラスト）としましょう。太郎君が〇個だとすると、花子さんは（〇\(\times3\)）個となります。2人の合計の個数は\(40\)個なので、〇（太郎君）\(＋\)〇\(\times3\)（花子さん）\(＝40\)（個）という式が立てられます。
これを解くと、〇\(＝10\)（個）で、太郎君のあめ玉は\(10\)個だとわかります。花子さんのあめ玉は途中で足した分を引くと〇\(\times3-2\)（個）なので、\(3\times10－2＝28\)（個）となります。
途中で足したり引いたりした場合は、最後にその数を戻すのを忘れないようにしましょう。
練習問題
これで線分図での解き方の基本は説明できたので、練習問題を解いて慣れていきましょう。
（問題③）兄のおこづかいは弟のおこづかいの2倍よりも1000円多く、兄弟のおこづかいの合計金額は5500円である。兄と弟のおこづかいはそれぞれ何円でしょうか？
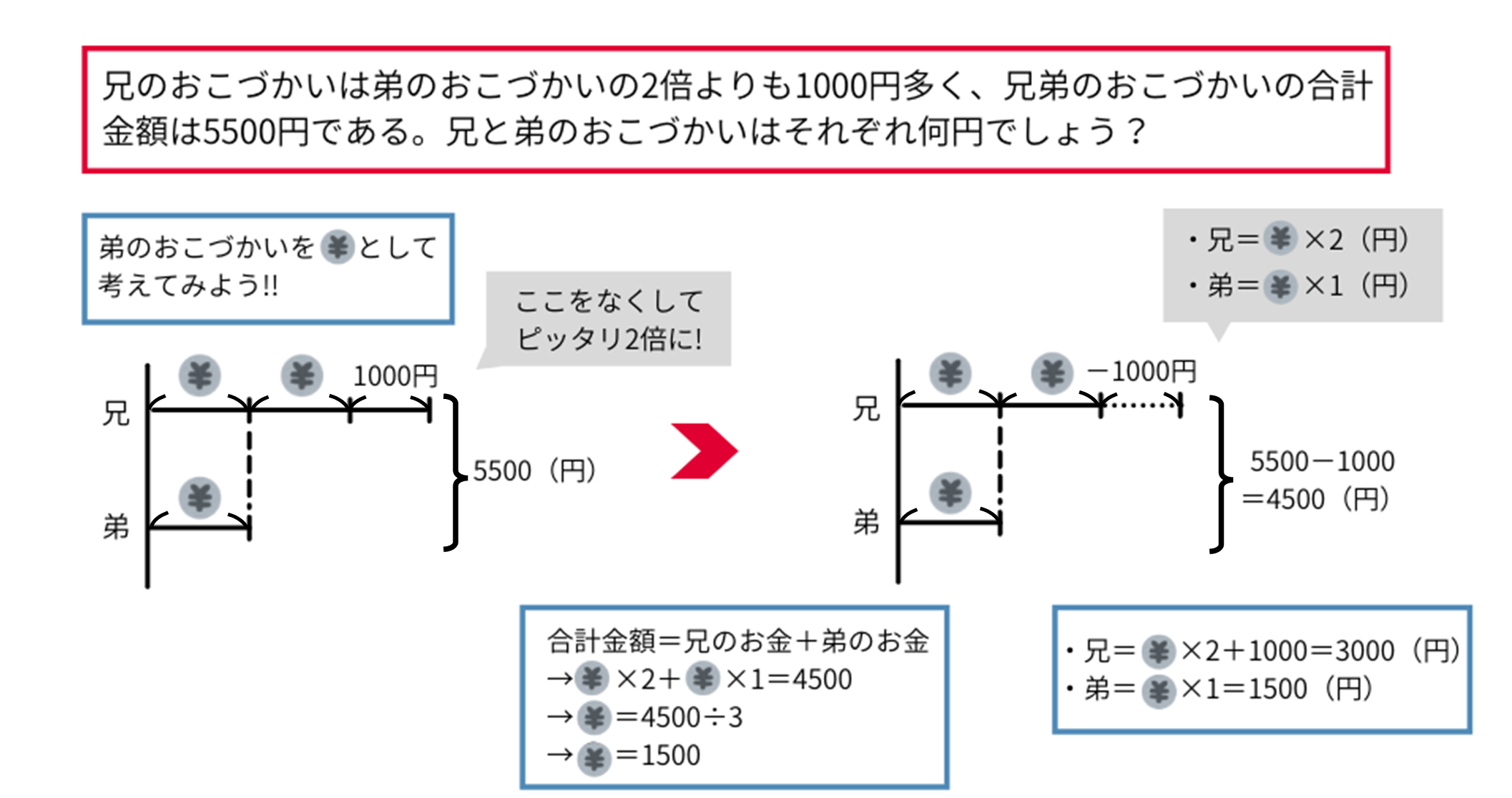
まずは今まで通り、数を足したり引いたりして比だけで表せるようにしましょう。
兄のおこづかいは、弟のおこづかいの\(2\)倍よりも\(1000\)円多いです。そのため、兄のおこづかいから\(1000\)円引けば、ちょうど\(2\)倍になるとわかります。
兄のおこづかいから\(1000\)円引くと、合計金額も\(1000\)円引いて\(4500\)円となります。
ここで弟のおこづかいを〇円（図ではお金のイラスト）としましょう。弟を〇円だとすると、兄は（〇\(\times2\)）円と表せます。合計金額は\(4500\)円なので、〇（弟）\(＋\)〇\(\times2\)（兄）\(＝4500\)（円）という式が立てられます。
これを解くと、〇\(＝1500\)で、弟のおこづかいは\(1500\)（円）だと求められます。兄のおこづかいは途中で引いた分を足すと〇\(\times2＋1000\)（円）なので、\(2\times1500＋1000＝4000\)（円）となります。
（応用）3種類の分配算
ここからは応用編として、3つのものの数を求める問題を解いていきます。数が増えても解き方は同じなので、気になる方はぜひチャレンジしてみてくださいね。
（問題）りんごとみかんとバナナが全部で80個あります。みかんはりんごの2倍より7個多く、バナナはりんごの3倍より5個少ないです。このとき、りんごとみかんとバナナはそれぞれいくつありますか？
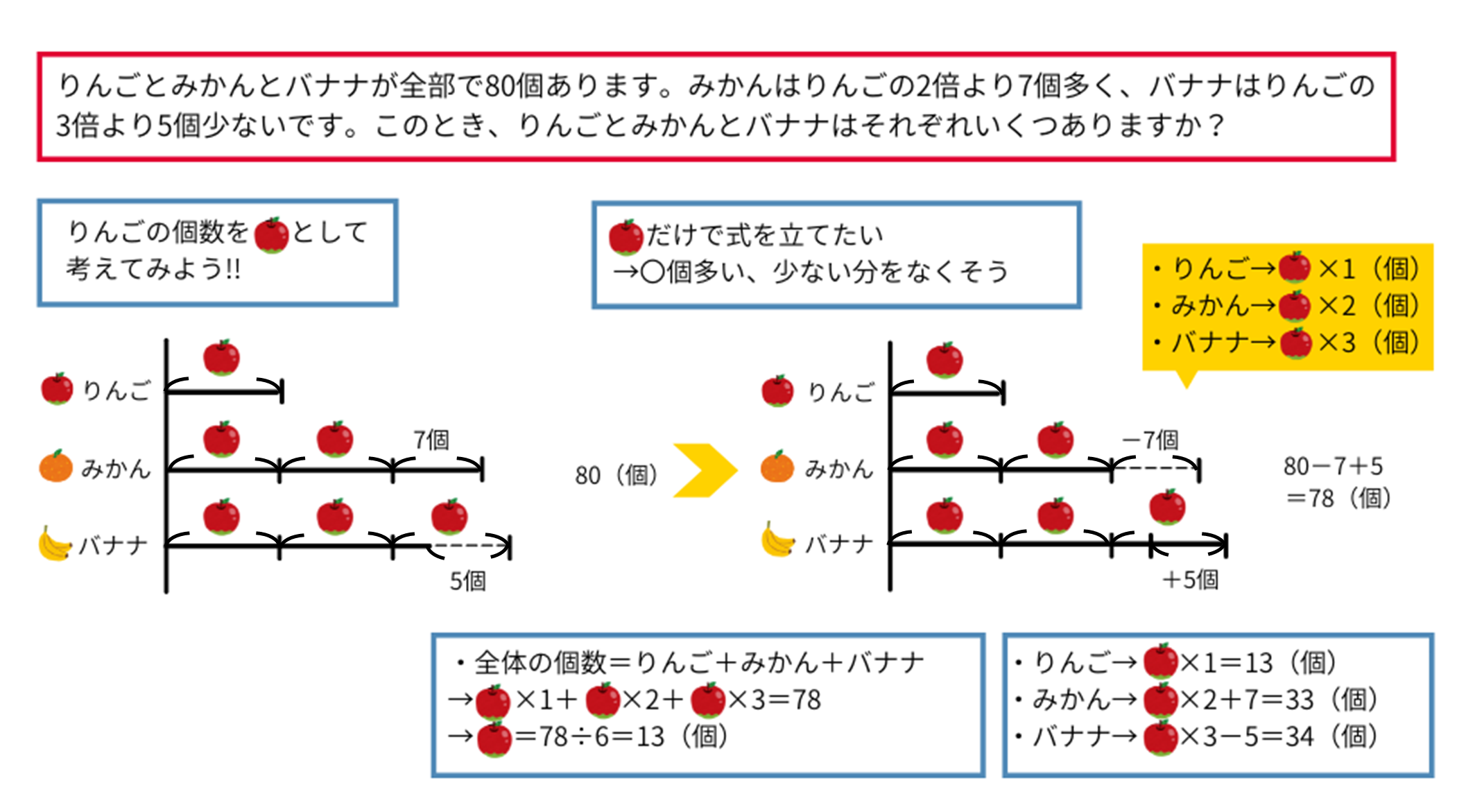
この問題も線分図を書いて考えていきましょう。3種類になっても、まずは比だけで表せるようにしていきます。
みかんはりんごの\(2\)倍より\(7\)個多いので、\(7\)個引いてちょうど\(2\)倍の数にします。バナナはりんごの\(3\)倍より\(5\)個少ないので、\(5\)個足してちょうど\(3\)倍の数にします。
このとき、合計の数は\(80－7\)（みかん）\(＋5\)（バナナ）\(＝78\)（個）になります。
ここで、りんごの個数を〇個（図ではりんごのイラスト）としましょう。
りんごの個数を文字で置いたので、その文字だけで式を立てれば解くことが出来ます（一次方程式を作ります）。
そのために、みかんから\(-7\)個、バナナに\(+5\)個します。すると、みかんが〇（りんごの個数）\(\times2\)個、バナナが〇（りんごの個数）\(\times3\)個と表せます。
全体の個数＝りんご＋みかん＋バナナ（〇\(\times1+\)〇\(\times2+\)〇\(\times3＝78\)）で、りんごの個数は\(13\)（個）だとわかります。後はこれを文字に代入しましょう。足したり引いたりした分を戻すのも忘れずに。
みかんは〇\(（13）\times2+7＝33\)（個）、バナナは〇\(（13）\times3-5＝34\)（個）です。
追加練習用プリント（無料）
練習用プリント（無料）は、
『個別指導塾テスティー』の公式LINE の友だち追加された方のみの配布となっております。
以下から公式LINEの友だち追加をして、記事の続きをお楽しみください！！
＜スマートフォンからお読みの方はこちら＞
＜パソコンからお読みの方はこちら＞
まとめ
最後に、今回使った分配算の解き方をまとめておきます。
- 与えられた情報を線分図に書く。
- 線分図を見ながら、きりのよい比にするために余分なところを引いたり、足りないところを足したりする。
- 割り算で比の値をだす。
- 求められている数値を計算する。
分配算が苦手な人も、簡単な問題や似た問題をどんどん解いて得意になってもらえたら嬉しいです。
おすすめ記事
参考
東京大学理科二類の岡部信です。
京都の高校に通っていたので東京は知らないことだらけです。特に通勤電車はすし詰め状態だと聞いていましたが、ここまでだとは思ってなかったです。実家では犬を飼っていたのですが、もう3ヶ月近く会っていないのでそれが1番寂しいです。今は千葉で父と姉と3人暮らしですが、9月からは東京で1人暮らしする予定なので楽しみです。大学ではテニスサークルと東大村塾という農業と村おこしを掛け合わせたような活動をしているサークルに入っています。趣味は料理、登山です。料理は高校の時に料理研究部に入っていたのでそこそこ出来ますが、もっと上手くなれるよう時間がある時は夕ご飯を作ったりしてます。お菓子も色々作れるようになりたいです。登山は友達と休日に日帰りで行ったり、夏休みは泊まりで行ったりもしてます。今年の夏は富士山と北海道の富良野岳に行く予定です。
皆さんよろしくお願いします。
