売買損益とは中学受験に登場する文章題の一つです。問題文を読み解くのが難しいという性質上,学校や学習塾でも頻繁に対策が行われる分野なのですが,なかなかコツが掴めず苦戦してしまう人が多いです。そこで本記事では,売買損益についてご紹介するシリーズの応用編として,受験問題を引用しながら攻略法をご紹介していきます。よろしければ一読してください。
Contents
基礎編の振り返り!重要なポイント3つを思い出そう!
それでは問題演習へと移りたいところですが,まずは前回の基礎編で確認したことをおさらいしていきましょう。そもそも売買損益とはモノの売り買いについての文章題のことを指しました。計算自体はそこまでややこしくないものの,用語の難しさだったり整理のしにくさだったりという難点から,点が取りにくい範囲の一つだと言えるでしょう。
そこで前回の記事では,回答を導くうえでいくつか重要なポイントをお教えしましたね。まず一つ目が用語の確認です。売買損益には,定価・原価・利益といった耳馴染みのない単語がたくさん登場します。それらの意味をひとつひとつ丁寧に紐解いていき,問題文で描かれているシチュエーションを正確に想像することが大切になってきます。
二つ目のポイントが整理した問題の中身を線分図に書くというものでした。このとき重要なことが原価・定価・売価の3つの線分で価格や割合を比較していくことです。線分図を使うというテクニックは色々な問題で登場するモノですが,問題文によって書き方を変えるというのが受験においては大切になってきます。売買損益では価格の変化への注目が攻略へのカギとなってきますので,いくつかの価格が一度に比較できるようまとめてあげることがいいでしょう。
三つ目のポイントとしては,〇〇割増し・〇〇割引きの計算を間違えないようにしようということをご紹介しました。売買損益では「原価の〇○割増しを△△割引きして,更にそこから□□割増しすると……」といった文章がよく見かけられます。このような文章が出てきたときに,しばしば足し算や引き算で最終的に何割変化したのかを求めようとしてしまう人がいますが,それでは正しい回答が求められません。割増・割引の関係はかけ算・割り算で計算するものですので,その点を意識しながら解いていくといいでしょう。
以上が重要なポイントの復習でした。まとめると次の図のようになります。もし思い出せない人やいまいちピンとこない人がいましたら,前回の基礎編の記事を改めて読んでみてください。
演習① 基礎を確認しよう!
ではここからは本題の問題演習に移りましょう。まずは基礎編の振り返りの章で確認した事項をおさらいするという目的で,やや簡単めな問題を引用しました。計算ミスなどに気をつけながら,ウォーミングアップがてらに解いてみてください。
次の□に当てはまる数を求めなさい。
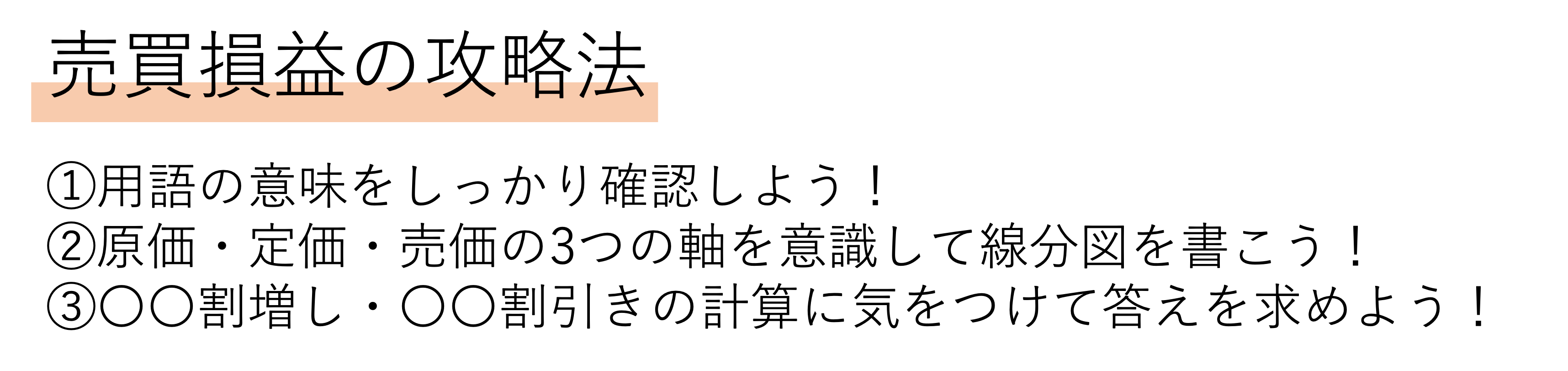
ある品物の定価は原価の2割増しの3000円でした。この品物の価格は□円です。
(富士見中学校(2017),一部改題)
解説①
いかがでしたしょうか。今回の問題は文章が短めで,その分考える要素も少なかったためときやすく感じた人もいるでしょうが,用語や線分図への理解が十分でないと正しい答えにたどり着けなかったかもしれません。基礎編で確認したステップをなぞりながら,一緒に答えを確認していきましょう。
まずは問題文の整理からですね。といっても今回は定価と原価という言葉しか出てこなかったので確認する必要はないかもしれませんが,一問目ということで丁寧に進めていきましょう。定価とはモノが売られている通常の金額を,原価とはモノを買ったときに支払われた金額のことを指しました。そしてこれらのことを線分図に整理すると次のようになります。ここで線分図に情報を起こすときに気をつけておきたいことが,線の長さと数値を揃えようとすることですね。当たり前のように聞こえますが,線の長さと数値が揃った線分図は後から見返しても分かりやすいですし,計算ミスも起こりにくいです。その点に注意して線分図を書いてみると更に簡単に問題を解くことができるでしょう。
さてこのように線分図が整理できたところで,後は計算式さえ作ることができれば問題の答えが導けそうですね。ここで思い出して欲しいのが〇〇割増し・〇〇割引きの解き方です。2割増しで3000円ということは,定価は原価の12割になっています。このことに注目すると,原価と定価に関して次のような関係が成立することが分かります。
定価=\(原価×\frac{12}{10}\)
あとは定価が3000円であることや分数のかけ算の計算方法を活かしながら,この計算を解いていきましょう。
定価=\(原価×\frac{12}{10}\)
原価=3000×\(\frac{10}{12}\)
原価=2500
したがって答えは2500円になります。解いてみると意外と簡単かもしれませんでしたが,用語の整理の仕方や線分図の書き方などで意外と落とし穴も多い問題でした。2割増しの部分を勘違いして分子と分母を逆にしちゃったりするだけで正しい答えにたどりつけなくなります。簡単な問題ほど注意して解き進めていくといいでしょう。
A.2500円
演習② 利益を交えた計算に慣れよう!
次の問題では少し問題のレベルがアップします。少々解きにくくなったり計算が長くなったりするでしょうが,基本的なポイントは変わりません。基礎に忠実に進めていきましょう。
次の□に当てはまる数を答えなさい。
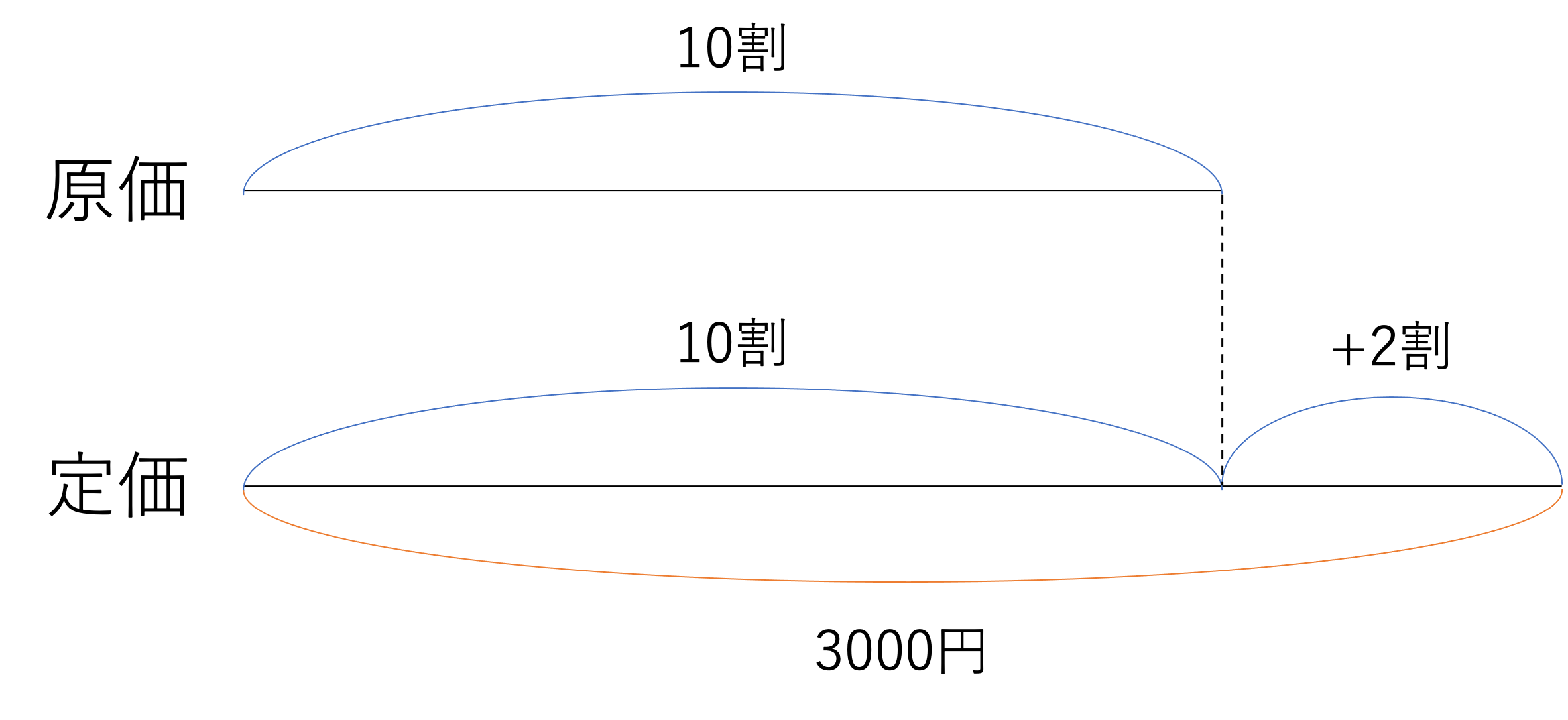
仕入れ値□円の品物に4割増しの定価をつけたところ,売れなかったので,その定価の2割引きで売ったところ,60円の利益がありました。
(法政大学中学校(2016),一部改題)
解説②
それでは解説に移ります。2問目ということで先程の問題よりは簡潔に解説していきますが,1問目に無かった要素が登場していたりするので,その辺りの説明はもちろん怠らずに答えの求め方をご紹介いたします。
まずは用語の確認です。今回は仕入れ値・定価・売価・利益という4つの語句が登場していました。このうち仕入れ値は原価のことを指すので,売価と利益についてだけ軽く触れておきましょう。売価とは定価を変更して売ったときの金額になります。定価の変更にはいくつかの理由が考えられますが,主な理由が売れなかったことによる値下げです。今回も値下げによって2割引きになっています。定価と区別がつくように覚えておきましょう。次に利益についてですが,こちらはお店の儲けのことを指し,売価もしくは定価から原価を引くことで計算できます。今回は60円の利益があったとのことなので,原価と売価との差が60円だということが分かりますね。
このように用語の中身を詳しく調べたり思い出したりしていくうちに,情報が頭の中でなんとなく整理できたことでしょう。そこで次は線分図の作成に移ります。主な書き方は1問目と同じですが,この問題では売価も合わせて3本の線分に情報を書き出さなければいけません。その点に注意して図を書くと,下のような線分図が出来上がります。
それでは線分図が書けたところで次のステップに移りましょう。次は売価や定価を原価で表す,という作業に移りましょう。このような計算をする理由は数値と割合との関係にあります。売買損益で重要なことは割合と数値とを照らし合わせて答えを考えることになのですが,今回登場している数値は60円という利益の部分しかありません。そこで60円という利益が原価の何割・何%だと言えるのかを考えないといけないのですが,その計算のために売価や定価を原価で表すというわけですね。順番に関係を考えると,次の2つの式が成立します。
定価=\(原価×\frac{14}{10}\)
売価=\(定価×\frac{8}{10}\)
そして2つの式のうち,下の売価に関する式の定価の部分に上の式を当てはめると,売価が原価の何倍かを示すことができそうです。当てはめていくと次のような式にまとめられます。
売価=\(原価×\frac{14}{10}×\frac{8}{10}=原価×\frac{112}{100}\)
このことから売価は原価の12%増しの値段だということが分かります。つまり,ここで売られているモノの売価には原価の12%が利益として加算されているということです。さて,ここで問題文に戻って利益の額を確認するとその金額は60円でした。したがって原価の12%=60円という関係が導けるのです。そして今回求めなければならないのは原価・仕入れ値の価格だったので,比の関係から計算をしていくと答えは500円となります。
12%:60円=100%:仕入れ値
1%:5円=100%:仕入れ値
仕入れ値=5×100=500円
A.500円
今回の問題では利益・売価という用語が登場しましたが,基本売買損益の問題には利益が絡んでくると思っておくといいでしょう。中には1問目のような原価と定価の関係だけが提示される問題もありますが,原価・定価・売価という3つの価格の関係には慣れておきたいところです。
演習③ 求められているものに注意して計算しよう!
利益に関する計算を進めてみたところで,次は求めるべき答えがやや分かりづらい問題にもチャレンジしてみましょう。といっても基本的な解き方は変わりません。丁寧に線分図を書くことを意識して計算していきましょう。
次の□の中に適する数を入れなさい。
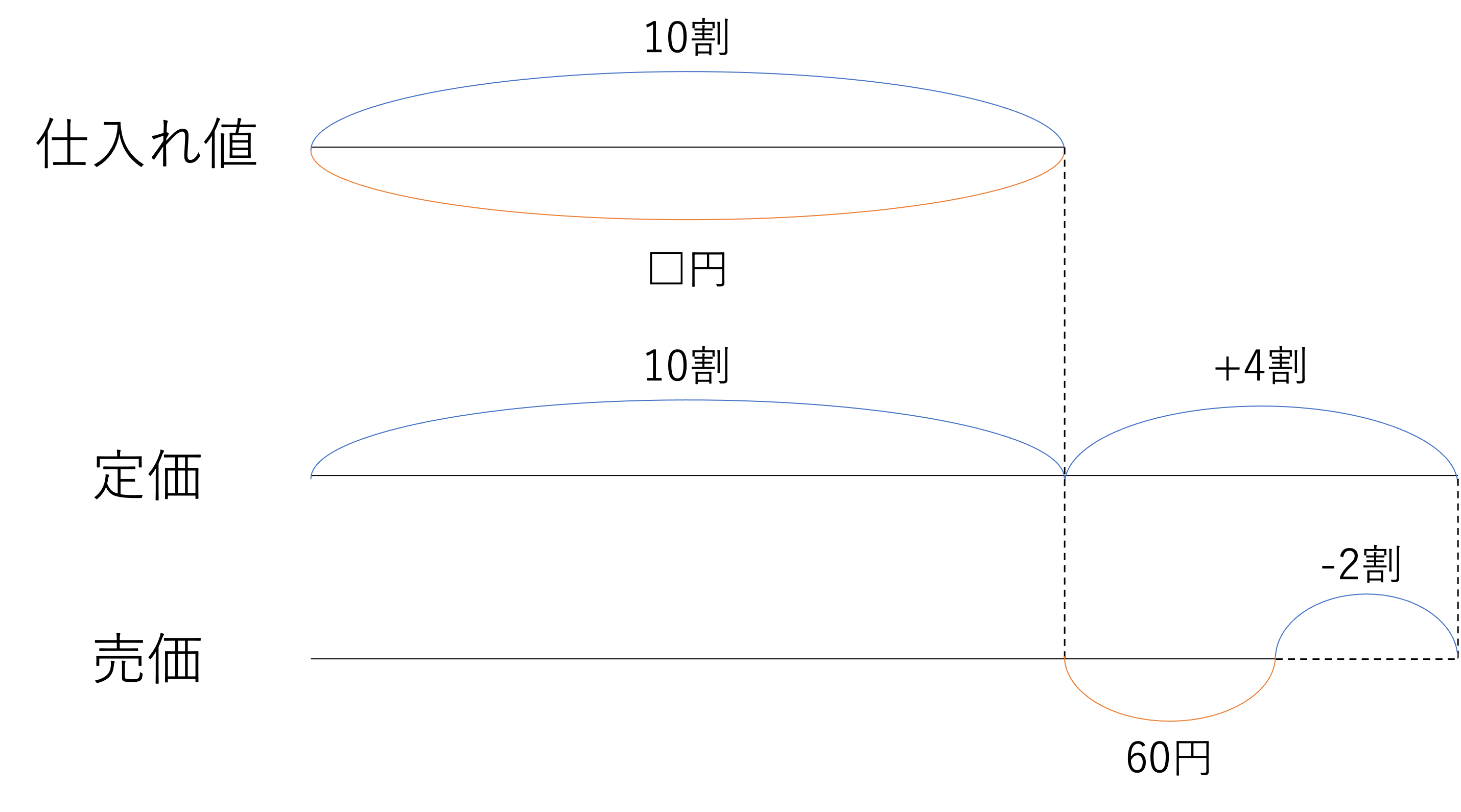
仕入れ値200円の品物に□%の利益を見込んで定価をつけたところ売れませんでした。そこで,定価の2割引で売ったところ,仕入れ値より40円高く売れました。
(法政大学第二中学校(2015),一部改題)
解説③
さてここからは解説に移りましょう。用語については1問目と2問目で解説したので今回は省略してしまいます。この問題でも仕入れ値・定価・売価という3つの価格が登場しているので,それらを比較できるような線分図を作ることを目標に,問題を読み進めていきましょう。今回の問題で重要なポイントは利益率,つまり原価の何%が上乗せされて売られているかという要素が□%であることです。この部分を求めなければいけないという点でやや要領が変わってきますが,解き方や書き方に違いはありません。□%という部分に気をつけて図を書くと次のようになります。
このような線分図が書けたところで,次は計算式を組み立てましょう。これまでの2つの問題では原価を基準に低下や売価を表すというアプローチで攻略を進めていきましたが,今回もこの手法が使えます。実は売買損益のほとんどの問題は,定価や売価を原価で表すことで答えを導くことができるのです。もちろんそうでない問題や別の方法を使った方がいい場合もありますが,大体は原価を中心に考えていけばいいと理解しておくと本番の受験でも役に立つでしょう。
定価=\(仕入れ値×\frac{10+□}{10}\)
売価=\(定価×\frac{8}{10}\)
さて,このような2つの式が完成したところで次は1つの式にまとめるという作業に移行しましょう。この作業も既に2回行っているので説明は特に必要ないでしょう。また今回の問題では仕入れ値が200円だったという説明もあったので,その点も交えて式に起こすと以下のような関係が成立します。
売価=\(仕入れ値×\frac{10+□}{10}×\frac{8}{10}=200×\frac{(8×(10+□})}{100}=200×\frac{(80+8×□})}{100}\)
ここで元の原価が100%であることを考えると,少々難解ですが,売価は原価の(80+8×□)-100=8×□-20%増しの値段になっていることが分かります。ここで,問題文で「仕入れ値より40円高く売れました」と書いてあることを思い出しましょう。つまり利益が40円発生しているというわけですね。したがって,原価の(8×□-20)%=40円という関係が成立します。これだとまだ難しいので,40円という利益が200円という原価の20%に相当することを考えると,次の関係が成り立つと判断できます。
(8×□-20)%$=20%
8×□$=40
□$=5
このことから□の中身は5となるため,単位に気をつけ形を整えると,答えは5%となります。
A.5%
□をきちんと使った売買損益の計算は基礎編・応用編通して初めて引用しましたが,無事解けたでしょうか。おそらく苦戦した人もいることでしょう。しかし冒頭でも述べた通り,ベースとなる解き方は変わりません。たくさん演習を積んで慣れていきましょう。
演習④ 設定が複雑な計算に挑もう!
最後に挑戦していくのは設定が複雑な問題です。問題文を見ていただければ分かる通り,文章がとても長く,読解に時間がかかりそうですね。ゆっくりでもいいので,正確に情報を整理して正しい答えを導けるように頑張っていきましょう。
原価 80円の品物をいくつか仕入れ,原価の4割の利益を見込んで定価をつけました。しかし,販売前に仕入れた個数のうち何%かが不良品であったことに気づき,その不良品を返品して,そのぶんの代金も返してもらえました。そこで,原価の5割の利益を見込んだ定価に変更して販売したところ,予定していた利益と同額の利益を得ることができました。仕入れたもののうち不良品だったものは何%ありましたか。
(八雲学園中学校(2013),一部改題)
解説④
それでは4問目の解説に移りましょう。まずは問題文を整理していきます。この問題では原価・定価・売価という3つの要素が登場していますが,それだけではなくモノの個数まで考えなければいけません。ただ以上の3つの要素に基づいて線分図を書いていく,という手順に変わりはありません。条件をまとめていくと下のような図が出来上がるはずです。
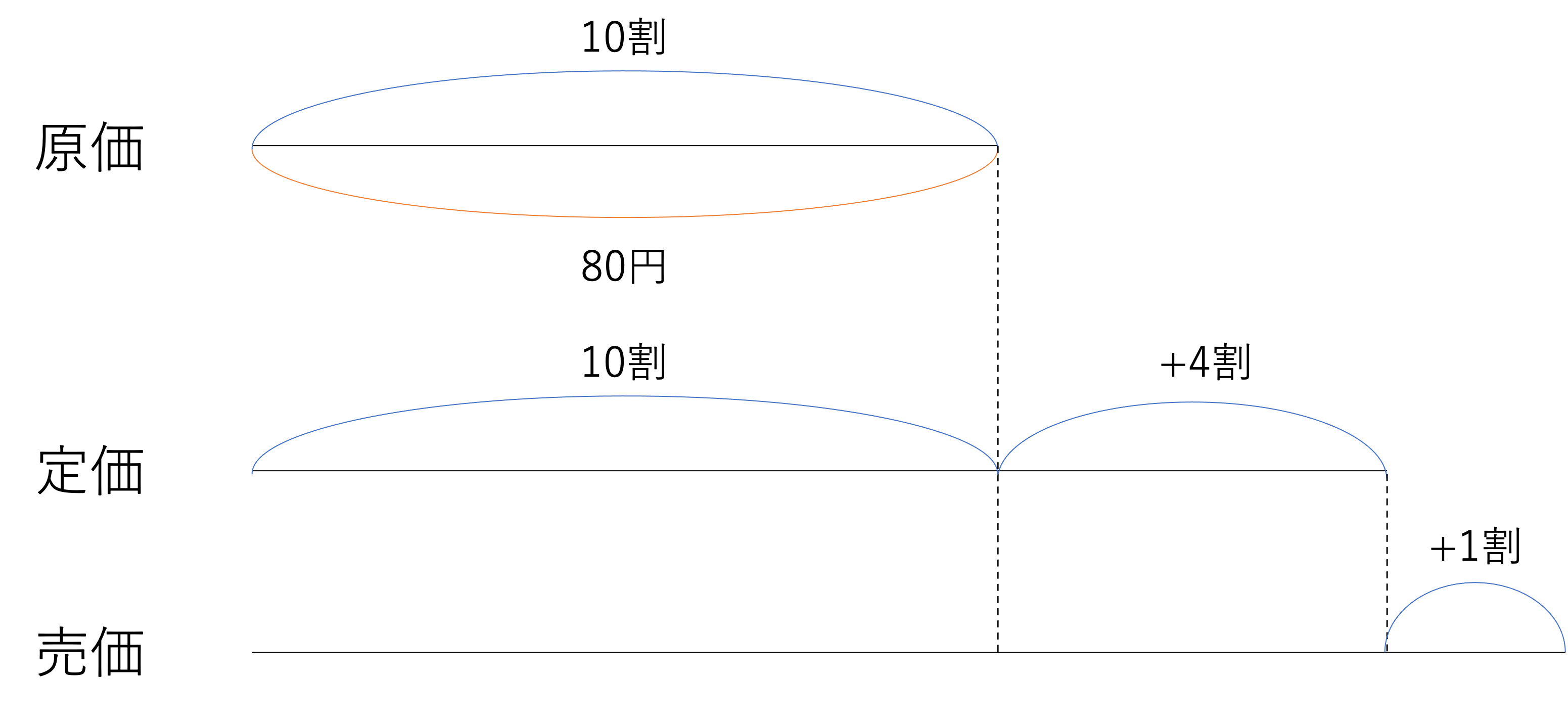
まずはこの図に基づいて,一度個数のことは考えず,モノの金額について整理していきましょう。問題文では,原価が80円で定価は4割の利益が出るようにつけられたと述べられていました。このことから定価は次のようになるはずです。
定価=原価×\(\frac{14}{10}=80×\frac{14}{10}=112\)
また売価,つまり一度つけた定価を変更したときの値段に関しても,原価の5割の利益を見込んだ額と言われているので,次のような計算から売価は120円になると分かります。
売価=原価×\(\frac{15}{10}=80×\frac{15}{10}=120\)

さて,ここからは利益という観点から個数との関係について見ていきましょう。今回は2パターンの利益が登場していました。その1つが予定されていた利益です。いま作った数を○個とすると,この利益は定価×個数=112×○円ということになります。そしてもう1つの利益とは,不良品が出てしまったときの利益です。こちらの金額は売価×個数で計算することができます。不良品が全体の□%出たとすると,120円で売ったモノの個数は全体の100-□%になるわけですから,このときの利益は120×○×\(\frac{100-□}{100}\)円となりますね。ここで,見落としてはいけないのが不良品の行方です。
問題文より発生してしまった□%の不良品は「返品して,そのぶんの代金も返してもらえました」と言われています。つまり返金されてきた分の金額を計算しなければ正確な答えは出せないということですね。では返金がいくら発生したかと言うと,原価が80円・不良品が全体である○個のうち□%であることから,80×○×\(\frac{□}{100}\)円となります。
そして「予定していた利益と同額の利益」が得られたと言われているので,予定されていた利益=不良品が出てしまったときの利益+返金,という関係が導けます。その理由は個数の一致です。よくある間違いが返金を考えていない式で計算を進めてしまうというものですが,返品した不良品と売った正規品を合計しないと○個にならないので,この2つを足さないと個数がずれてしまいます。作ったモノの全体の行方を追うことを意識して計算式を作りましょう。以上の説明から次の式が成り立つことが分かります。
\(112×○=120×○×\frac{100-□}{100}+80×○×\frac{□}{100}\)
いまこの式において,左右で○という値が共通していますね。他にもカッコを外したり分母を払ったりして,式をより簡単にすることができそうです。少しずつ計算を進めていくと,次のように□の中身が求められ,その結果不良品は全体の20%になるという答えが求められます。
\(112=120×\frac{100-□}{100}+80×\frac{□}{100}\)
11200=120×(100-□})+80×□
11200=12000-120×□+80×□
40×□=800
□=20
A.20%
この問題は結構難易度が高めであり,不良品や返金といった要素まで絡んでくる問題はそうそう登場しません。しかし万が一登場しても答えを導けるように,たくさんの問題に挑戦しておくといいでしょう。
まとめ
今回は売買損益に関する計算の解き方の応用編ということで,厳選した4つの受験問題を引用しながら攻略法についてご紹介していきました。どんな問題でも基本は線分図を作って原価との関係を見ていけば答えを求めることができます。その点だけでも頭に入れていただけますと幸いです。よろしければおすすめ記事や参考書籍も使いながら得点力アップにつなげていきましょう。

















