今回は消去算の応用についての記事となっております。消去算とは何か,という基礎的な知識から取り扱い,実際に入試で登場した問題を引用しながら攻略法をご紹介していきます。
Contents
消去算とは?
初めに消去算とは一体どんな問題を指すのか,について確認していきましょう。この問題は算数の文章題の中で,「ある2つのものの数が登場する計算で,片方を消去することで答えが導ける」というものになります。2つのものの数とは?消去するとは?と疑問に思われる方もいるかもしれません。そこで,一つ例題を見ていくことにしましょう。
ぶどうを1個,みかんを3個買うと460円になります。また,ぶどうを2個,みかんを5個買うと800円になります。ぶどうとみかんはそれぞれ何円でしょう。

このような問題が消去算です。ぶどうとみかんという2つのものの数が出てきていることがわかりますね。片方を消去するとは,この2つの数についての情報を1つに減らすことを指します。ぶどうだけ・みかんだけ,のどちらかで値段を表すという意味ですね。
この消去算は,小学校や塾で詳しく学習するものではありません。難しい図形の問題の方が取り上げられがちです。しかしこのような文章題は受験の基礎なので,早いうちからの対策が望ましいです。
ただ,これまで消去算を知らなかったとしても,この記事を読んで完璧に対策できれば問題ありません。一緒に消去算の解き方を学習していきましょう。
基本的な解き方
それではまず基本的な解き方について学んでいきましょう。解く手順はたったの2ステップです。上で取り上げた例題を使いながら,それぞれのステップを抑えていきましょう。
ぶどうを1個,みかんを3個買うと460円になります。また,ぶどうを2個,みかんを5個買うと800円になります。ぶどうとみかんはそれぞれ何円でしょう。
ステップ1:片方のものの数を揃える
まず大事なことが,片方を消去するためにどちらか一方のものの数を揃えます。今回はぶどうについては1個の場合と2個の場合が,みかんについては3個の場合と5個の場合が登場しています。したがってぶどうの方が数を揃えやすいですよね。2個でぶどうの数を揃えて計算を進めましょう。
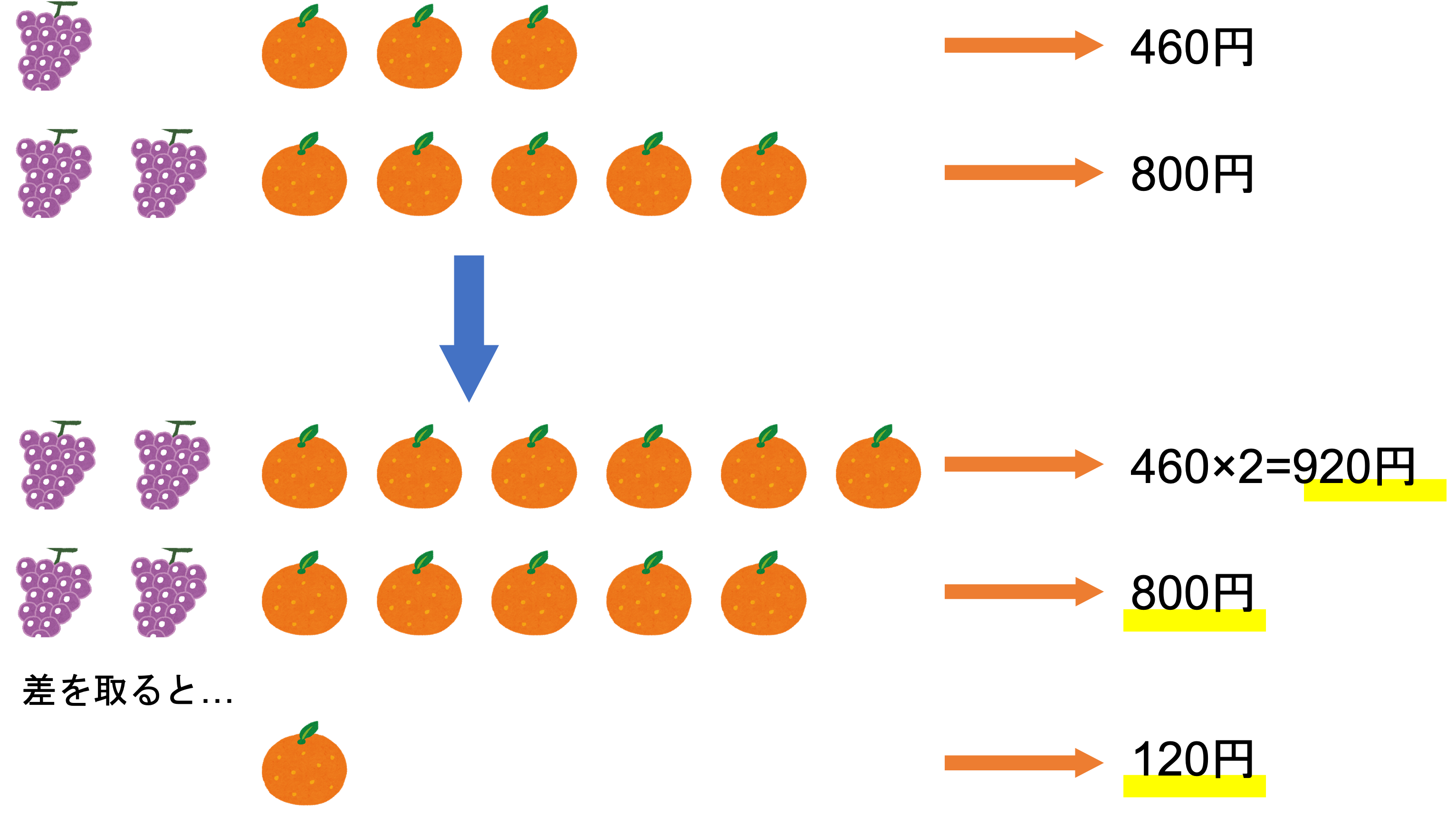
ここで数を揃えるというのは,ものの数の最小公倍数を見つけてぶどう・みかん・値段の値を何倍かして合わせる,ということを指します。例えば今回は次のように操作すれば数が揃えられます。

今回は「ぶどう1個・みかん3個」で460円という関係をすべて2倍すると,ぶどうの数が2個で揃えられますね。この上と下とを比較すると,みかんが1つ増えると値段が120円高くなるという関係がわかります。このように片方を揃えて差を求める,つまり消去すると一方の価格が求まります。
今回はみかん1つで120円増える,つまりみかんは120円とわかりました。ただこれはみかんが2個でも3個でも問題ありません。その場合,全部合わせたときの金額をものの個数で割ればいいので,柔軟に対応しましょう。
ステップ2:求めた答えを当てはめる
ステップ1より片方の数を揃えて消去した結果,みかんが1つ120円だと導けました。次のステップではこの結果を使ってぶどうの値段を求めていきましょう。
みかんが1個120円ですから,3倍すると3個で360円になります。ここでぶどう1個とみかん3個で460円という条件を思い出しましょう。このことからぶどうが1個加わると100円増える,とわかります。

このことからぶどうの値段は100円だと求められました。以上のことからぶどうは100円・みかんは120円とわかります。
A.ぶどう100円,みかん120円
以上のように,片方のものの数を揃えて消去する→求めた値を活用してもう片方の値段を計算する,という手順を踏むと消去算を解くことができます。数を消去する,という作業にさえ慣れしまえば比較的解きやすいので,以下で引用する問題を解きながら手順を身につけていきましょう。
問題① 基本的な消去算
それではここからは実際に入試に出題された問題を解きながら,消去算の攻略法を覚えていきましょう。最初は先程の例題に類似した問題ですので,解きやすいかと思われます。
アイスクリーム3個とかき氷9杯の代金は660円で,アイスクリーム9個とかき氷10杯の値段は1130円でした。アイスクリーム1個は何円ですか。
(かえつ有明中学校(2016),一部改題)
解説①
ではここからは解説に移ります。消去算で必要なステップは,数を揃えて消去する・求めた答えを使って計算を進める,ということでしたね。そのためこの手順に沿って問題を解説していきます。
まず,この問題ではアイスクリームとかき氷の2つのものが登場していました。上はアイスが3個・かき氷が9杯,下はアイス9個・かき氷10杯となります。したがってまずは,アイスクリームで数を揃えるのか,それともかき氷で数を揃えるのかを考えましょう。
アイスクリームで揃えた場合,3(個)と9(個)の最小公倍数は9であることから9個で揃えて消去すればよく,かき氷で揃えた場合,9(杯)と10(杯)の最小公倍数は90であることから90で揃えて消去すればいいとわかります。この場合,アイスクリームの方が揃えやすいことがわかりますので,アイスを消去するように計算していきましょう。
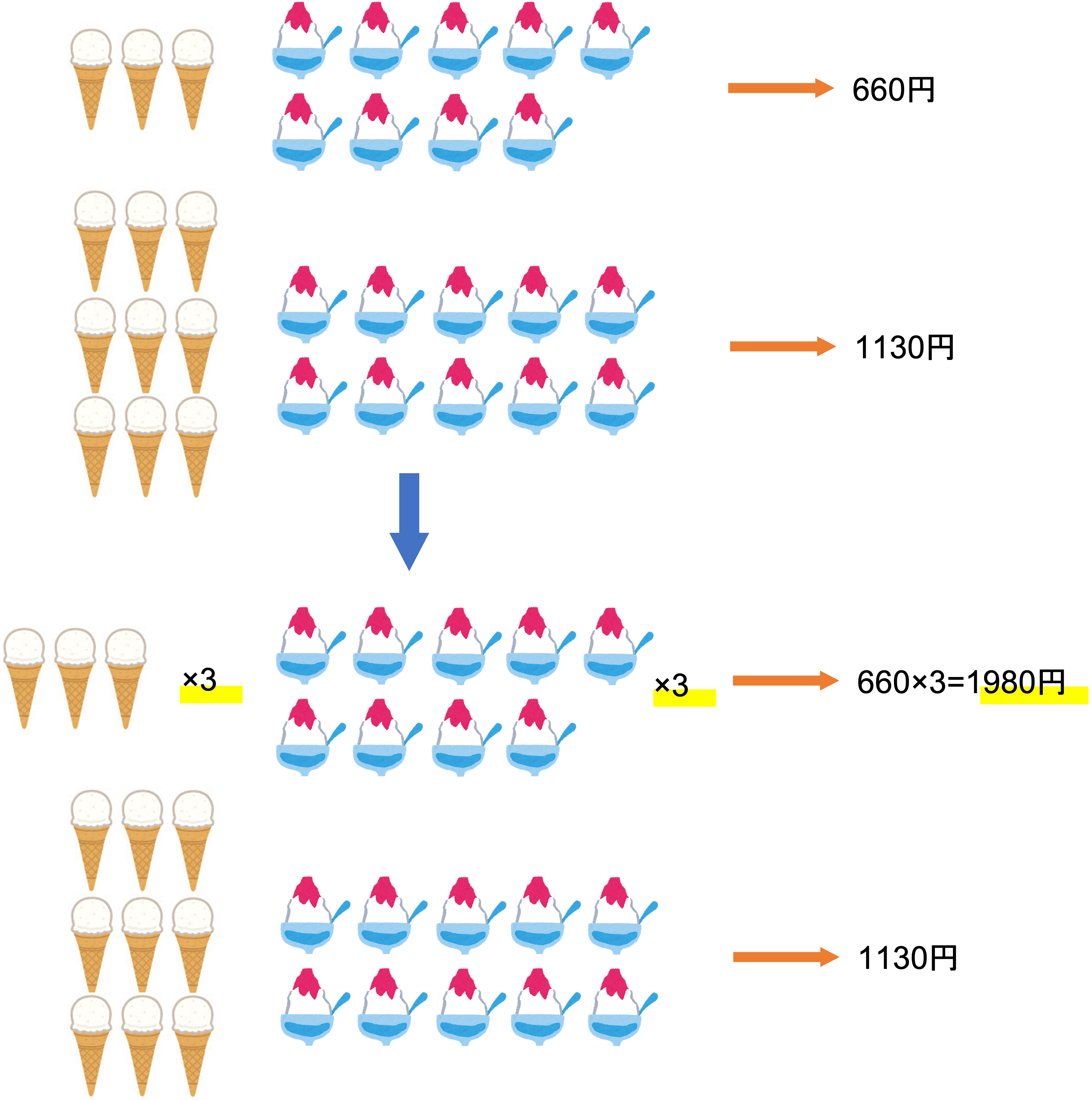
したがって上の図のように,アイス3個・かき氷9杯の条件を3倍すると,アイスクリーム9個・かき氷27杯で1980円という新たな条件を導けました。
よってこれらの差を取ると,かき氷が17杯増えると850円高くなるという関係が求められます。そして値段をかき氷の数で割ると,かき氷が1杯増えると50円高くなる。すなわちかき氷は1杯50円だと計算できました。
ではこの値を使ってアイスクリームの値段も求めましょう。かき氷が1杯で50円ということは9個で450円です。ここでアイスクリーム3個とかき氷9杯の代金は660円であったことから,かき氷9杯の値段を差し引くと,アイスクリーム3個で210円だとわかります。
このことから,値段を3で割ると70となるので,アイスクリームの値段は70円だと求められました。
A.アイスクリームは1個70円
このように揃える・消去するという手順を踏めば簡単に消去算を解くことができます。計算ミスだけ気をつけて,取り組んでいきましょう。
問題② 割合が関連する消去算
それでは2問目に移ります。今度は少し難しい問題に挑戦してみましょう。この問題には割合の要素が絡んできますので,その点に注意して解いてみましょう。
ある店では,果物を合わせて10個以上買うと1割引きになります。この店では,みかん5個とりんご4個を買うと880円です。また,みかん10個とりんご5個を買うと1260円です。1個の値段は,みかんとりんごそれぞれいくらですか。
(獨協中学校(2017),一部改題)
解説②
それでは2問目の解説に移ります。今回大切なのは,まず消去する前に割引される前の値段を求めなければいけないということです。
みかん5個・りんご4個のとき,合計が10個を超えません。しかしみかん10個・りんご5個のとき,合計が10個を超えることから,1260円というのは1割引した後の値段になります。
このことから,まずはみかん10個とりんご5個を買ったときの割引前の値段を考えましょう。そのために割引した後の値段がどのように計算されるか,について考えていきます。今回は1割引き,つまり9割の値段になるので,割引後の値段は次のように計算されます。
割引前の値段\(\times0.9\)=割引後の値段\(\ =1260\)
このことから,1260を0.9で割った値が割引前のみかん10個・りんご5個の値段の割り引い前の値段になるとわかります。この計算を行うと次のようになるため,割引前の値段は1400円となります。
\(1260\div0.9=1400\)
ここまでの計算から,みかん5個・りんご4個を買うと880円になる,みかん10個・りんご5個を買うと1400円になると問題の内容を整理できました。あとは通常の消去算の要領で解いていくだけですね。
ではまずは片方のものの数を揃えて消去するところからです。今回はみかんの方が揃えやすそうなので,みかんを消去していきます。
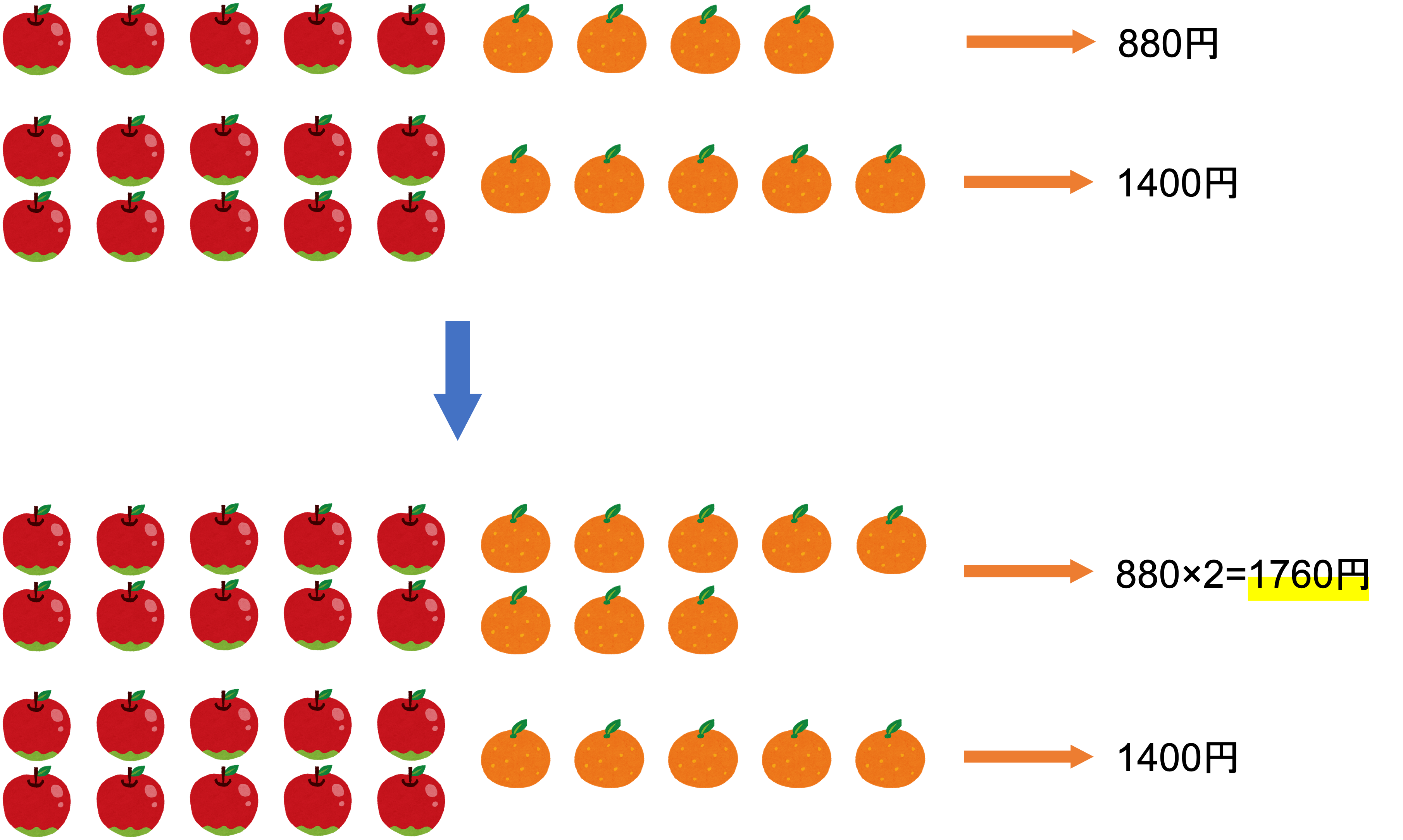
この図から,みかんが3個増えると360円値段が高くなるという関係が導かれました。したがって360円という値段を3個という数で割ると,みかんは1個120円だとわかります。ここでみかんの値段が明らかになったので,もう片方のものの値段,すなわちりんごの値段を求めていきましょう。
みかんが1個120円だということは,4個で480円になります。ここで,問題文中のみかん5個とりんご4個を買うと880円という記述を思い出しましょう。このことから,りんごが5個増えると値段が400円高くなるということがわかります。400円を4個で割ると100円になるので,りんごの値段は80円だとわかります。以上のことから,みかんは1個120円・りんごは1個80円となります。
A.みかん120円,りんご80円
このように割合が絡む発展した問題も,基本的な手順に忠実に解いていけば無事に答えを導けます。消去算でこれ以上にレベルの高い問題はなかなか目にしないので,どんな問題でも順序よく計算していくことを忘れないようにしましょう。
まとめ
今回は消去算の応用問題を取り扱っていきました。おさらいしておくと,消去算に出会ったら,片方のものの数を揃えて消去する→求めた値を活用して他方の値も計算するというステップに従うと解くことができます。是非復習を重ねて自分のものにしていきましょう。本記事が学習の手助けとなれば幸いです。
(ライター:大舘)
おすすめ記事
参考
- 粟根秀史,「中学入試 分野別レッスン 算数 文章題」,文英堂(2020)
- 古川俊,「差集め算・過不足算・つるかめ算・消去算」,Next Education(2018)
- access,「消去算―整数範囲:最小公倍数の計算が早く正確にできること」,認知工学(2012)
















