今回は旅人算の解き方をご紹介いたします。
旅人算とは動くものの速さを題材とする問題です。進行方向が同じ場合は出会い算,進行方向が違う場合は追いつき算という呼び方をすることもあります。中学入試の算数では頻繁に出題されるため,対策が欠かせません。
本記事ではその中でも,実際に入試に出題された問題を取り上げ,答えを解説しながら肝心なポイントを整理していくものになっています。ピックアップする問題はその中でも,グラフが関連する標準的な難易度のものであり,したがってこの記事はパターンの紹介というよりは実践問題集に近いです。
そのため基礎的な知識をあらかじめ身につけておくと分かりやすいと思われますが,初めて旅人算に触れる方でも理解しやすいように解説しております。よろしければ参考にしてみてください。
Contents
例題①
それでは早速,実際の入試の中からいくつかの問題を解いてみることにしましょう。第一問目は少し難しく感じるかと思われます。自分の力でまずは取り組んでみて,ヒントがあれば解けそうなのに…と感じた際には解説を参照しながら問題を進めてください。
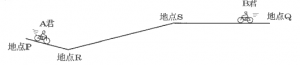
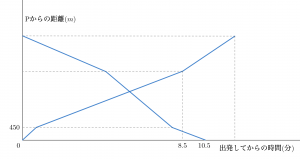
上図のように,地点P,Qの間をA君はPからQへ,B君はQからPへ自転車で向かいます。2人は同時に出発し,上り坂では毎分180m,下り坂では毎分450m,SとQの間は毎分250mの速さで進みます。下図はA君とB君が出発してからの時間とPからの距離の関係を表したグラフです。
(1)RからSまでの距離は何mですか。
(2)PからQまでの距離は何mですか。
(3)A君が出発してからQに到着するまでかかった時間は何分何秒ですか。
(4)A君とB君が出会ったのはPから何mの地点ですか。
(成城中学校(2016),一部改題)
解説①
情報を整理しよう
ここからは解説に移ります。さて,この問題を見ておそらくほとんどの方が「問題文が長いな」を思われたことでしょう。旅人算は特に問題文が長くなりがちです。文が長いとどこから手をつければいいのか分かりづらいです。そのためこのような問題では,まず情報を整理することが重要になります。
ではどの情報をどのように整理すればよいのでしょうか。その手順を以下でご紹介します。
ここで大事なのは「だれが」「どこを」ということです。今回は,AさんがP→R→S→Qと進みます。そしてその道のりの特徴と速度に注目すると,AさんはPからRまでの下り坂を毎分450mで進み,RからSまでの上り坂を毎分180mで進み,RからQまでの平坦な道を毎分250mで進む,ということが分かります。これが情報の整理です。
同じようにBさんの進み方をみていくと,BさんはAさんと逆向きにQ→S→R→Pと進みます。そして先程のように情報を仔細に整理すると,QからRまでの平坦な道を毎分250mで進み,SからRまでの下り坂を毎分450mで進み,RからPまでの上り坂を毎分180mで進むと分かります。これらをまとめると次の図のようになります。
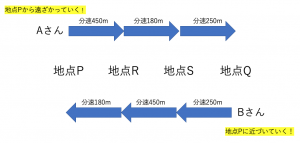
グラフと対比させよう
ではこのまとめた情報をもとに,グラフを眺めていきましょう。図で見たように,Aさんは地点Pから遠ざかっていき,Bさんは地点Pへと近づいて行きます。ここでグラフの縦軸がPからの距離を示していることを思い出しましょう。それらの折れ線の片方はPから0mのところから出発し,もう片方はPから0mのところに到着していました。このことから右上がりの線がAさんを,右下がりの線がBさんを表していることが判明します。
そしてそれぞれの線はどちらも3回折れているのですが,この変化が生じている理由も上の図を見るとはっきりと分かります。つまりこの線が折れるポイントが,Aさんであれば地点P・R・S・Qと,Bさんであれば地点Q・S・R・Pと対応しているわけです。
またそれぞれのグラフの正体・折れるポイントの意味が分かったら,縦軸と横軸の数値を合わせてさらに詳しく情報をまとめられます。ここではAさんはP からRまで450m進んだこととSまでに8.5分かかったことが,BさんはPに着くまでに10.5分かかったことが分かります。
設問を解こう
ここまでの情報を整理できたら,順番に問題を解いて行きましょう。
まず(1)を解く上で,Aさんのグラフに注目します。RからSまでの距離は,その間を進む速さが毎分180mと与えられているため,RからSまででかかった時間が分かれば求められそうです。ここでAさんはSまでに8.5分かかっているため,8.5-(Rまでにかかった時間)分がR→Sでかかった時間になります。
いまAさんがPからRまで450m進んでいることからPからRまでの間の距離は450mであることが分かり,下り坂では毎分450mの速さで進むため,PからRまででかかった時間は450÷450=1分となります。したがってAさんはRからSまで進むのに7.5分かかったことが判明するため,RからSまでの距離は180×7.5=1350mになります。
次に(2)を考えていきます。上よりP・R間の距離は450m,R・S間の距離は1350mだと判明しています。したがってSからQまでの距離が分かれば答えを導くことができそうです。
ここではBさんのグラフを見てみましょう。BさんはQからPまでの移動に10.5分費やしていました。このときS・R間,R・P間の距離と速さが分かっているため,それぞれにかけた時間が求められます。SからRまで進むのにかかった時間は1350÷450=3分,RからPまで進むのにかかった時間は450÷180=2.5分だと分かります。
したがってQからSまででかかった時間は,10.5-(3+2.5)=5分で,ゆえにS・Q間の距離は250×5=1250mとなります。これよりPからQまでの距離は,450+1350+1250=3050mです。これら2つの設問のように旅人算の問題では道のり・時間・速さを意識しつつ色々な角度から問題を考える必要があります。
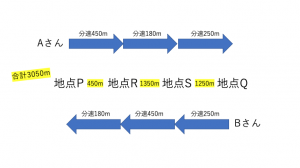
それでは(3)に取り組みましょう。AさんがQに到着するまでにかかった時間は,PからSまでの8.5分に,SからQまでにかかった時間を加えたものになります。いまS・Q間の距離は1250mであり,Aさんはその間を分速250mで進むことから,かかった時間は1250÷250=5分と分かります。したがってQまでにかかった時間は8.5+5=13.5分,つまり13分30秒です。
では最後に(4)を解いていきます。ここで 二人が出会う時間を□分後としましょう。ここで2人が出会っているのは,2本のグラフが交差している点から,地点Rと地点Sの間だと分かります。
Aさんは□分のうち最初の1分をP→Rの移動に費やすため,AさんはPから450+180×(□-1)mのところでBさんと出会います。他方Bさんは□分のうち初めの5分をQ→Sの移動に費やすため,BさんはQから1250+450×(□-5)m,つまりPから3050-{1250+450×(□-5)}mのところでAさんと出会います。そしてこの2つの距離が同じものを指すことから,次の式が成り立ちます。
450+180×(□-1)=3050-{1250+450×(□-5)}
この式を解くと,
450+180×□-180=3050-1250-450×□+2250
180×□+270=4050-450×□
630×□=3780
□=6
となります。このことから,AさんとBさんは6分後に出会うことが分かりました。よってこの値を□に当てはめると,2人が出会うのはPから450+180×(6-1)=450+900=1350mであると求められました。
A. (1)1350m,(2)3050m,(3)13分30秒,(4)1350m
まとめ①
- 旅人算の問題ではまず情報を整理しよう!
- グラフの線や点が何を示しているかを見極めよう!
- 「み・は・じ」を意識して色々な情報を少しずつ埋めていこう!
- 交差する問題では,かかった時間を□で表して考えよう!
例題②
それでは2問目に移ります。先程の図や解説を参考にしていただけたら幸いです。
ある駅の東口と西口をつなぐ連絡通路の一部に「動く歩道」があります。お父さんは歩く速さが毎分52mで,歩道だけを動きます。まさうみ君は歩く速さが毎分48mで,まず「動く歩道」上を歩き,「動く歩道」を降りてから歩道を歩きます。2人は西口から東口に向かって同時に歩き始めました。まさうみ君が「動く歩道」を降りたとき,お父さんは「動く歩道」の長さのちょうど半分にあたる地点を歩いていました。下のグラフは,2人の歩いた時間と西口からの距離の関係を表したものです。
(1)グラフの①に当てはまる数を求めなさい。
(2)「動く歩道」の速さは毎分何mですか。
(3)グラフの②に当てはまる数を求めなさい。
(4)「動く歩道」の長さは何mですか。
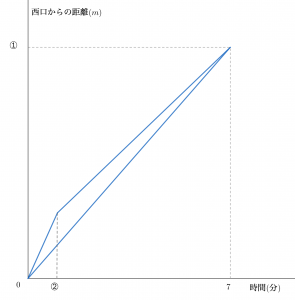
(成城中学校(2019),一部改題)
解説②
情報を整理しよう
では解説に移ります。今回はグラフが分かりやすいものでしたが,速度がキリのいい数字ではないので計算ミスがおきやすかったかもしれません。
先ほどの問題同様に問題の整理から始めていきましょう。今回出てくるのはまさうみ君とお父さんであり,旅人算の中でも同じ向きに進む追いつき算というものです。まさうみ君は毎分48m,お父さんが毎分52mで進みます。このときまさうみくんだけ「動く歩道」の上を歩くので,「動く歩道」の上を歩くときは毎分(48+「動く歩道」の速さ)mで進むことになります。
そしてグラフとこれらの情報を照らし合わせていきます。グラフ上の2本の線のうち,上の線だけ1回折れていますね。対して下の線は1回も折れない真っ直ぐな直線です,これより上の線が示す人が歩いているうちに1回速さが変わったことが分かります。つまり上の線が,「動く歩道」と歩道とで歩く速さが変わったまさうみ君を指していると判明します。このとき下の線はお父さんを指しています。そして2人とも7分後に東口に着いた,と考えられます。また問題文中の,まさうみ君が「動く歩道」を降りたとき,お父さんは「動く歩道」の長さのちょうど半分にあたる地点を歩いていた,という記述も重要です。
設問を解こう
これらの情報にしたがって設問を順番に解いて行きましょう。まず(1)の①に当てはまる数です。このときに重要なのが,まず①がどんなことを示す数字になるのかという見通しを立てることです。①は2人が歩き終わった地点が西口からどれくらい離れているか,つまりは西口と東口との距離を指します。
ここでお父さんのグラフに注目しましょう。お父さんは西口から東口まで分速52mで7分間歩きます。これらのことから西口と東口との距離は,52×7=364mとなります。
次に(2)の「動く歩道」の速さについて考えます。いま,まさうみ君が「動く歩道」を降りたとき,お父さんは「動く歩道」の長さのちょうど半分にあたる地点を歩いていたことから,このときまさうみ君の進む速さはお父さんの進む速さの2倍になっています。お父さんは毎分52mで歩いているため,まさうみ君の進む速さは毎分104mとなります。
ここでまさうみ君が「動く歩道」の上を歩いている,ということが重要です。これより先ほど見たように,まさうみ君が「動く歩道」上を進む速さは毎分(48+「動く歩道」の速さ)mとなります。これより48+「動く歩道」の速さ=104という式が立てられ,これを解くと,「動く歩道」の速さは毎分56mと求められました。
では続いて(3)を解いていきましょう。ここでも②が表す数値の意味を初めに考えます。②はまさうみ君のグラフの折れるポイントを示していますが,これより②はまさうみ君が「動く歩道」を降りたときの時間を表すと分かります。
ここでまさうみ君が□分に「動く歩道」を降りたとしましょう。まさうみ君は西口から東口までの364mを7分で進みます。いま,「動く歩道」の上は毎分48+56=104mで,歩道の上は毎分48mで進むと分かっているので,まさうみ君が進んだ距離について次のような式が成立します。
104×□+48×(7-□)=364
56×□+336=364
56×□=28
□=0.5
よってまさうみ君は歩き始めて0.5分後,つまり30秒後に「動く歩道」を降りると計算できました。したがって②には0.5という数字が入ります。
では最後に(4)を解きましょう。「動く歩道」の長さですが,ここで「動く歩道」に乗るときのまさうみ君に注目します。(3)で見たように,まさうみ君は「動く歩道」に0.5分間乗り,そのときの速さは毎分104mでした。このことから「動く歩道」の長さは104×0.5=52となります。
A. (1)364,(2)毎分54m,(3)0.5,(4)52m
まとめ②
- グラフの穴埋め問題では,そこに入る数字の意味に注目しよう!
最後に
今回は旅人算の標準的な問題をピックアップして,攻略法を解説していくものでした。問題文・図・グラフを行ったり来たりする必要があることから,慣れるまでは難しく感じるかもしれません。もし旅人算に出会ったら,今回見たようなヒントを活用してみましょう。
- 旅人算の問題ではまず情報を整理しよう!
- グラフの線や点が何を示しているかを見極めよう!
- 「み・は・じ」を意識して色々な情報を少しずつ埋めていこう!
- 交差する問題では,かかった時間を□で表して考えよう!
- グラフの穴埋め問題では,そこに入る数字の意味に注目しよう!
(ライター:大舘)
















