入試問題において水溶液の問題は,計算問題を作りやすいテーマでもあり,複雑な問題が作りやすく,非常に出やすいテーマです。ここではその1つである再結晶について学習しましょう。
Contents
溶解度と再結晶
溶解度
食塩や砂糖など,水に溶ける物質は多く存在します。実際に水に少し食塩を入れて混ぜると白い粉がすぐに消えるのを見たことがある人も多いことでしょう。もちろんこれは消えているわけではなく,目に見えないほどに細かくなってバラバラになっているだけです。
そのため食塩を入れる前に比べて,食塩を加えた後は,加えた食塩の分だけ水溶液が重くなっています。
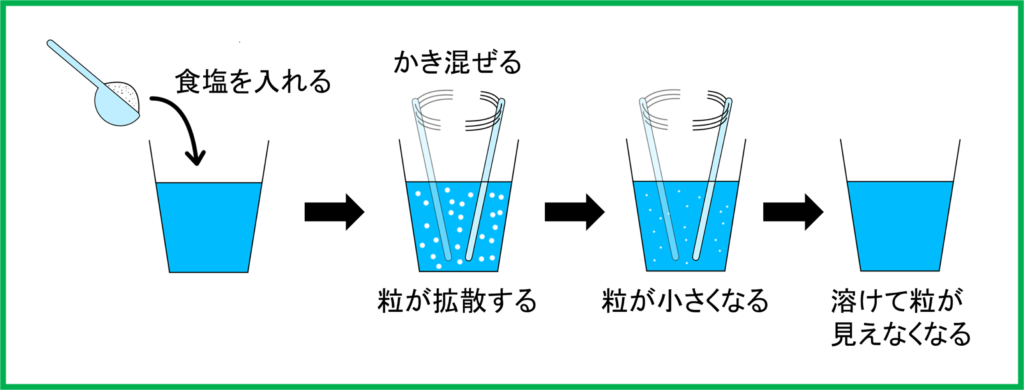
このようにして食塩は水に溶けるわけですが,さてここで水を混ぜながらどんどん塩を加えていったらどうなるでしょう。
入れては見えなくなってをずっと繰り返すのでしょうか。いいえ,そうではありません。
実はある量を境にして白い粉が消えずに見えるようになります。これは,それ以上水に溶けなくなったということです。

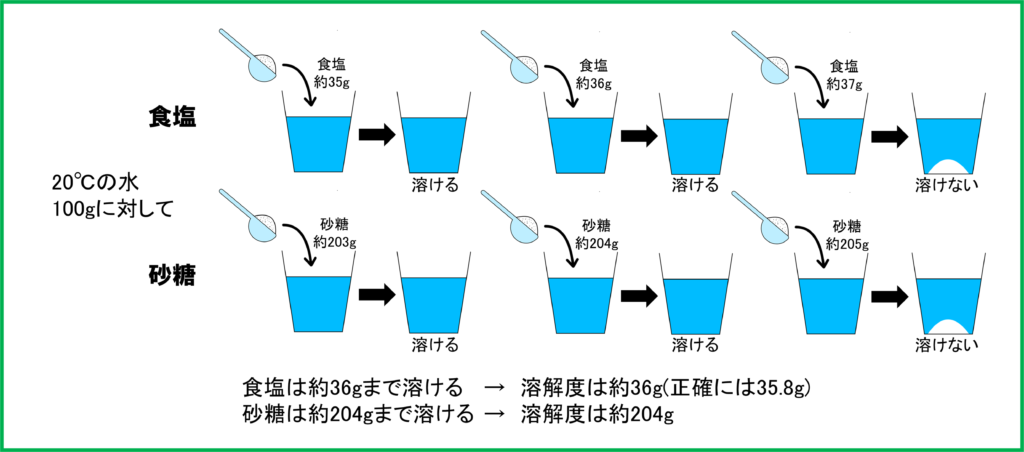
多くの場合,物質が水に溶けられる量には限界があるのです。しかし水の量も増えればもちろん溶けられる量も増えます。
水の量が2倍,3倍となれば,溶ける物質の量も2倍,3倍となる比例関係をもつのです。
そこで物質が水に溶ける量は,水100 gにその物質が何gまで溶けるのかという数字で表されることになっています。これを溶解度と呼びます。
さらに物質が限界まで水に溶けた水溶液のことを飽和水溶液と呼びます。
☆溶解度:その物質が水100 gに何gまで溶けるかを表したもの
☆飽和水溶液:物質が限界の量まで水に溶けている水溶液
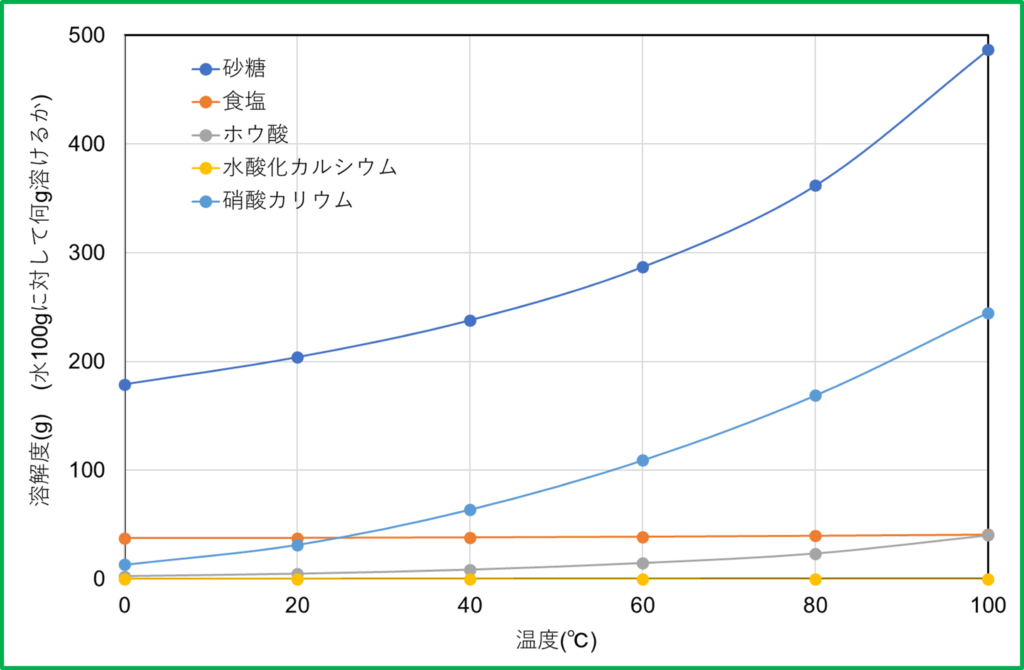
しかし同じ物質の溶解度であっても,実は温度によってその限界は変化してしまいます。そこで溶解度は,縦軸に「水100 gに溶ける量」,横軸に「温度」をとった曲線で表されることがあります。
曲線で表されるだけでなく,ある温度ごとに表で溶解度が表される場合もあります。
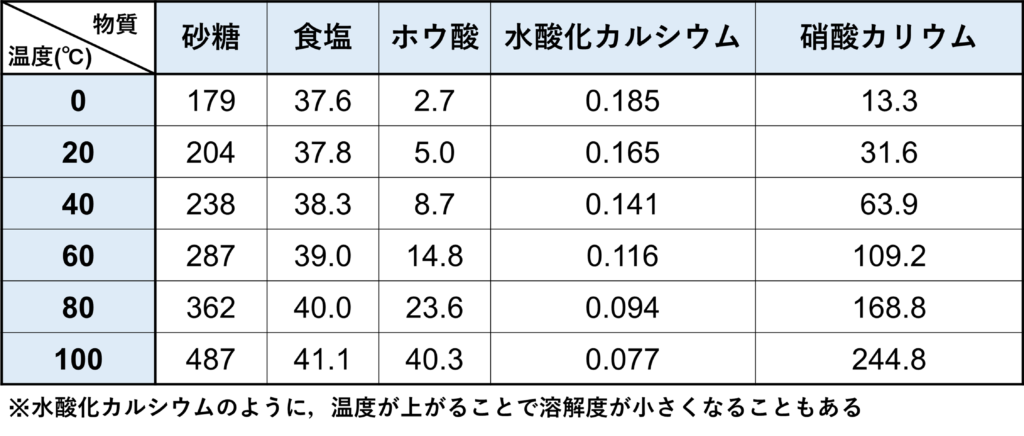
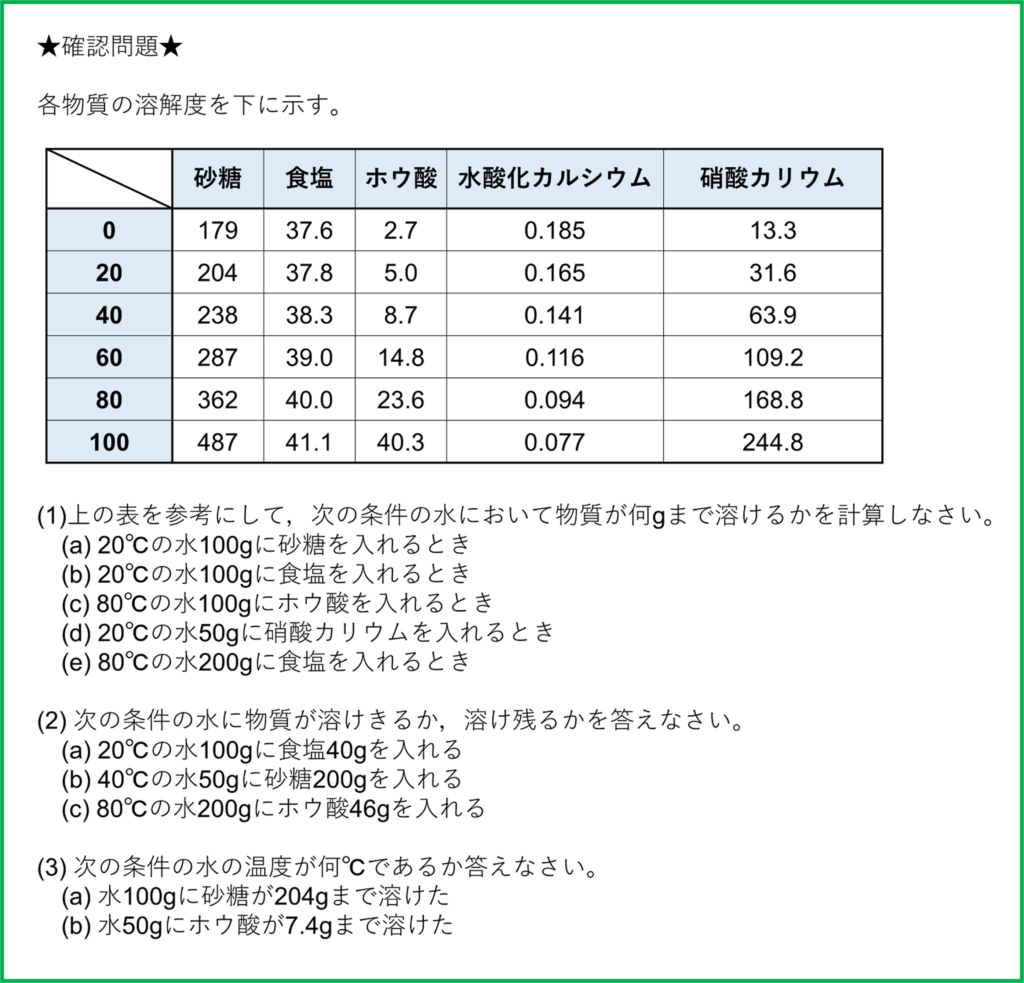
確認問題
解答
(1)
- (a) 204g
- (b) 37.8g
- (c) 23.6g
- (d) 15.8g
- (e) 80.0g
(2)
- (a) 溶け残る
- (b) 溶け残る
- (c) 溶けきる
(3)
- (a) 20℃
- (b) 60℃
解説
まず,溶解度は「その物質が水100gに対して何gまで溶けるか」という値であることを改めて確認してから問題の答えを見ていきましょう。
(1)
(a)
水は100gなので,表の砂糖の20℃の水に対する溶解度がそのまま答えとなります。よって204gまで溶けます。
(b)
水は100gなので,表の食塩の20℃の水に対する溶解度がそのまま答えとなります。よって37.8gまで溶けます。
(c)
水は100gなので,表のホウ酸の80℃の水に対する溶解度がそのまま答えとなります。よって23.6gまで溶けます。
(d)
「物質が水に溶ける量」は「水の質量」に比例します。
今,水が50gで,100gの0.5倍(1/2倍)なので,水に溶ける硝酸カリウムの量も,溶解度が示す値(水100gに溶ける量)の0.5倍(1/2倍)となります。
表から,20℃の水に対する硝酸カリウムの溶解度は31.6gなので,水50gにはその0.5倍(1/2倍)である15.8gまで溶けます。
(e)
(d)と同じように考えます。今,水は200gだから,これは100gの2倍。つまり水に溶ける食塩の量は溶解度が示す値(水100gに溶ける量)の2倍となります。
表から80℃の水に対する食塩の溶解度は40.0gなので,水200gにはその2倍である80.0gまで溶けます。
(2)
(a)
水は100gなので,表の食塩の20℃の水に対する溶解度が溶けきれる食塩の量となります。
よって溶ける量の限界は37.6gなので,40gの食塩を入れると溶けきらずに残ります。
(b)
水は50gで,100gの0.5倍(1/2倍)なので,この水に溶ける砂糖の量は40℃の水に対する砂糖の溶解度238gの0.5倍(1/2倍)である119gまで溶けることになります。
よって200gの砂糖を入れると溶けきらずに残ります。
(c)
水は200gで,100gの2倍なので,この水に溶けるホウ酸の量は80℃の水に対するホウ酸の溶解度23.6gの2倍である47.2gまで溶けることになります。
よって46gのホウ酸を入れると溶けきります。
(3)
(a)
表から,砂糖の溶解度が204gであるのは水が20℃のときです。
(b)
水50gでホウ酸が7.4gまで溶けるということは,同じ温度においては水100gに14.8gまで溶ける,すなわち溶解度が14.8gということです。
表から,ホウ酸の溶解度が14.8gであるのは水が60℃のときである。
再結晶
次に溶解度という考え方がどのように活かされるのか,その一例を紹介します。
上で示したグラフを見ると,大体の物質は温度が上がると溶解度も大きくなることが分かると思います。そこで次のような場合を考えてみましょう。
今硝酸カリウムが限界まで溶けた80℃の飽和水溶液があるとします。これを20℃まで冷やすとどうなるでしょうか。
水溶液を冷やせば溶けている物質の溶解度も小さくなります。つまり溶けられる限界の量が少なくなるのです。
すると冷やすにつれて,もともと溶けていた物質が溶けきれなくなり,次第に出てきて目に見えるようになります。
このとき物質は溶けて細かくなっていたものが集まって結晶が作られているのです。
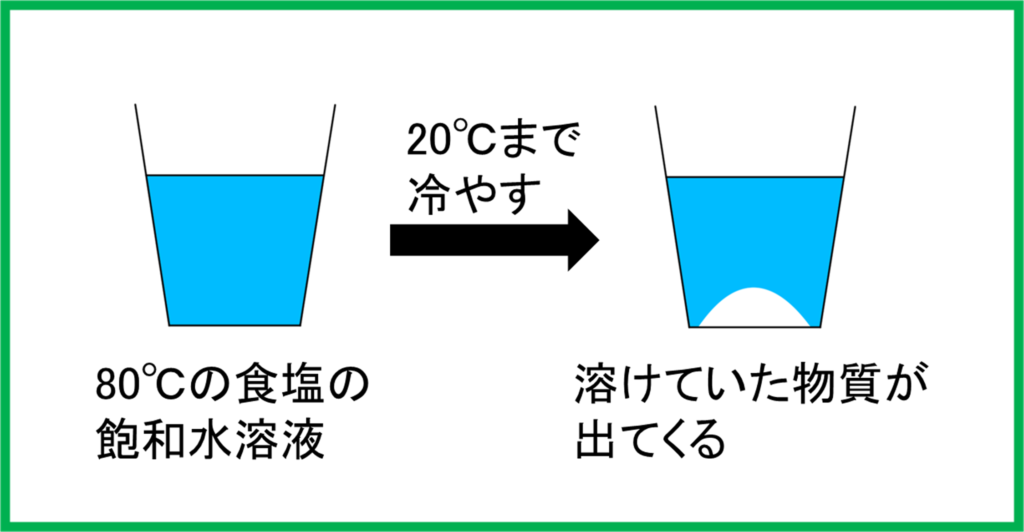
そしてこのとき出てくる結晶は非常に純度が高い状態であることが知られています。
このようにして一旦温度の高い水などに溶かし,その後温度を下げることで不純物の少ない結晶を手に入れる方法を再結晶と言います。
☆再結晶:物質の溶解度が温度によって変化することを利用し,一旦物質を溶かして溶液を冷やすことで目的の物質を純度の高い結晶として取り出す方法。
確認問題
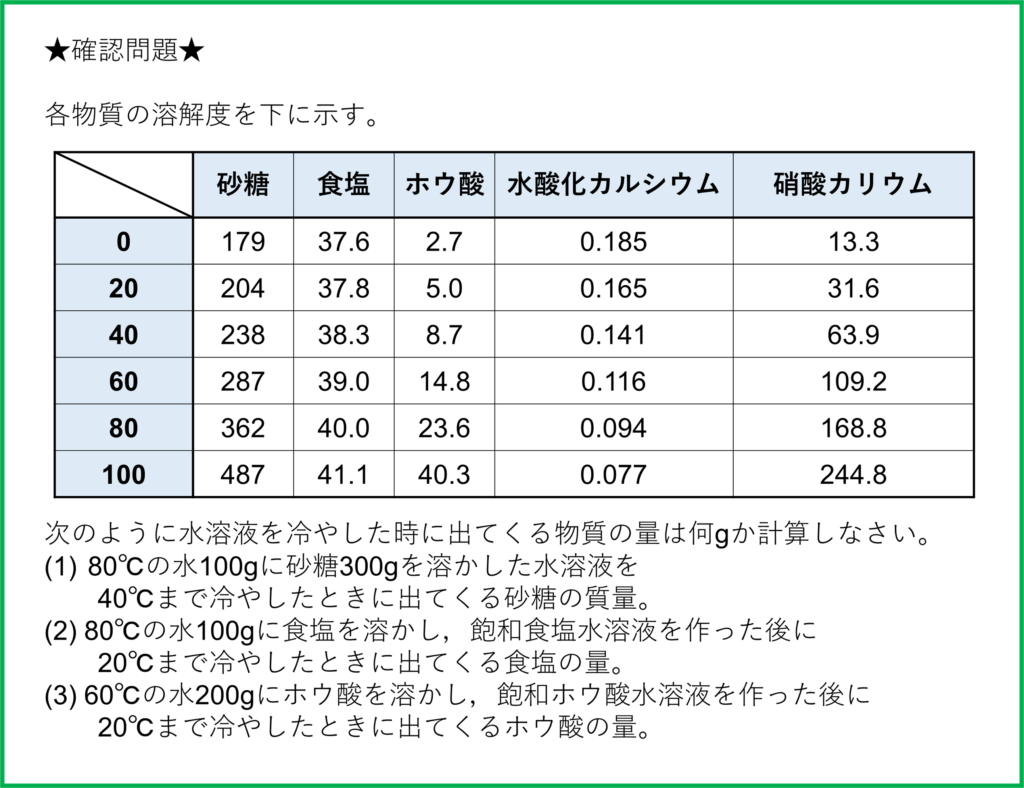
解答
- (1) 62g
- (2) 2.2g
- (3) 19.6g
解説
(1)
表から,40℃の水100gには,砂糖は238gまで溶けます。
もともと300gの砂糖が溶けた水溶液を冷やした時,238gまでは水に溶けた状態で,それよりも多い分だけ溶けきれずに出てきます。
よって300-238=62より,62gの砂糖が出てくることになります。
再結晶では物質が出てきますが,溶けた分が全部出てくるわけではないので注意しましょう。
(2)
表から,80℃の水100gには,食塩は40.0gまで溶けます。
よって問題にある80℃の飽和食塩水溶液には40.0gの食塩が溶けています。
また20℃の水100gには,食塩は37.8gまで溶けます。
この差の分だけ食塩が溶けきれなくなって出てきます。よって40.0-37.8=2.2より,2.2gの食塩が出てくることになります。
(3)
表から,60℃の水100gには,ホウ酸は14.8gまで溶けます。
今,水はもともとその2倍の200gあるので,ホウ酸もその2倍溶けることになります。
つまり80℃の水200gには14.8×2=29.6gのホウ酸が溶けることになる。
また20℃の水100gには,ホウ酸は5.0gまで溶けます。
上と同じように考えると,20℃の水200gには5.0×2=10.0gのホウ酸が溶けることになります。
この差の分だけ食塩が溶けきれなくなって出てきます。よって29.6-10.0=19.6より,19.6gの食塩が出てくることになります。
入試問題演習
それでは実際に出された入試問題を見てみましょう。
問題

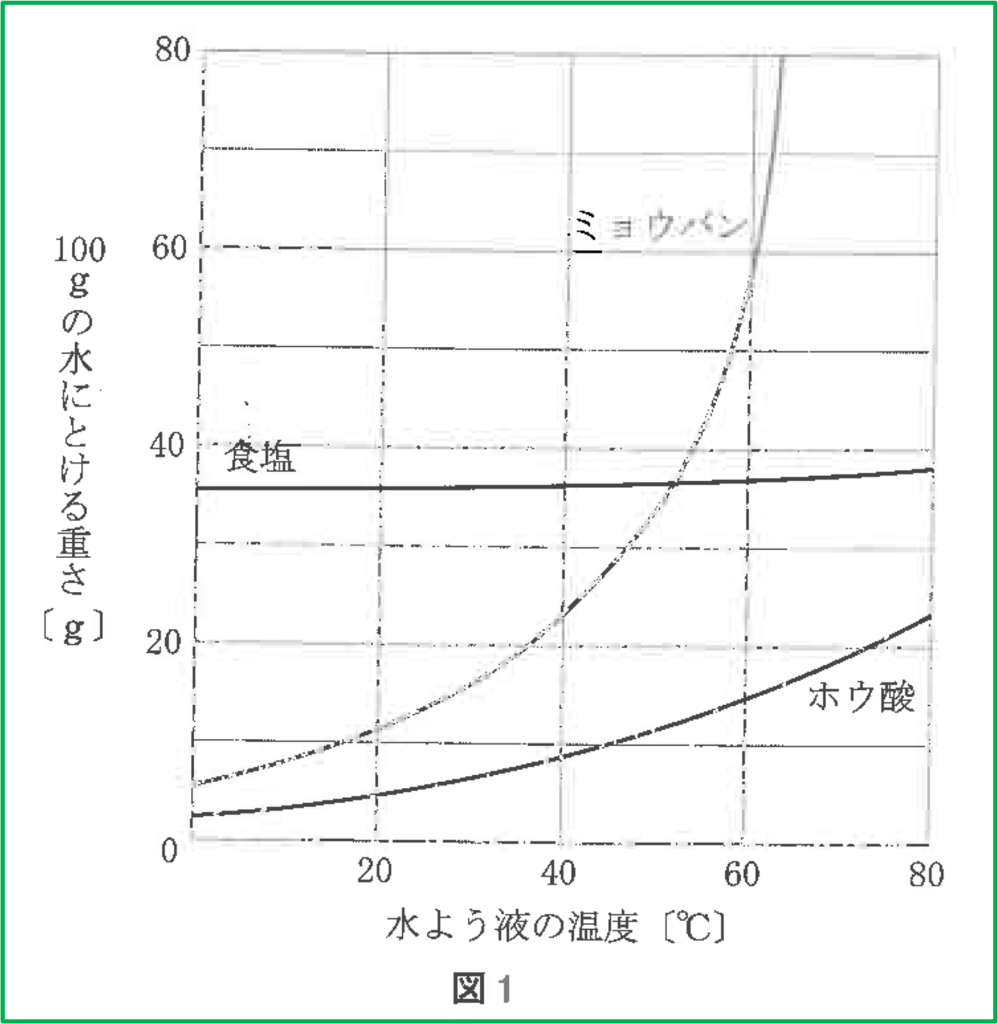
解答
- 問1 ミョウバン
- 問2 再結晶
- 問3 (ウ),(エ)
解説
問1
飽和水溶液において,冷やした時に出てくる物質の量は,「元の温度の溶解度」と「冷やした後の温度の溶解度」の差によって決まります。
しかし上の確認問題のようにその具体的な値を知る必要はありません。
図から60℃の溶解度と20℃の溶解度の差はミョウバンが1番大きくなっているのは明らかです。
よってミョウバンが冷やした時に1番多くの固体が出てきます。
問題によってはこのようにほとんど目分量での判断が可能なものもあります。具体的な計算が必要かそうでないかをしっかり見分けましょう。
問2
上で解説したように,一旦温度の高い水などに溶かし,その後温度を下げることで不純物の少ない結晶を手に入れる方法を「再結晶」といいます。
問3
(ア)
水溶液の濃度は水のどの部分でも一定です。上と下で違いはありません。
(イ)
水溶液を濾過してもろ紙の上には何も残りません。ろ過は溶けきれてない物質だけを回収できます。溶けた物質は水とともにろ紙を通過します。
(ウ)
「無色」と「透明」は違います。
水溶液は透けて向こう側が見えます。このような状態を「透明」というのです。牛乳のように向こう側が見えない場合は「不透明」です。
溶かした物質によっては色が付くこともありますが,水溶液の場合は色が付いていても向こう側が見える「透明」の状態です。
(エ)
酸性やアルカリ性などの性質は溶けている物質によって変わってきます。
例えば塩化水素を溶かした時,水溶液は酸性となりますが,水酸化ナトリウムを溶かした時,水溶液はアルカリ性となります。
まとめ
再結晶は実際の実験においても用いられる重要な手法です。そして水溶液の性質は今後もさらに増え,複雑化します。問題においてそれらの可能性をしっかり考えてかつ使いこなせるように1つ1つ着実に,そして正確にその性質についての知識を身につけていきましょう。特に計算問題の解き方はしっかり把握し,計算速度の向上に努めましょう。


















