今回の記事では調べ・推理・計算の条件に関する分野を解説してくシリーズの第2本目として,順位に関する問題を取り扱っていきます。順位に関する問題は,前回扱った数の大小問題と同様,パズルやゲームの感覚に近い問題です。したがって普段と異なる頭の働かせ方をしなければならず,その点に苦しむ受験生も多い分野だと言えます。よろしければ本記事を読みながら,受験合格に向けて対策していきましょう。
Contents
前回の振り返り!分野の特徴を解説
順位の問題の解説を進める前に,まずは前回の記事の振り返りを行っていきます。前回の記事では調べ・推理・条件の整理が与えられた問題の条件をもとに推論を重ねて答えを導いていく分野であるという説明からはじめていき,その中に存在する数字の大小関係を考える数の大小問題の解き方を解説していきました。
このときご紹介した解き方が線分図によるものでしたね。はじめに一つ一つの条件を整理し,条件のうちいくつかのパターンが考えられるものがあればそれを残らず図に起こし,そうして生み出された線分図を複合させ,すべての条件に沿うような解答を考えていくことが大小問題攻略のコツでした。この線分図を使ったコツは,多少形は異なるものの,今回扱う順位の問題でも使っていくことになります。まだピンときていなからは,是非前回文の記事を見ながら読み進めていただけますと幸いです。
「順位の問題」とは?
さて,ここからは順位の問題とはいったいどのような文章題なのかについて解説していきます。順位の問題とは,その名の通り順位・順番についての問題です。前回の数の大小問題も大きい順/小さい順に並び替えるという意味では順位の問題の中の一つと言えるかもしれませんが,この2つの問題には登場するのが数か人かという違いがあります。数の大小問題で登場するのは数字であり,それがいくつ離れているのかといった要素をはじめとした観点から回答することが重要となっていました。しかしこの順位の問題で登場するのは人であり,和・差・積・商の4つが登場せず,その代わり他の人の順位との関係性であったり,以上/以下といった表現の条件だったりが記されているのが特徴的です。中学入試にてよく出題されやすいのは,次の例題のようなタイプの問題です。
A,B,C,Dの4人が障害物競走をしました。そのときの結果について,次のことがらがわかっています。
①DのすぐあとにBがゴールした。②Cは1位でも4位でもなかった。③Aより先にゴールした人が2人以上いた。
このとき,1位から4位までを順に答えなさい。
A,B,C,D,Eの5人で借り物競走をした。5人の順位について次のことがわかっている。
ⅰ)Cの順位はDよりも上である。ⅱ)Eの順位はCよりも上だが1着ではなかった。ⅲ)Bの順位はAよりも上である。ⅳ)同着の順位のものはいない。
このとき,次の推論から必ず正しいと言えるものを1つ答えなさい。
ア:Bは1着である。イ:Dは5着である。ウ:2着はCである。
このように競争したり対決したりした結果の順位や序列に関して与えられたいくつかの条件から求めていくのが順位の問題です。お堅い算数というよりはクイズやパズルのようなカジュアルな謎解きに近いですが,他の文章題と同様解けると解けないとでは点数に大きな差が出てきてしまいます。そのため周りの受験生と差をつけるためにも,この記事を通して理解を深めていただけますと幸いです。なおこの順位の問題および前回扱った数の大小問題の他にも,調べ・推理・条件の整理という分野では様々な問題が出題されます。今後も解説を続けていきますので,ぜひ一読してみてください。
順位の問題を解くには…?
それではここからは順位に関する問題の解き方をご紹介していきます。この問題を解く方法としては,表を使った解き方が挙げられます。この表とは参加者と順位で構成されるもので,条件から「ここには〇〇くん・さんは入らないだろう」と考えられるものに×をつけていき,最終的に残った枠から全ての条件に合致するように順位を割り振っていくというものになります。ただし,このように言ったものの実際に解答の例をみてみないと多くの人にとっては分かりづらいことでしょう。そこで今回は上でご紹介した例題を用いて,解答ステップをご紹介していきます。
A,B,C,Dの4人が障害物競走をしました。そのときの結果について,次のことがらがわかっています。
①DのすぐあとにBがゴールした。②Cは1位でも4位でもなかった。③Aより先にゴールした人が2人以上いた。
このとき,1位から4位までを順に答えなさい。
この例題をもとにして,表による解答方法を覚えていきましょう。
まずは表を作ろう!
まず大事になってくるのが,大元となる表を用意するということです。普通の図表の整理の問題とは必要となる表の形が若干異なってくるので,表くらい簡単に書けるという自信をお持ちの読者の方も多いでしょうが,順位の問題ではこうやって図を書いていけばいいのかというテンプレートを頭に入れておくといいでしょう。今回はAからDまでの4人が登場し,1位から4位までを決めるということなので,名前を縦・順位を横において表を作れるといいですね。

この図の中に条件の内容を書き込んでいくというプロセスで答えを導いていくのが表による解き方です。そして表ができたので,今度は1つ目の条件から順番に,その中身を表の中に書き入れていきましょう。まず条件①で分かっていることが「DのすぐあとにBがゴールした」というものです。この条件から,Bが4位ではないこと及びDが1位でないことが読み取れますね。それは,Bが4位だとDは存在しない5位に・Dが1位だとBは存在しない0位になってしまうからです。このように1つ目の条件からBとDの順位が特定できるわけではありませんが,ハズレを探すことは可能です。どうなったら不自然な結果になるかを考えていくといいでしょう。そしてこの結果を表に落とし込んでいくのですが,今回はBが4位ではないこと・Dが1位ではないことが分かったので,その欄に×を書き込んでおきましょう。

この調子で残りの条件も書き込んでいくことで,誰が何位かを導いていきます。続いて2つ目の条件である「Cは1位でも4位でもなかった」に注目していきます。これはそのまま,Cの列の1位・4位に×を書き込んでいけばいいですね。このように条件を整理していく問題では,ときに簡単で分かりやすい内容のものも登場します。簡単なものは手早く対処して,計算スピードの向上に繋げていきましょう。

さて次に3つ目の条件である「Aより先にゴールした人が2人以上いた」について考えていきます。これについてはAが1位と2位ではないことと同じ意味を指しますね。色々な条件の中にはこのように「ゴールした人が……」といった若干遠回しな表現が含まれるものもあります。惑わされないように気をつけていきましょう。

このようにそれぞれの条件を確認することで表を埋めることができました。あとはこの表を眺めながら,順位を埋めていけばいいですね。この表を使った解き方のいいところは条件を簡単に整理できる点にあります。問題文と手元のメモを行ったり来たりしなくていいのは大幅な時間の短縮につながりますので,解き方の参考にしてみてください。話が逸れてしまいましたが,この表からまず判断できるのは1位に該当するのはBしかいないということです。それゆえ表のBの1位の欄に印をつけて,答えをメモしておきましょう。

表をもとに順番を求めよう!
ここまで分かれば後は芋づる式に答えを導いていけますね。1つ目の条件からDはBのすぐ後にゴールしたことが分かっているので,1位のBに続く2位はDだと判断できます。そして残ったAとCのうち,Cは4位ではないことから,3位がCで4位がAだと明らかになりました。このように手を動かしながら一つ一つの条件を確認していくことで,無事正しい答えに辿り着くことができます。慣れないうちは作業が億劫に感じるかもしれませんが,頑張って実力を伸ばしていきましょう。

A.B→D→C→A
練習問題を解いてみよう!
それでは解答の一連の流れが分かったところで,続いて先ほどご紹介した問題の2つ目を練習問題として取り上げながら,表の作り方や解答の導き方について振り返っていきましょう。ここで,改めて問題を提示しておきます。
A,B,C,D,Eの5人で借り物競走をした。5人の順位について次のことがわかっている。
ⅰ)Cの順位はDよりも上である。ⅱ)Eの順位はCよりも上だが1着ではなかった。ⅲ)Bの順位はAよりも上である。ⅳ)同着の順位のものはいない。
このとき,次の推論から必ず正しいと言えるものを1つ答えなさい。
ア:Bは1着である。イ:Dは5着である。ウ:2着はCである。
練習問題解説
いかがでしたでしょうか。この問題は先ほどの例題と比べて参加人数が1人多い上に,かつ問題の形式も「正しいものを選びなさい」という方式になっており,やや難しく感じられた人も少なくないでしょう。しかし,そのような方でも解説をきちんと読んで理解す頃ができれば問題ありません。分かった人は自分の答えを見ながら,分からなかった人は自分の考えを辿りながら,一緒に確認していきましょう。まずは表の作成に取り掛かっていきます。今回は次のようなものを作ることができたらいいですね。ない今回の問題では4つ目の条件として「同着の順位のものはいない」ことが挙げられています。それゆえ1位から5位までを順番に表に書いていけばいいのですが,もし同着が存在する場合は表の書き方を少し変えなければなりません。中学受験で同着の場合が登場することは滅多にないので省略しますが,そういった問題もあることだけ頭の片隅に置いておくといいかもしれませんね。
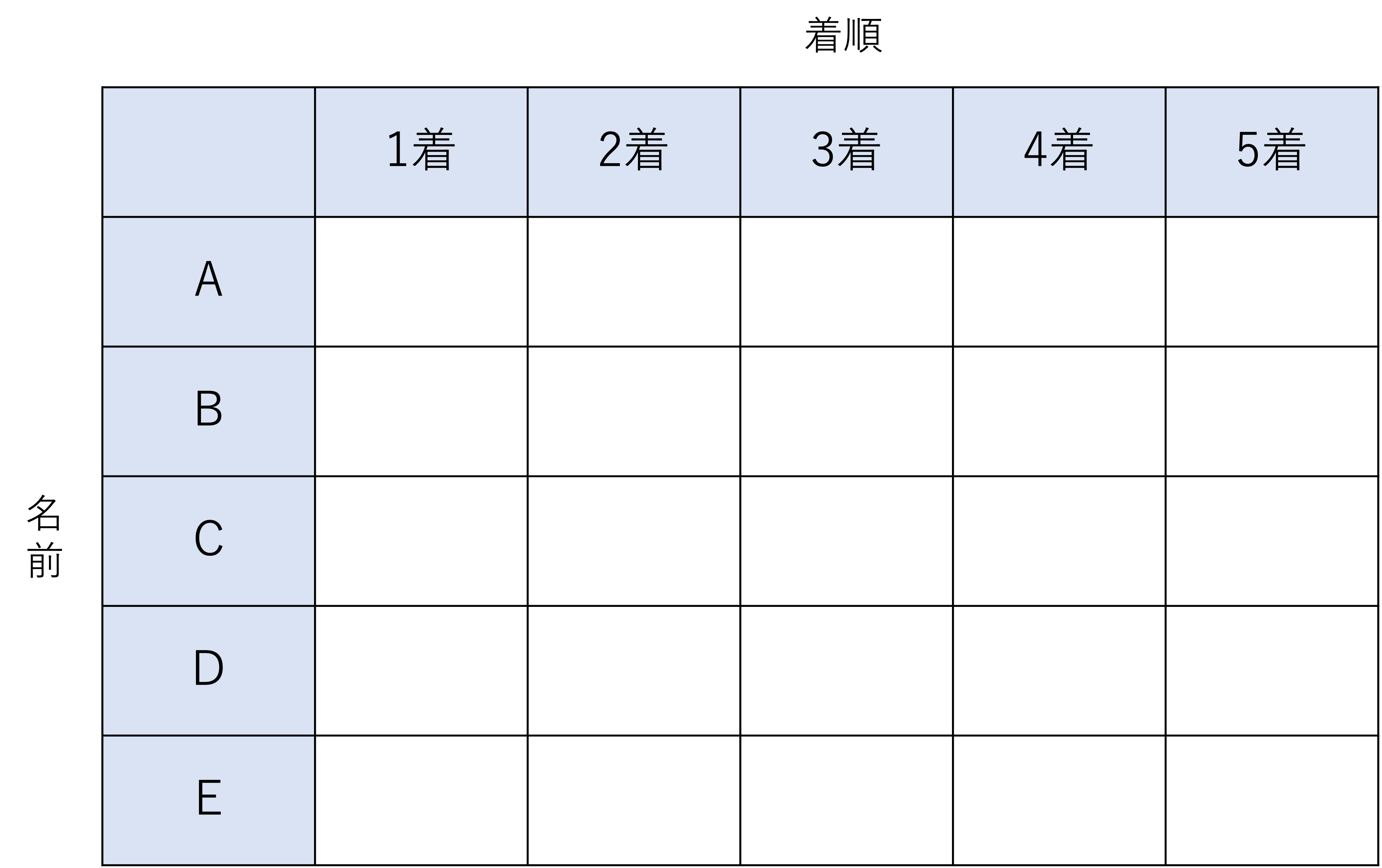
それでは条件を順に見ていき,不自然なマスに×をつけていきましょう。はじめに1つ目の「Cの順位はDよりも上である」に関してですが,この条件からは先ほどの問題と同じように考えると,Cは5着ではないこと・Dは1着ではないことが明らかになりますね。そして2つ目の「Eの順位はCよりも上だが1着ではなかった」ですが,このことからはEが1着でも5着でもないことが分かり,更にCについても,Eより後ろであることからCは1着ではないことが分かります。続いて3つ目の「Bの順位はAよりも上である」という条件からは,Bが5着でないこととAが1着ではないことが判断できます。4つ目の条件は表の作成のときに確認したことからこのステップでは不要となるため,後はこれらの3つの条件をもとに答えを考えていけばいいですね。ここで途中経過として表を×で埋めておきましょう。
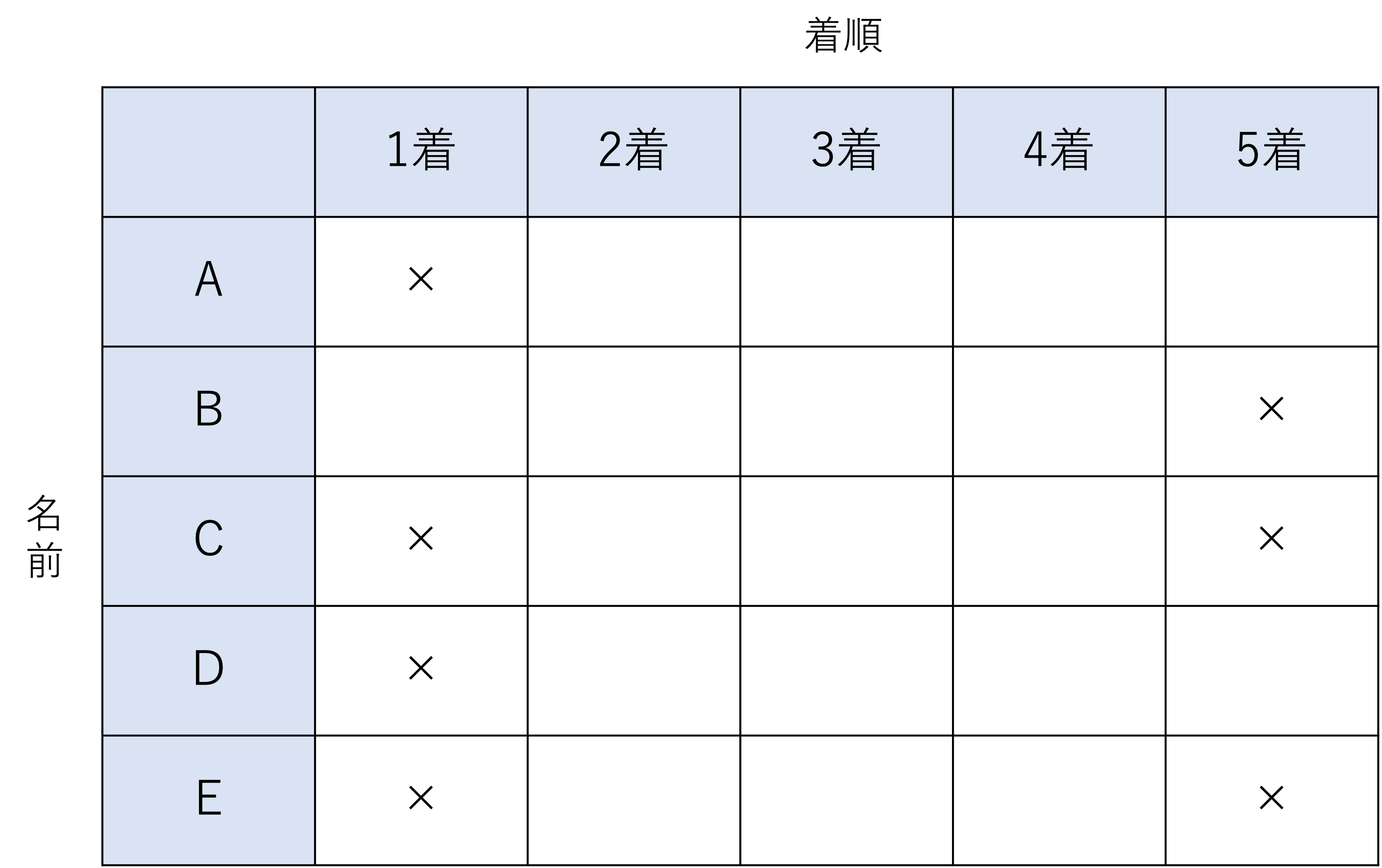
このように表に整理してみると,思っていたより埋まらないなと感じた人もいるのではないでしょうか。しかしこの練習問題は選択肢の中から合致するものを選ぶだけで解答が得られるものなので,この程度の情報量で正解に辿り着くことができます。
さて,ここからは3つの選択肢であるBは1着である・Dは5着である・2着はCであるのうちどれが正解なのかを考えていきましょう。まずはBの順位ですが,いま1着の縦の並びを見たときに,B以外の4人はすでに1着ではないことが分かっていますね。したがってアの選択肢が必ず正しいと言えることが明らかになります。
ちなみに残りの選択肢についても考えておきましょう。イの中身であるDの順位ですが,5着になる可能性があるのはAとDであり,必ずDが5着になるとは言えないためハズレになります。他方ウの中身ですが,こちらもCが2着になる可能性もある中,Cおよび1位のB以外の3人が2着になる可能性もあるため,必ずCが2着になるとは言えません。
このように選択肢の正誤をきちんと考えた上で答えを出すことが大切です。特に今回の問題は1つ目の選択肢であるアが答えだと早い段階で導かれてしまいますが,計算ミスが起きていたり答えが2つ存在したりすることもあるので,全ての選択肢をきちんと考慮していくことを忘れずに計算していきましょう。
A.ア
終わりに
今回の記事では順位の問題に関する解き方をご紹介していきました。この問題では表を使った解き方と図を使った解き方の2つで解答を導いていくことができるということが無事理解していただけたのなら幸いです。ただし,この記事だけで理解を完璧にしていくことは難しいでしょう。よろしければおすすめ記事や参考書籍を使いながら,更なる学力向上に励んでいきましょう。本記事がこの後の学習のお役に立てば幸いです。