前回，束縛条件とは設定に由来して物体の運動にかかる制限であることを説明した．特に計算上は，加速度に制限がかかることを見た．
今回は方程式の数と未知数の数に着目して，束縛条件が必要であることを見る．よく知られているように，方程式の数と未知数の数が一致していないと，未知数を完全に決定することはできない．そのため与えられた問題に対して，運動方程式を立てても，束縛条件を忘れていると，解くことができない．束縛条件によって加速度の制限の式が与えられ，問題が解けることを確認していこう.
より複雑な例
前回の記事よりは複雑な例を取り上げる．ここでは最後まで解ききることはせず，運動方程式を立て，束縛条件がどのように書かれるかまでに集中する．そこまで式が立てられれば，後は連立方程式を解く問題に帰着するので，難しくはないはずである．
例題1
以下の図1 のように，伸び縮みしない軽いひもに繋がれた，質量\(m_{1}\)の物体1 と\(m_{2}\)の物体2 がある．運動方程式と束縛条件の式を表せ．そして未知数の数と方程式の数が一致していることを確かめよ．
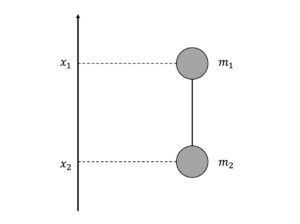図1: 伸び縮みしないひもに繋がれた2 物体
解答と解説
物体1 に働く張力を\(T_{1}\)，物体2 に働く張力を\(T_{2}\)とする．このとき2 つの物体の運動方程式は，
\(m_{1}a_{1} = -m_{1}g-T_{1}\), (1) \(m_{2}a_{2} = -m_{2}g+T_{2}\) (2)である．
ここでひとつ注意点がある．問題集の解答などを見ると，上の運動方程式のように張力を別々の文字でおかず，\(T_{1} = T_{2} = T\)と，はじめから同じ張力\(T\)が2 物体に働いているとしている．結果的にはそれで正しいのだが，その理由をここで説明する．ひもに対する運動方程式を立てると，
\(m_{ひも}a_{ひも} = -T_{1}+-T_{2}\) (3)である．重要になるのが「軽い」ひもを用いていることである．軽いというのは，「質量を無視する」という意味である．そこで\(m_{ひも} = 0\)とすると，すぐに
\(T_{1} = T_{2} (= T とおく)\) (4)であることが分かる．つまり「同じひもに働く張力は等しい」とできるのは，ひもが「軽い」ことに由来している．そして多くの解答では，この部分を省略しているのである．もちろん慣れていればそれで良いのだが，ここでは未知数の数や方程式の数に着目しているので，敢えてこのことを説明した．
さて以上のことを用いると，運動方程式は
\(m_{1}a_{1} = -m_{1}g-T_{1}\), (5) \(m_{2}a_{2} = -m_{2}g+T_{2}\) (6)となる．この時点で未知数は\(a_{1}\), \(a_{2}\), \(T\)の3 つある．それに対して，方程式は2 つしかない．だからこのままだと解くことができない．
では束縛条件は何かと言うと，今までと同様に「ひもが伸び縮みしない」ことである．これを式で表すと，
\(x_{1}-x_{2} = const. \) (7)である1．変位の時間微分が速度，速度の時間微分が加速度であることを思い出そう．この式を時間で2 度微分すれば，
\(a_{1}-a_{2} = 0 \) (8)となる．これが必要な3 つ目の式である．これで未知数と方程式の数が一致する．
例題2
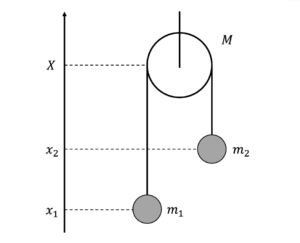図2: 動滑車と，それを介して繋がれた2 物体
以下の図2 のように，伸び縮みしない軽いひもに繋がれた，質量\(m_{1}\)の物体1 と\(m_{2}\)の物体2 があり，質量\(M\)の動滑車を介して吊るされている．動滑車は鉛直上向きの力\(F\)によって支えられている．運動方程式と束縛条件の式を表せ．そして未知数の数と方程式の数が一致していることを確かめよ．
解答と解説
まずは力を図示する．先程の例題で説明したように，軽いひもでつながれた物体には全て同じ張力\(T\)が働く．そのことに注意すると，以下の図3 のように表すことができる．
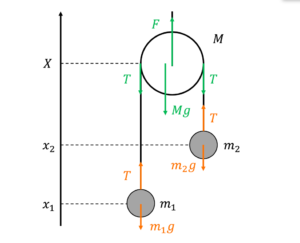図3: 動滑車と，それを介して繋がれた2 物体に力を図示したもの
それぞれの運動方程式は，
\(MA = F – Mg\), (9) \(m_{1}a_{1} = T – m_{1}g\), (10) \(m_{2}a_{2} = T – m_{2}g\) (11)である．未知数は\(A\), \(a_{1}\), \(a_{2}\), \(T\)の4 つである．よって方程式の数が1 つ足りない．
束縛条件は「ひもが伸び縮みしない」ことである．これを数式で表したい．動滑車と接触しているひもの長さを\(l\)，ひも全体の長さを\(L\)とすると，束縛条件は
\(\left( X-x_{1}\right) +\left( X-x_{2}\right) +l = L\) (12)と書ける．長さ\(l\)と\(L\)は定数2であるからまとめて
\(\left( X-x_{1}\right) +\left( X-x_{2}\right) = const.\) (13) \(2A-a_{1}-a_{2} = 0\) (14)と表せる．これに時間微分を2 回行えば，となる．これが束縛条件から得られる加速度に関する式で，未知数の数と方程式の数が一致することが分かる．
滑車の問題ではこの束縛条件の式を書き下すことが難しいと感じる人が多いかもしれない．多くの場合，ひもの長さが変わらないことから物体の位置に関する式を出し，その時間微分を考えることで加速度の式に帰着させるのである．問題集で滑車の問題を解く時に，束縛条件のことを意識しよう．
例題3
以下の図4 のように，斜面が水平方向から角度 だけ傾いている変形しない可動台上に，小球がある．その小球をそっと放すと，小球は台上を転がり落ちる．小球の位置は\(\left( x,y\right)\)で表し，始めの位置を\(\left( 0,0\right)\)とする．可動台の左端の位置は\(X\)で表し，はじめ\(X = 0\)であったとする．可動台や小球は空気抵抗や摩擦を一切受けないものとする．このとき，小球の加速度と可動台の加速度の間に成り立つ関係を求めよ．また小球は常に台上にあるものとする．
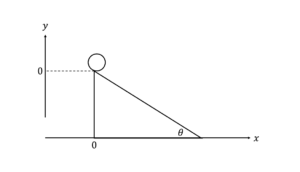図4: 可動台上を滑る球体．
解答と解説
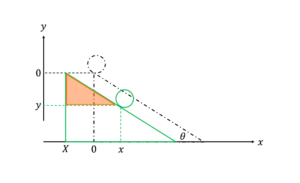図5: 初期状態から少し時間が経過した後の，可動台と球体の様子．
まず小球を放した後の状態を図示すると，図5 のようになる．束縛条件は，小球が変形しない可動台上を滑ることである．これは小球の位置と，可動台の位置の関係が常に，図5 のオレンジ色で塗った三角形を作ることにを意味している．もう少し言うと，小球の位置と可動台の位置が直角三角形の辺に相当しているため，三角比を用いることができる．数式としては，
\(\left| 0-y\right| = \left| x-X\right| \tan \theta\) (15)である．今，「辺の長さ」を考えているので，絶対値がつくことに注意しよう．しかしこの絵からすぐに分かるように，\(0-y > 0\), \(x-X > 0\) だからそのまま絶対値の記号は外せて，
\(0-y = \left( x-x\right) \tan \theta\) (16)となる．これを今までと同様に時間で2 階微分を施せば，
\(-a_{y} = \left( a_{x}-A_{x}\right) \tan \theta\) (17)
となる．ここで小球の加速度を\(a_{x}\), \(a_{y}\)で，可動台の加速度を\(A_{x}\)で表した．
簡単なまとめ
2 つの記事で束縛条件というものを具体例を交えて見てきた．束縛条件は教科書には明示的に書かれていないため，あまり意識しない人も多いだろう．しかし，今までも説明してきたように，束縛条件は問題を解くために欠かせない条件である．もし束縛条件を忘れていたら，方程式の数が足りなくなってしまう．特に，「ひもが伸び縮みしない」だとか「台が変形しない」など，さらっと書いてあることが条件になるので，見落としがちである．
また，束縛条件を使わないといないことが分かっていても，どのように式を立てたら良いか分からないということもあるだろう．そうならないためにも普段，問題を解く時から束縛条件を意識してほしい．多くの場合，束縛条件により物体の位置に制限を受けるので，それを時間で2 階微分するということを押えておくと良いだろう．
1const. は「定数」という意味．constant の略．
2動滑車が回っても，常に滑車の上半分のみがひもに接するので\(l\)は変わらない．
おすすめ記事
参考
こんにちは。慶應義塾大学大学院物理学科の花井遼介です。
中学から大学生の前半くらいまではバドミントンをずっとやっていましたが、途中から勉強や研究が忙しくなり、最近ほとんどやっていません。なかなか運動をする機会が減って残念ですが、時々自転車の乗って知らない場所に行ったり、散歩をしたりしています。(特に研究に行き詰ったとき……)昔から理科が好きで、高校生の時に聞いた、とある物理学者の講演に感動して以来、大学では物理を専門に学びたいと思っていました。現在は原子核理論の研究室に所属しています。その中でも僕は中性子星という超高密度な天体を、原子核理論の立場から研究しています。物理が好きでそれを専ら学んでいることもあって、高校生向けに高校物理や大学に入ってからの物理、物理学科についてなどの記事を提供していこうと思います。高校物理の記事でも、僕が大学に入って得た知識や理解をもとに、受験に役立つのみならず、学問としての面白さが含まれるような記事を書くつもりです。(受験向けの部分とそうでない部分は分かるように書くつもりですので、興味や必要に応じて読んでもらえればと思いま。)
僕の書く記事は、あくまで読者の皆さんの「補助的なもの」です。最終的には自分で勉強する、ということが大事になります。なので記事をきっかけに、皆さんが自分で物理を勉強できる状態になれれば、僕の目標は達成されたことになります。
僕の記事からさらに自分でもさらに深く勉強してほしいと思います。
皆さんと共に物理の面白さに触れ、理解を深められることを願っています。
