熱の移動と温度変化～カロリー計算に関する入試問題に挑戦しよう！その２～【中学受験理科】

以前の記事で、「熱の移動と温度変化」に関して、カロリー計算を中心とした入試問題の解説をおこないました。

カロリー計算に関する入試問題に挑戦しよう！　その１～【中学受験理科】

今回は、熱の移動や比熱などの問題についても、実際に出題された入試問題を解説します！　「熱の移動と温度変化」に関してまだ基礎がわかっていない……という人は過去の記事で解説しているので参考にしてください！　これらの予備知識がなくても解説では丁寧に知識の復習もおこないますので、実際に出題された問題の解説を理解しながら学習してもよいでしょう。

それでは早速解説していきます！

Contents

1 逗子開成中学校　2017年　一部改題
2 立教池袋中学校　2013年　一部改題
3 最後に
4 おすすめ記事
5 参考

逗子開成中学校　2017年　一部改題

問題

水の性質と熱の移り方について、下の問いに答えなさい。ただし、熱の出入りは湯と水の間のみとします。

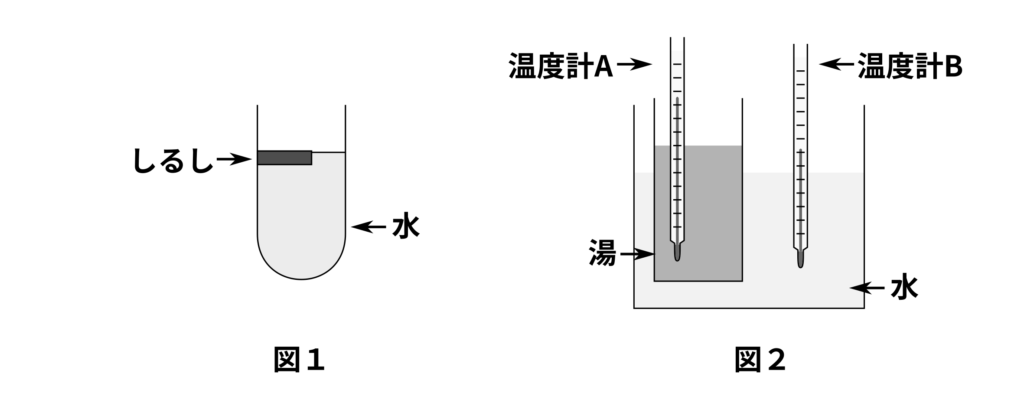
（１）　図１のように試験管に水を入れ、水面のところにしるしをつけた後、冷やして氷にしました。試験管の水が氷になったとき、その上の面はもとのしるしのところよりどのようになりますか。次のア～ウから選び、記号で答えなさい。

ア．上がる

イ．下がる

ウ．変わらない

解説

この問題は知識問題です。一般的に、水が氷になると体積が増えます。したがって答えは

ア．上がる

となります。

ただし、ここで注意が必要です。似たような問題で、水と氷がまじっている場合の水面の変化を答えさせる問題があります。この場合、氷がすべて水になっても、水面の高さは変わりません。このことを理解するには「浮力」の知識が必要なので、ここでは深く立ち入りませんが、気になった人は調べてみてください！

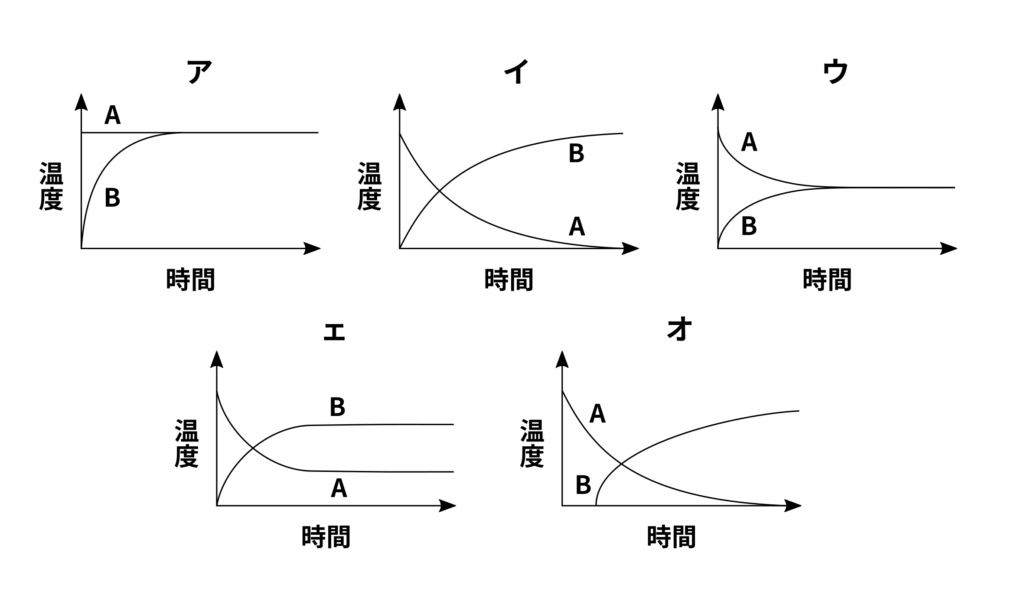
（２）　図２のように、水が入った大きいビーカーに、湯が入った小さいビーカーを入れ、湯と水の温度変化を調べました。図２の温度計A、Bは、時間にともなってどのように変わりますか。最も適したグラフを次のア～オから選び、記号で答えなさい。

解答

温度が違う２つの液体をつけてしばらく時間がたつと、２つの液体は同じ温度で一定の状態となります。そのため、答えはアかウのどちらかとなります。熱は温度の高い物質から温度の低い物質に移動するので、温度の高い物質の温度は低くなり、温度の低い物質の温度は高くなります。そのため答えは、

ウ

となります。

（３）　水\(1\,\mathrm{g}\)の温度を\(1\,{}^\circ\mathrm{C}\)上げるのに必要な熱量を、\(4.2\,\mathrm{J}\)（ジュール：熱量の単位）とします。\(50\,\mathrm{g}\)の水の温度を、\(10\,{}^\circ\mathrm{C}\)から\(30\,{}^\circ\mathrm{C}\)に上げるのに必要な熱量は何\(\,\mathrm{J}\)ですか。

解答

通常は水\(1\,\mathrm{g}\)の温度を\(1\,{}^\circ\mathrm{C}\)上げるのに必要な熱量を、\(1\,\mathrm{cal}\)として問題を解くことが多いですが、今回は\(\mathrm{J}\)での計算です。ジュールはカロリーと同じくエネルギーの単位なので、同じ計算方法で答えを求めることができます。\(50\,\mathrm{g}\)の水を\(10\,{}^\circ\mathrm{C}\)から\(30\,{}^\circ\mathrm{C}\)にするので、

\(50\,\mathrm{g} \times (30\,{}^\circ\mathrm{C} – 10\,{}^\circ\mathrm{C}) 4.2\,\mathrm{J}\,/\,\mathrm{g}\,\,{}^\circ\mathrm{C} = 4200\,\mathrm{J} \)

と求めることができます。

（４）　\(80\,{}^\circ\mathrm{C}\)の湯\(60\,\mathrm{g}\)に、\(10\,{}^\circ\mathrm{C}\)の水を混ぜて\(30\,{}^\circ\mathrm{C}\)にするためには、\(10\,{}^\circ\mathrm{C}\)の水が何\(\,\mathrm{g}\)必要ですか。

解答

この問題では、2つの物体同士の熱の移動を考えます。このとき、次の事実が重要です。

（物体Aが失った熱量）＝（物体Bが得た熱量）

この事実を念頭に問題を解きましょう。必要とする\(10\,{}^\circ\mathrm{C}\)の水が□\(\,\mathrm{g}\)であるとすると、\(80\,{}^\circ\mathrm{C}\)の湯が失った熱量と\(10\,{}^\circ\mathrm{C}\)の水が得た熱量はそれぞれ

\(80\,{}^\circ\mathrm{C}\)の湯が失った熱量……\(60\,\mathrm{g} \times (80\,{}^\circ\mathrm{C} – 30\,{}^\circ\mathrm{C}) \times 1\,\mathrm{cal}\,/\,\mathrm{g}\,\,{}^\circ\mathrm{C} = 3000\,\mathrm{cal} \)

\(10\,{}^\circ\mathrm{C}\)の水が得た熱量……\(\text{□}\,\mathrm{g} \times (30\,{}^\circ\mathrm{C} – 10\,{}^\circ\mathrm{C}) \times 1\,\mathrm{cal}\,/\,\mathrm{g}\,\,{}^\circ\mathrm{C} = \text{□}\times 20 \,\mathrm{cal} \)

となります。したがって、必要となる\(10\,{}^\circ\mathrm{C}\)の水の量は

\(150\,\mathrm{g}\)

と求めることができます。

（５）　\(80\,{}^\circ\mathrm{C}\)の湯\(50\,\mathrm{g}\)と\(50\,{}^\circ\mathrm{C}\)の湯\(100\,\mathrm{g}\)と\(10\,{}^\circ\mathrm{C}\)の水\(150\,\mathrm{g}\)を混ぜると、何\(\,{}^\circ\mathrm{C}\)になりますか。

解説

この問題では、3つの物体同士の熱の移動を考えます。このとき、次のように考えることができます。

3つ温度の水を一度に混ぜて十分時間がたったあとのの温度は、3つの温度の水のうち2つを混ぜて一定の温度にしたあと、もう1つの温度の水を混ぜて一定の温度にしたときの温度と同じです。つまり、一度に混ぜて問題を難しくしなくても、液体を順番に混ぜれば、通常の問題と同じように考えることができます。

まず、\(80\,{}^\circ\mathrm{C}\)の湯と\(50\,{}^\circ\mathrm{C}\)の湯を混ぜたあとの温度を求めましょう。この温度を△\(\,{}^\circ\mathrm{C}\)とします。\(80\,{}^\circ\mathrm{C}\)の湯が失った熱量と\(50\,{}^\circ\mathrm{C}\)の湯が得た熱量はそれぞれ

\(80\,{}^\circ\mathrm{C}\)の湯が失った熱量……\(50\,\mathrm{g} \times (80\,{}^\circ\mathrm{C} – \text{△}\,{}^\circ\mathrm{C}) \times 1\,\mathrm{cal}\,/\,\mathrm{g}\,\,{}^\circ\mathrm{C} = 50\times(80-\text{△}) \,\mathrm{cal} \)

\(50\,{}^\circ\mathrm{C}\)の湯が得た熱量……\(100\,\mathrm{g} \times (\text{△}\,{}^\circ\mathrm{C} – 50\,{}^\circ\mathrm{C}) \times 1\,\mathrm{cal}\,/\,\mathrm{g}\,\,{}^\circ\mathrm{C} = \text{100}\times (\text{△} – 50) \,\mathrm{cal} \)

となります。したがって、2つの湯を混ぜたあとの温度は

\(60\,{}^\circ\mathrm{C}\)

となります。次に、この\(60\,{}^\circ\mathrm{C}\)のお湯と\(10\,{}^\circ\mathrm{C}\)の水を混ぜたあとの温度を求めます。最終的な温度を□\(\,{}^\circ\mathrm{C}\)とします。このとき、\(60\,{}^\circ\mathrm{C}\)の湯が失った熱量と\(10\,{}^\circ\mathrm{C}\)の水が得た熱量はそれぞれ

\(60\,{}^\circ\mathrm{C}\)の湯が失った熱量……\(150\,\mathrm{g} \times (60\,{}^\circ\mathrm{C} – \text{□}\,{}^\circ\mathrm{C}) \times 1\,\mathrm{cal}\,/\,\mathrm{g}\,\,{}^\circ\mathrm{C} = 150\times(60-\text{□}) \,\mathrm{cal} \)

\(10\,{}^\circ\mathrm{C}\)の水が得た熱量……\(150\,\mathrm{g} \times (\text{□}\,{}^\circ\mathrm{C} – 60\,{}^\circ\mathrm{C}) \times 1\,\mathrm{cal}\,/\,\mathrm{g}\,\,{}^\circ\mathrm{C} = \text{150}\times (\text{□} – 10) \,\mathrm{cal} \)

となります。したがって、湯と水を混ぜたあとの温度は

\(35\,{}^\circ\mathrm{C}\)

と求めることができます。これが、3つの温度の湯と水を混ぜたあとの温度になります。

（６）　実験室のそうじをしていたところ、古い温度計が出てきたので、正しい温度を示すかどうか調べてみました。その結果、新しく正しい温度計が\(0\,{}^\circ\mathrm{C}\)および\(80\,{}^\circ\mathrm{C}\)を示したとき、古い温度計はそれぞれ\(2\,{}^\circ\mathrm{C}\)および\(78\,{}^\circ\mathrm{C}\)を示しました。この古い温度計が\(21\,{}^\circ\mathrm{C}\)を示すとき、正しい温度は何\(\,{}^\circ\mathrm{C}\)になりますか。

解説

この問題は、「熱の移動」と無関係ですが、比を使って簡単に解けるので、おまけとして解いてみましょう。

古い温度計と新しい温度計の関係を示したのが下の図です。

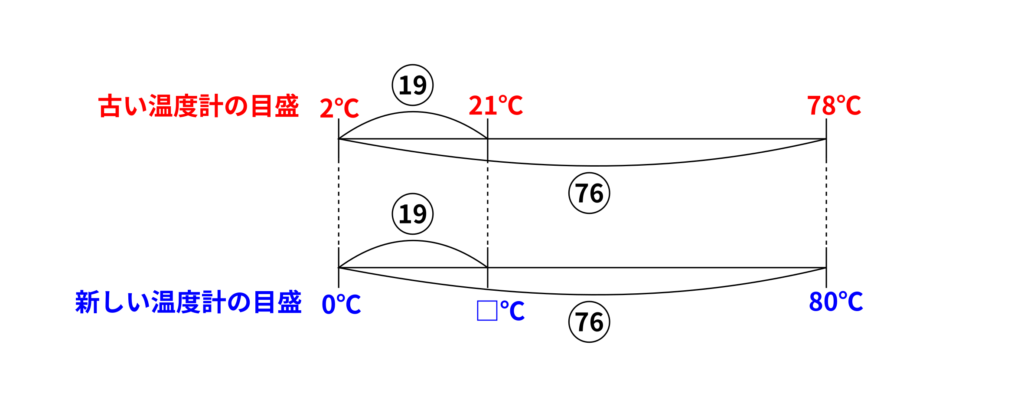
求めたいのは、古い温度計が示す\(21\,{}^\circ\mathrm{C}\)が、新しい温度計の何\(\,{}^\circ\mathrm{C}\)にあたるかです。この温度を□\(\,{}^\circ\mathrm{C}\)とすると、

古い温度計の\(2\,{}^\circ\mathrm{C}\)～\(21\,{}^\circ\mathrm{C}\)：\(2\,{}^\circ\mathrm{C}\)～\(78\,{}^\circ\mathrm{C}\)

新しい温度計の\(0\,{}^\circ\mathrm{C}\)～□\(\,{}^\circ\mathrm{C}\)：\(0\,{}^\circ\mathrm{C}\)～\(80\,{}^\circ\mathrm{C}\)

の二つは同じ比になります。したがって、

\( (80\,{}^\circ\mathrm{C}-0\,{}^\circ\mathrm{C}) \times \frac{21\,{}^\circ\mathrm{C}-2\,{}^\circ\mathrm{C}}{78\,{}^\circ\mathrm{C}-2\,{}^\circ\mathrm{C}} = 20\,{}^\circ\mathrm{C}\)

となって、答えが求まります。

立教池袋中学校　2013年　一部改題

問題

重さのちがう３種類の金属A・B・Cがあります。これらは鉄・銅・アルミニウムのいずれかで、同じ重さならば銅が一番温度が上がりやすく、アルミニウムが一番上がりにくいことが分かっています。これらの温度の上がり方を調べました。

水\(200\,\mathrm{g}\)の中に金属を入れて一定の割合で加熱し、\(20\,{}^\circ\mathrm{C}\)から\(70\,{}^\circ\mathrm{C}\)になるまでの時間をはかったところ表１のようになりました。

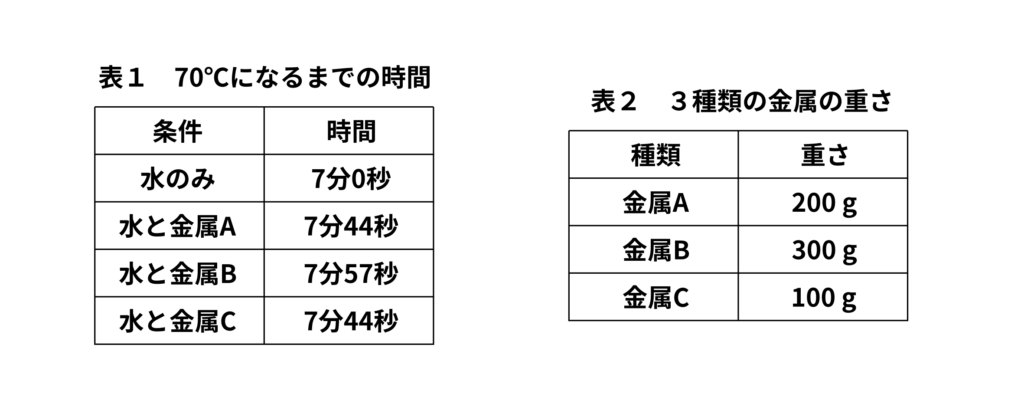
次に、それぞれの金属の重さをはかったところ表２のようになりました。

次の問いに答えなさい。ただし、容器の影響は考えなくてよいものとします。

1)　水・金属A・金属B・金属Cのうち、最も温度が上がりにくい性質をもつのはどれですか。次のア～エから選び、記号で答えなさい。

ア　水

イ　金属A

ウ　金属B

エ　金属C

解説

表１を見ると、水のみのときは7分、水と金属を同時に温めた場合は長くても7分57秒となっています。この場合、物質を温める順番は関係がありません。なので、水を7分で温めたあと、金属を57秒で温めたと考えてよいことになります。

また表２より、水の重さが\(200\,\mathrm{g}\)であるのに対して、いちばん重い金属Bも\(300\,\mathrm{g}\)程度です。このことから、同じ重さあたりで考えても、水を温めるのに必要な時間は、金属を温めるのに必要な時間に対してかなり長いことがわかります。したがって答えは

ア　水

となります。

このような物体の温まりにくさを表わす指標として「比熱」というものがあります。ある物質\(1\,\mathrm{g}\)の温度を\(1\,{}^\circ\mathrm{C}\)上げるのに必要な熱量をあらわしたものが「比熱」です。加熱時間と加えた熱量は比例関係にあるので、この問題の場合、加熱に長い時間がかかった水の比熱がもっとも大きいとわかります。したがって、水がもっとも温まりにくい物質なのです。実際、鉄の比熱は水の10分の1程度しかありません。

2)　水\(200\,\mathrm{g}\)の中に金属Aと金属Cをいっしょに入れて、はじめと同じ割合で加熱し、\(20\,{}^\circ\mathrm{C}\)から\(95\,{}^\circ\mathrm{C}\)になるまでの時間をはかりました。何分何秒でしたか。

解説

先ほども少し述べましたが、物体を温める順番は関係ありません。なので、

①　水\(200\,\mathrm{g}\)を\(20\,{}^\circ\mathrm{C}\)から\(95\,{}^\circ\mathrm{C}\)まで温める

②　金属Aを\(20\,{}^\circ\mathrm{C}\)から\(95\,{}^\circ\mathrm{C}\)まで温める

③　金属Cを\(20\,{}^\circ\mathrm{C}\)から\(95\,{}^\circ\mathrm{C}\)まで温める

という順番にしても必要な熱量は変わらないので、加熱時間も変わりません。

また、加熱にかかる時間は、物体の温度変化のみに比例し、物体の温度そのものには関係しません。つまり、表１より、水の温度を\(20\,{}^\circ\mathrm{C}\)から\(70\,{}^\circ\mathrm{C}\)にあげる時間は7分とありますが、この場合、水の温度を\(30\,{}^\circ\mathrm{C}\)から\(80\,{}^\circ\mathrm{C}\)に変化させても同じ7分だけ時間がかかります。以下では、このことを利用していきます。

まず、水を\(20\,{}^\circ\mathrm{C}\)から\(95\,{}^\circ\mathrm{C}\)まで温めるのに必要な時間を求めると

\(420\text{秒} \times\frac{95\,{}^\circ\mathrm{C} – 20\,{}^\circ\mathrm{C}}{70\,{}^\circ\mathrm{C} – 20\,{}^\circ\mathrm{C}} = 630\text{秒}\)

となります。次に、金属Aを温める時間を求めます。表１より、金属Aを\(20\,{}^\circ\mathrm{C}\)から\(70\,{}^\circ\mathrm{C}\)まで温めるのに必要な時間は、7分44秒から水を温めるのに必要な7分を引いて、

7分44秒 – 7分 = 44秒

となります。あとは水の場合と同様に、

\(44\text{秒}\times \frac{95\,{}^\circ\mathrm{C} – 20\,{}^\circ\mathrm{C}}{70\,{}^\circ\mathrm{C} – 20\,{}^\circ\mathrm{C}} = 66\text{秒}\)

となります。最後に金属Cですが、表１より、金属Aと同じ加熱時間なので、

\(44\text{秒}\times \frac{95\,{}^\circ\mathrm{C} – 20\,{}^\circ\mathrm{C}}{70\,{}^\circ\mathrm{C} – 20\,{}^\circ\mathrm{C}} = 66\text{秒}\)

となります。したがって、すべての物質を加熱するのにかかった時間は

\(630\,\text{秒} + 66\,\text{秒} + 66\,\text{秒} = 762\,\mathrm{秒} = 12\,\text{分}42\,\text{秒}\)

と求めることができます。

最後に

本記事では、「熱の移動と温度変化」に関する入試問題を解説しました！　基本的なカロリー計算や、3つ以上の物質の間の熱の移動、そしてあまり見かけることのない比熱に関する問題まで、いろいろなパターンの問題に慣れることができたでしょうか？　一回で解くことができなかったという人も、何度も同じ問題を復習することで、似たような問題にも対処することができます。決して出題頻度が高い分野とはいえませんが、もし出題されたときに差をつけられるように、一つ一つの分野の基礎をマスターしていきましょう！　それでは、引き続き受験勉強を頑張ってください！