中学受験を目指す受験生の中には、「平面図形が特に苦手・・・」という人も多いです。
- 「平面図形ってひらめきがないと無理なんでしょ?」
- 「図形のセンスがないと点数取れないんでしょ?」
と、諦めてしまうのはまだ早いです!
平面図形のひらめきというのは、「解法や補助線の引き方を知識として、素早く正確に取り出して活用できる」という意味です。知識と言っても暗記するというものとは性質が異なるため、「慣れる」という感覚が最も近いと思われます。
この記事では、平面図形を解くために知っておきたい「三角形の面積比と辺の比の基本」について説明していきます。
(なお、この記事では比の概念は理解している前提で話を進めていきます。)
Contents
まずは理解度をチェック!
難しく考えすぎていませんか?
平面図形を苦手とする人にありがちなのが、「難しく考えすぎている(=難しい問題だと思い込んでいる)」という点です。平面図形を見るときは、素直にシンプルに見ていくようにしましょう。
まずは高さの等しい三角形で見比べます。

「高さが等しい三角形は、面積の比が底辺の比と等しい」というのがお子さまには理解できているでしょうか?「そんなの、当たり前じゃん」という反応をする子と、「え、そうなの?」という反応をする子がいると思います。
前者であれば、この記事に書いてあることはすでに理解できているか、一度読めば理解できることだと思います。
後者の場合は、実際に高さを適当な数値で当てはめてみて、面積を計算させてみましょう。まずは一度「ああ、なるほど。たしかに。」と思わせてから先へ進まないと、何度やっても意味が分からない状態になってしまいます。
頭の中で図形を回転できていますか?
平面図形に苦手意識がある人は、向きが変わるだけで全く違うものに見えてしまうことがあります。
また、「地図が読めない」というタイプも多く、「頭の中で図形を回転させてみる」ということがうまくできないようです。
地図が読めない人でも、「自分の進行方向を上にして地図を見る」ということをすると、次にどちらに曲がればよいのかわかるようになる人が多いので、算数の平面図形でも同じように考えましょう。

右の三角形は、左の三角形の向きが変わっただけなので、面積比の考え方は左の三角形と同じです。
右の三角形の状態ですぐに面積比が答えられないのであれば、いったん12㎝と15㎝のところが底辺になるように向きを変えてみましょう。向きを変えてみると、左の三角形と同じ状態で見えるはずです。
この「実際に回してから見る」という経験を積むことによって、「頭の中で図形を回転させる」ということができるようになります。
図形を動かしている様子を視覚で捉えると、脳でそのときの視覚的イメージを記憶します。そのときの視覚的イメージを思い出すことによって、頭の中で回転させることができるようになるのです。
イメージが定着すると「前と同じように考えればいいんだな」という風に思えるので、実際に動かさなくても考えられるという状態になります。そのイメージが定着するまでは、図を実際に回してみる(テキストごと回して見る)のがよいでしょう。
台形の面積の求め方を理解していますか?
お子さんは台形の面積の求め方は知っていますでしょうか?
「(上底+下底)×高さ÷2」という公式ですが、もっと細かく表現すると「上の辺を底辺にする三角形と下の辺を底辺にする三角形に分けて考えた上で、面積はまとめて計算している」という状態です。
上向きの三角形と下向きの三角形でも、高さが等しければ面積の比は底辺の比に等しいという考え方が使えます。

ちなみに、台形の仲間には、平行四辺形が含まれますし、平行四辺形には長方形も正方形もひし形もすべて含まれます。
図形の名前が違うと全く別の物だと思ってしまっている人も多いのですが、人間でいうと「人間の中には日本人が含まれるし、日本人の中には関西人も関東人もいるよね」くらいの区別をしているだけにすぎません。
図形の特徴によって名前を変えているだけで、本質的なものはほとんど同じだと思って考えることができます。
基礎を組み合わせて考える
ここまで例に挙げてきたものが「うん、当たり前だよね」と理解できるようであれば、条件を増やした問題を考えてみましょう。
三角形を2つの三角形に分けた上で、片方の三角形をさらに2つの三角形に分けるという問題があったとします。この場合、面積比がどうなるのかを考えていきましょう。

全体を5:8に分けた三角形のうち、面積が「8」になった右側の三角形をさらに3:5に分けると考えます。ちょうど3と5でたして8なので、きれいに分けることができますが、問題の数値設定によっては小数や分数になるので、そこからさらに整数比に直すということが必要です。
このとき、例えば小数の比や分数の比を整数比に直すことができないとなると、図形ができるできないとはまた別の問題になります。それはそれで非常にまずい問題ですので、比の基本から学習しておきましょう。
面積比の求め方
上の図の中で、三角形ABDと三角形EDCはどちらも面積が「5」となり、面積の等しい三角形であることがわかりました。底辺の長さも高さも違うのに、面積が等しいというのはなぜなのかを考えてみましょう。
三角形の面積は、「底辺×高さ÷2」という公式で求めます。このとき、「底辺×高さ」が同じ大きさであれば、三角形の面積はどちらも同じ面積になるということがおわかりでしょうか。
「÷2」をする前に、もう同じであることがわかるので、三角形の面積比を考える場合には「÷2」をわざわざする必要がないですね。
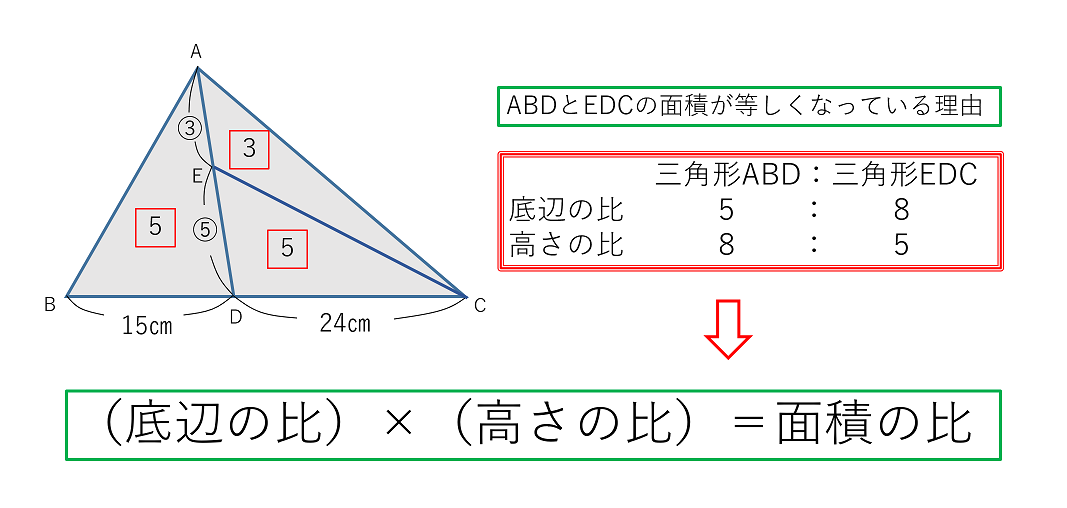
以上のことから、三角形の面積比を考える場合、「(底辺の比)×(高さの比)=面積の比」となることがわかります。
まとめ……の前に
登録6000人以上! 本サイト、中学受験ナビの監修も務めている『開成番長』こと繁田和貴が執筆する完全無料のメールマガジンでは、主に中学受験生のお子さんをお持ちの方へ向けた様々なお役立ち情報を配信中! さらに今なら登録者にはもれなく「開成番長・繁田監修 中学受験必勝の5箇条PDF」をプレゼント! 登録及び登録解除も簡単ですので、お気軽にご登録ください。

まとめ
ここまでが三角形の面積比の基礎部分と言えます。これに相似形などが加わって、少しずつ問題が複雑になっていきます。
この記事で確認したことが全て理解できるようになったら、こちらの記事で三角形の面積比の基本を学んでいきましょう。


















