過不足算・差集め算というのは,中学受験に登場する文章題の1つです。入試対策においてあまり重視されることはありませんが,それでもあらゆる中学校で登場しやすいものであり,しっかりと対策しておくことが必要です。
今回の記事では実際に中学入試で登場した問題を引用しながら,解き方や攻略法をご紹介していきます。そのため少し発展的な内容となりますので,「過不足算・差集め算とはどんなもの?」「どうやって解けばいい?」と疑問に思われている方は以前の記事をご確認ください。
Contents
解き方のおさらい!
それでは過不足算・差集め算の問題に挑戦…といきたいのですが,「最近触れていないから忘れてしまった」という人もいるかと思いますので,問題の攻略法について軽くおさらいしておきましょう。基礎はバッチリだ!という方にとっては読む必要のない内容ですので,練習問題に進んでください。
解くときのポイント① 情報を整理する!
過不足算・差集め算を解く,というよりは受験に登場する全ての文章題で共通して言える大切なことなのですが,問題で指定されている情報や条件を整理することが重要です。この情報をまとめるという作業を怠ると,正確な答えを出すことは難しいです。
それだけではありません。「試験・受験本番などでわからない問題に出会ったときは飛ばして次の問題に行こう!」というアドバイスを聞くこともあると思います。しかしこの次の問題に行く,ということについても,飛ばした問題の情報を整理できているといないとでは大きな違いが生まれます。全体像を掴めていないまま次の問題に行ってしまうと,何もわからないというモヤモヤを引きづってしまうことになります。このような点でも情報を整理することは不可欠です。
過不足算・差集め算では,個数・値段・人数などが問題文に登場します。例えば次のような典型的な問題を見てみましょう。
みかんがいくつかあります。これらを家族でひとり2個ずつ分けるとみかんは5個あまり,3個ずつ配るとみかんは1個足りません。このとき,みかんはいくつあるでしょう?
この問題では,みかんの個数・何個ずつ配るか・何個余る/足りないか・家族が□人という情報が登場しています。これらを整理すると下図のようになります。
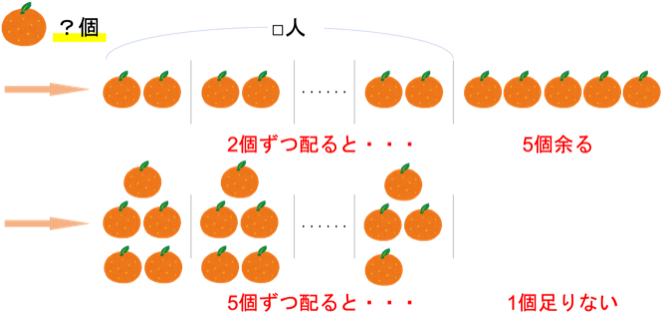
この問題はやや簡単なものであり,整理しなくてわかる人もいるでしょうが,図を書く習慣がついているのといないのと大違いです。ぜひこの記事を読んだその日から,図に整理することを習慣にしていきましょう。
解くときのポイント② 全体の差・1つあたりの差を考える!
次に大切なことが,全体の差と1つあたりの差を考えることです。これは過不足算・差集め算特有の解き方になりますので,以下引用する問題を解く方はこのステップを意識すると良いかと思われます。
まずはこの全体の差・1つあたりの差とは何か,という話になります。端的に行ってしまうと,全体の差とは,配るパターンAと配るパターンBではいくつ余る/足らない数が離れているか,ということを指します。この例題では2個ずつ配る場合・5個ずつ配る場合でそれぞれ5個余る/1個足りないという条件が出ているので,全体では6個離れていることがわかります。これが全体の差です。
1つあたりの差というのは,パターンAとパターンBとではそれぞれに対してどれくらいずつ配られる量に違いがあるのかということを意味します。別名で単位量あたりの差ということもありますね。この問題では1人に2個ずつ配る場合・5個ずつ配る場合が挙げられていました。そのため1人に配られる量は3個異なることがわかり,1つあたりの差は3個だと言えます。
このような部分に着目し,全体の個数だったり人数だったりを計算していきます。詳しい解説は過去の記事で取り上げていますので,よろしければそちらも合わせて参照してみてください。
問題① 基礎的なパターンの問題その1
それでは大体のポイントをおさらいしたところで,問題演習に移っていきましょう。最初の問題は先ほど出した例題と類似しているものになります。
50円切手と80円切手を同じ枚数だけ買いました。すると代金の差は540円でした。合わせて何枚の切手を買いましたか。
(跡見学園中学校(2014),一部改題)
解説①
それでは解説に移りましょう。上で説明したステップに従って,問題を攻略していきます。
まずは情報の整理ですね。今回の問題からは50円・80円という2種類の切手を□枚ずつ買うと540円の差があった,という情報が読み取れます。これらを例題で提示した図のようにまとめていきましょう。このとき全体での値段の差・切手1枚あたりの値段の差,つまりは全体の差と1つあたりの差にも注目しておくと,以降の計算が楽になります。下のような図が作れていたら完璧です。
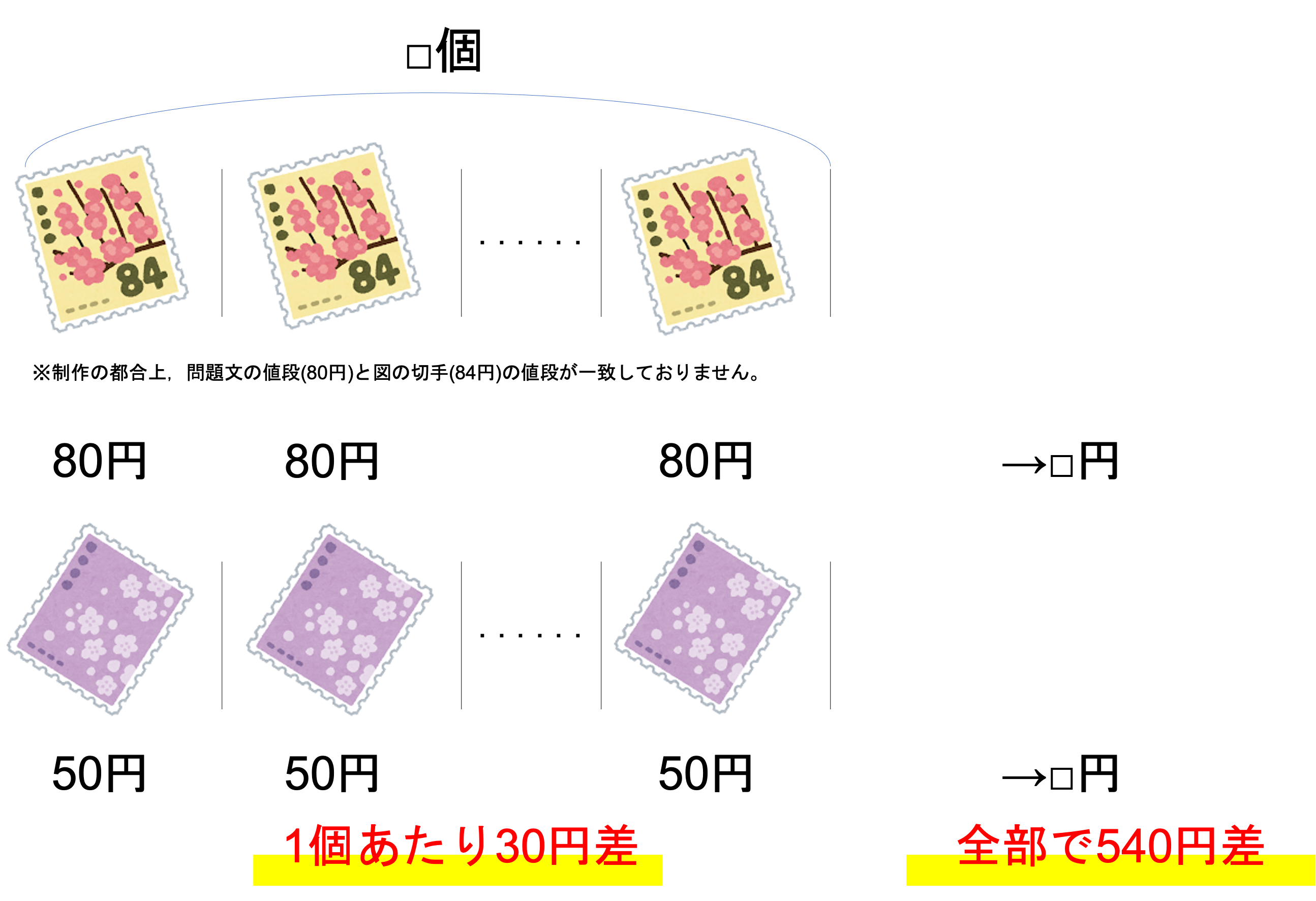
今回問題で聞かれていたのは切手を何枚買ったかということですね。この枚数についてですが,全体の差・1つあたりの差に注目すると,次の関係を見出すことができます。
1枚あたりの値段の差\(\times\)枚数=全体での値段の差
\(30\times\)□枚=540
この式を計算すると,□=18だと分かります。このことから50円切手・80円切手をそれぞれ18枚ずつ買ったことが求まりました。ただ今回は「合わせて何枚の切手を買いましたか」と聞かれているので,答えは18+18=36枚となります。
A.36枚
過不足算・差集め算は問題が単純なだけに,答え方で引っ掛けてくるパターンが多いです。計算が終わったからと言って気を抜かないようにしましょう!
問題② 基礎的なパターンの問題その2
では2問目に移りましょう。続いての問題も基本的なパターンからの出題となりますが,求めなければいけない部分が先ほどとは違います。この違いに注意して解いてみてください。
何人かの生徒が長いすに座るのに,1脚に5人ずつ座ると1人座れなくなります。また,1脚に6人ずつ座ると,5人しか座らない長椅子が1脚と,そのほかに長いすが1脚あまります。生徒は何人いますか。
(森村学園中等部(2014),一部改題)
解説②
ここからは2問目の解説に移りたいと思います。この問題は例題や1問目と似ているため,同じ容量で解いていけば正解が求められるかと思われます。
まずはやはり情報の整理からですね。今回の問題文に登場していた長椅子の数・余る/足りない人数・1つあたりの差・全体の差といった情報を整理すると,下の図のようになります。
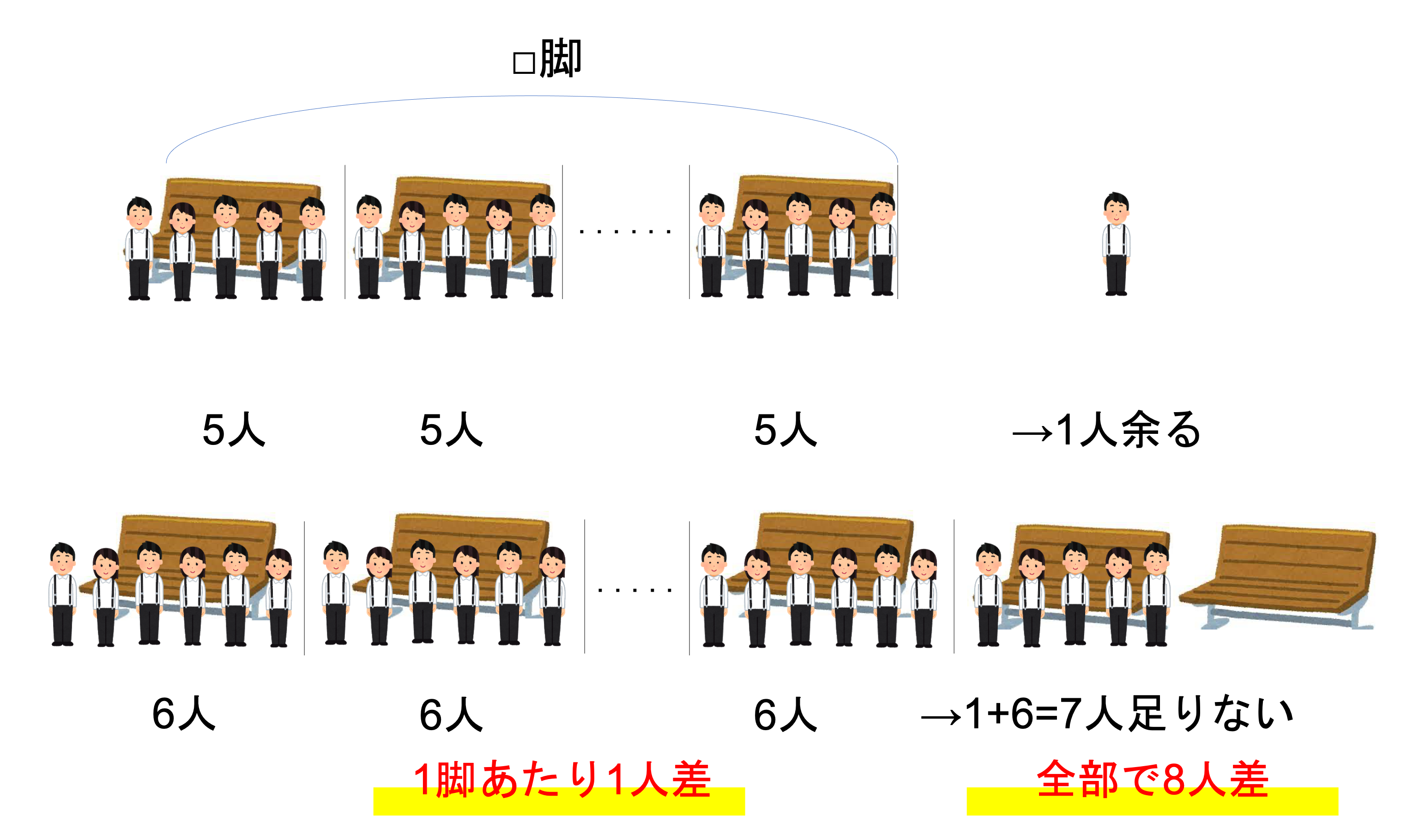
今回聞かれていたのは生徒の人数です。残念ながら生徒の人数をこの段階でいきなり計算することはできません。しかし長椅子の数が求められれば,次の関係から人数も計算することができますとわかります。
生徒の人数=椅子の数(times)5+1
生徒の人数=椅子の数(times)6-6
よってまずは椅子の数を求めましょう。この椅子の数は,先ほどの切手の枚数と同様に全体の差/1つあたりの差に注目すると導くことができそうです。上の図にも書きましたが,この問題では1脚の長椅子に5人が座るパターンと6人が座るパターンが登場していました。このことから1脚あたりに座る人数の差は1人だとわかります。
他方全体の差はどのようになっていたでしょうか。5人が座るパターンでは1人余ってしまい,6人が座るパターンだと2人分+1脚,つまりは7人足りないという指示が出ていました。このことから全体の差は8人だとわかります。
全体の差=1脚あたりの差\(\times\)長椅子の数
であり,全体の差も1脚あたりの差も求められたので,長椅子の数が計算できます。
8人=1(人)\(\times\)□脚
ゆえに椅子の数は8脚だと求められました。この値を先ほど見た関係に当てはめると,
生徒の人数=8(脚)\(\times\)5+1
生徒の人数=41
となることから,生徒の人数は41人だと答えが導かれました。
A.41人
問題③ 全体の個数に違いがある問題
それでは最後に全体の個数に違いがある問題に挑戦してみましょう。全体の数に違いが,と言われてもピンとこないかもしれませんが,一度問題を見てみるとご理解いただけるかと思います。
みかんとりんごがあります。みかんの数はりんごの数の2倍です。何人かの子どもたちにみかんを1人に5個ずつ,りんごを1人に4個ずつ配るとみかんは6個あまり,りんごは15個たりなくなります。りんごは何個あるでしょう。
(国府台女子学院中等部(2017),一部改題)
解説③
それでは最後の問題の解説に移りましょう。この問題ではみかんの数・りんごの数が違いました。今までの問題では切手だったり椅子だったりの数は固定されていましたが,今回はその要素が変わっているため,解きづらかったかもしれません。
ただどんな問題でもやはり最初に行うことは情報の整理です。今回出てきた情報を1つの図にまとめると,下のようになります。
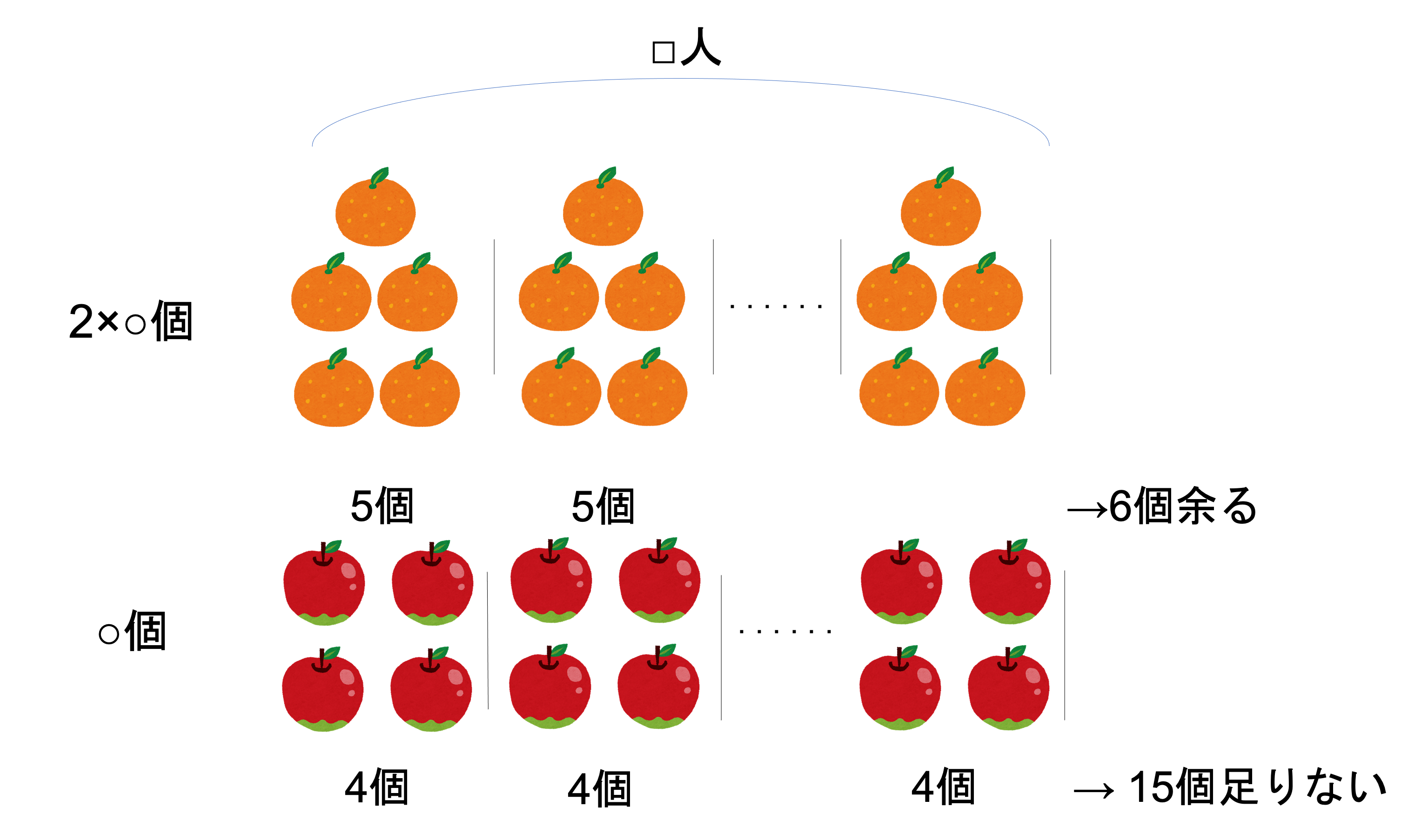
この図から一見1人あたり1個差・全体で21個差だと計算を進めたくなります。しかし1人あたり/全体という視点から全体の個数を求めることができるのは,全体の個数が揃っている場合だけです。みかんとりんごという2つのものを分けてはいますが,それらの全体の数が揃っていないので,計算することはできません。
しかし逆に言えば,全体の数を揃えることができれば過不足算・差集め算の要領で解くことができます。今回はりんごの数を2倍にして数を揃えればよさそうですね。
割り算において,割る数が変わらず割られる数が2倍になると,商と余りも2倍になります。この関係を活かすと,「○個のりんごを□人に4個ずつ分けると15個足りない」という条件を「2×○個のりんごを□人に2×4=8個ずつ分けると15×2=30個足りない」という条件に書き換えられます。これより情報を新しい図にまとめられそうです。
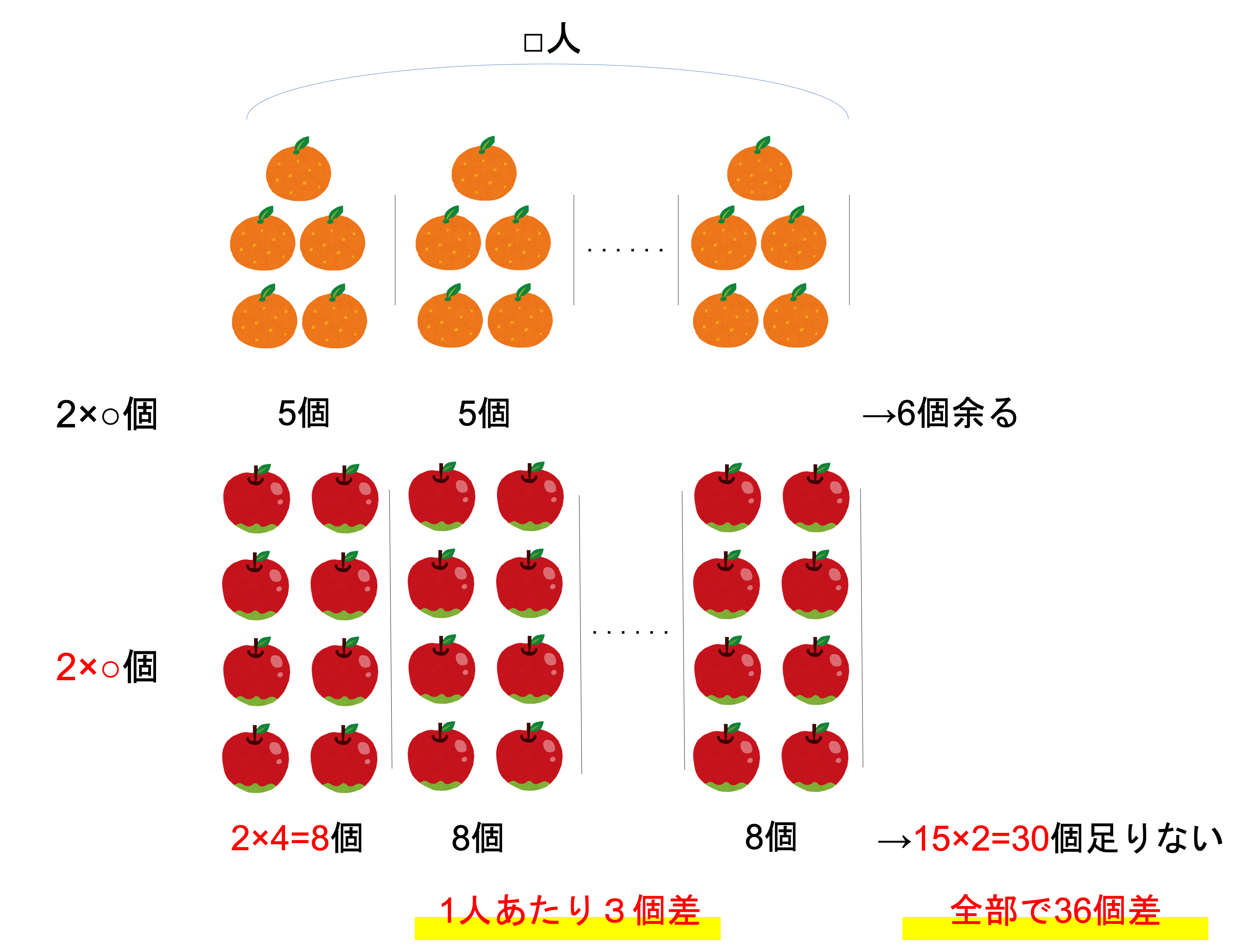
このようにして全体の個数を揃えられました。あとは通常の過不足算・差集め算と同じようにして解いていけばいいですね。いま1人に分けられる果物は3個差で,全体では36個差があることがわかっています。このとき全体の差・1人あたりの差・人数について次の関係が成り立つことから,子どもたちの人数を計算することができます。
全体の差=1人あたりの差\(\times\)子どもたちの人数
36(個)=3(個)\(\times\)□人
したがって子どもが12人いることが計算できました。あとはりんごを分けるときの個数や余りに着目して,りんごが全部で何個あるかを計算していきましょう。
4(個)×12(人)-15=33(個)
よってりんごの個数は33個になります。
A.33個
まとめ
今回の記事では過不足算・差集め算の応用問題について,実際に入試で登場した問題を交えながら解説していきました。問題をいくつか解いてみて理解していただけたかもしれませんが,受験における過不足算・差集め算は一筋縄でいかないことが多いです。それでも全体/1つあたりという個数の差に注目することは変わりません。これらのことを意識して,色々な問題を解いていきましょう。本記事が今後の学習の手助けとなれば幸いです。
(ライター:大舘)


















