場合の数・確率という単元は受験生が苦手としやすい単元です。それは樹形図や表などの考え方の多さと,数え間違いや重複,「並べ方」と「組み合わせ」の違いというややこしさにより正解がわかりにくいからです。
今回はそんな場合の数・確率という単元を,初めて聞く人にもわかりやすいように基礎的な単語から詳しく説明していきます。この分野は小問集合としても出題されやすいので,しっかりと点が取れるように対策しておきましょう。
Contents
基本事項の確認
場合の数とは?
まずは基礎的な用語の確認をしていきましょう。初めは場合の数についてです。場合の数とは,ある事柄が起こりうる場合の総数のことです。よく登場するのがさいころの出る目などですね。例えばさいころを1回振って4が出る場合の数,のように聞かれがちです。ちなみにこのときの場合の数は1通りです。これはさいころは1から6までの数しか存在せず,4はこの中に1つしか含まれていないからです。このように場合の数は○通りのように数え上げていきます。

確率とは?
続いて確率についてお話ししていきます。確率とは,ある事柄が発生する可能性のことを指します。この確率は分数で表します。このとき分数の分母には全ての場合の数が,分子には特定の事柄が起こりうる場合の数がきます。先程のさいころを1回振って4が出る,というケースについて,その確率という観点から改めて考えてみましょう。このときの全ての場合の数とは,さいころから出てくる可能性のある目がいくつあるか,ということと等しいです。今回は全部で6通りですね。(以降も特に言及しませんが,各目の出る確率は同様に確からしいという前提が必要です)このうち4が出る場合の数は,上で見たように1通りしか存在しません。したがって答えは\(\frac{1}{6}\)となるのです。
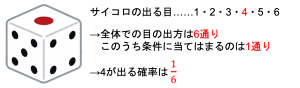
「並べる」問題の基本は樹形図!
ではさっそく場合の数・確率に関する簡単な問題を解いていきましょう。先程ご紹介したのはさいころ1つの例であり,まだ頭の中で計算が完結しやすいものでした。次にご紹介する例は,カードの並べ方になります。
{1,2,3}の3まいのカードを並べて,3けたの整数を作ります。3けたの整数は全部で何通りできますか。
この問題を解きながら,「並べる」問題の攻略法をご紹介いたします。そもそも「並べる」問題とは,文字通りある数字を順番に並べていく・数字の並び順が関係する問題のことです。今回は3けたの整数ということで,一の位・十の位・百の位という順番が存在していますよね。したがって「並べる」問題の典型例となるのです。
この問題を解くためには樹形図というテクニックが必要になってきます。樹形図とは,物事を順番に書き出して数え上げる手段となります。枝分かれしている様子が木のように見えるので樹形図といいます。早速この樹形図を作っていきましょう。
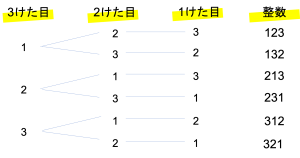
まずは1番目,つまりは3けた目にどのカードが来るのか,ということを考えていきます。出来上がる3けたの整数は,どのけたにどのカードを置くかで変わってきますね。今回3けた目に置かれる可能性があるカードは1か2か3ですね。したがって一番左の列に1・2・3を書き込みましょう。
次に2けた目に置かれる可能性のあるカードを考えます。例えば3けた目に1がきたとき,残っているカードは2と3ですね。よってこのとき2に分かれる枝と3に分かれる枝を書くことができます。同じように1けた目が2のとき・3のときも,それぞれ1と3,また1と2というカードが残っているため,21・23・31・32という4つの枝が書けますね。
このように順番を重ねることで場合の数が増えていくことを視覚的に理解しやすくなるのが樹形図の特徴です。2けた目までで6つの選択肢が現れたので,1けた目の列を埋めて樹形図を完成させましょう。3けた目・2けた目に12がきたとき,残っているカードは3のみになります。したがって必然的に1けた目は3になり,123という整数が表れます。
これと同じように他の13・21・23・31・32というカードの並びでも,必然的に1けた目は残った1まいになるので,選択肢はこれ以上増えず,整数の種類は6通りになります。
A. 6通り
確率の問題を解いてみよう①
では同じ問題を使って,今回は確率の問題を解いていきましょう。
{1,2,3}の3まいのカードをランダムに並べて,3けたの整数を作ります。このとき132という整数が出来上がる確率はどれくらいですか。
このような確率の問題も基本となるのは樹形図です。確率の問題が表れたら,まずは上の場合の数の問題と同じように,出来上がる数字の並びを順番に並べていきましょう。今回であれば6通りの3けたの整数が出来上がりますね。
こうして樹形図を書き上げたら,その後は条件を満たすものに印をつけていきます。本問題では132という整数が出来上がる確率が問われているので,132という数字が目立つよう,下の図のように印をつけていきます。
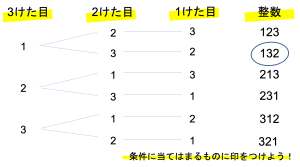
では確率を計算していきます。上の確率の定義で見たように,確率を計算するには全体の場合の数と特定の事柄が起こりうる場合の数とが必要です。この問題で出来上がる整数は6通りなので,分母には6がきます。一方今回の条件を満たす132は出来上がる6つの整数の中でただ1つしか存在しないため,分子には1がきます。よって答えは\(\frac{1}{6}\)となります。
A. \(\frac{1}{6}\)
確率の問題を解いてみよう②
次も同じ問題を使って,確率の計算をしていきましょう。
{1,2,3}の3まいのカードをランダムに並べて,3けたの整数を作ります。このとき出来上がる整数が偶数になる確率はどれくらいですか。
それでは計算していきましょう。このような問題も基本はやはり樹形図です。今回は,既に出来上がる整数がわかっていますが,どのような問題でも樹形図を作ることを意識しましょう。この問題で聞かれているのは3けたの整数のうち偶数になるものなので,偶数に印をつけてその数を数えていきます。
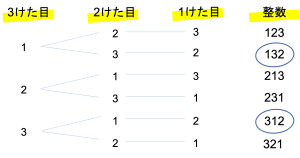
数えた結果,132と312の2つが偶数に当てはまることがわかりました。今回すべての整数が6通り存在するため,整数が偶数になる確率の分母は6,分子は2になります。したがって答えは\(\frac{2}{6}\),約分して\(\frac{1}{3}\)となります。
A. \(\frac{1}{3}\)
樹形図が書きづらいときは?
ではまた別の問題で「並べる」問題の演習をしていきましょう。上の例題と似ていますが,樹形図が使いづらい問題となります。よろしければまずはご自分の力で挑戦してみましょう。
{1,2,3,4,5,6,7,8,9}の9まいのカードの中から3まいを並べて,3けたの整数を作ります。3けたの整数は全部で何通りできますか。
この問題でも,基本に沿って樹形図を作っていきたいところです。しかし上のように樹形図を作るとおそらく各スペースが足りない・いくら書いても書ききれないなんてことになるのではないでしょうか。
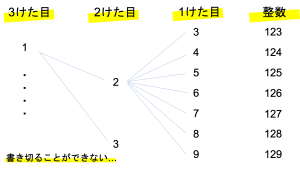
元々のカードの数が多いため,1から9までを全て並べることは難しいです。このような場合は,上の樹形図を簡単にしてかけ算の式に表すことで計算していきましょう。
この問題で3けた目に来るカードは何通りあるでしょうか。今回カードは全部で9まいなので9通りとなります。同じように,2けた目に置かれるカードのまい数と1けた目に置かれるカードのまい数を考えましょう。3けた目にどのカードが来ても,全部のカードの中から1まいだけ使えなくなることは変わりません。したがって2けた目に置かれるカードは3けた目で使われなかった8まいのどれかだとわかります。同様に1けた目に置かれるカードも,3けた目・2けた目で使われなかった7まいのどれかだとわかります。
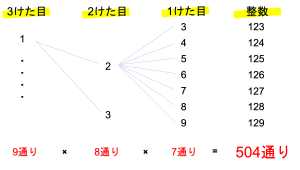
このことから樹形図を書かなくても,3けた目の9通りの数字から8通りの枝が伸び,その9×8本の枝の末端から7通りの枝が伸びているため,9×8×7という式で簡単に表すことがわかります。選択肢の数をかけ合わせることで場合の数は簡単に求めることができるので,樹形図が書きづらいときはこのテクニックを使ってみましょう。
A. 504通り
まとめ
本記事では場合の数と確率という単元についての基礎的な事項をおさらいしていくものでした。応用問題や演習問題を通して場合の数・確率に関する実力をつけたい!という方に向けた発展編の記事もご用意しているので,以下のリンクから飛んでみてください。本記事が学習の手助けになれば幸いです。

















