皆さんは、「圧力」の入試問題に対してどのような印象をもっているでしょうか? 中学受験理科の基礎を勉強している人にとっては、「集中的に勉強したことがないから自信がない」かもしれません。また過去問を解き始めている人からすると、「あまり問題を見かけたことがない」と思うかもしれません。実際、圧力の問題は中学受験理科で必須の分野とは言えません。
しかし、特に「大気圧」などの分野に関して、出題例が少なからずあります。圧力の分野を勉強していなかったことによって、入試本番であせってしまう……ということがないように、まずは幅広い分野の基礎問題を一通り解けるようにした方がよいでしょう。
今回は、実際に出題された「圧力」の入試問題を解説していきます! 後半では、大気圧の測定で有名な「トリチェリの実験」を題材にした問題も解説します。
圧力に関して全く知識がないという人は以下の記事を参考にしてください!
とはいっても、圧力の分野を完ぺきにしてからでないと入試問題を解いていけないわけではありません。問題を解きながら知識を定着させることはとても重要なので、一通り基礎知識を勉強したら問題にチャレンジしてみてください!
それでは解説に入ります。
広島学院中学校 2014年 改題
問題
閉じこめられた空気の力について後の問いに答えなさい。
(1) 図1のようにゴムで先たんを閉じた注射器を用意し、空気を閉じこめて縦に置きました。ピストンを下向きに押しながら空気の体積を小さくしていき、その後ゆっくり元の体積までもどしました。このとき感じる手ごたえはどのようになりますか。

(ア) 体積を小さくしていくにつれて大きくなり、元の体積にもどしていくにつれて小さくなる。
(イ) 体積を小さくしていくにつれて大きくなり、元の体積にもどしていっても変わらない。
(ウ) 体積を小さくしていくにつれて小さくなり、元の体積にもどしていくにつれて大きくなる。
(エ) 体積を小さくしていくにつれて小さくなり、元の体積にもどしていっても変わらない。
(オ) 体積を小さくしていっても、元の体積にもどしていっても変わらない。
(1) 解答
この問題は、空気を圧縮するとどうなるかという基本的な実験的事実を確認しています。
ピストンの中の空気(気体)の圧力と体積の関係は、反比例の関係にあります(中学ではこのことを「ボイルの法則」として習います)。
つまり、気体の体積を小さくすると、圧力は大きくなり、気体の体積を大きくすると、圧力は小さくなるため、答えは
(ア) 体積を小さくしていくにつれて大きくなり、元の体積にもどしていくにつれて小さくなる。
となります。なぜこうなるかを考えてみましょう。
空気はある圧力で、ピストンを押しています。これは、空気の中の粒子がピストンの面にぶつかっているからです。以下の図では簡単のためにピストンにぶつかっている粒子だけを描いていますが、本当はすべての方向に粒子は移動しています。ピストンに力を加えていないとき、粒子がピストンを押す力の総和は大気圧と同じになっています。
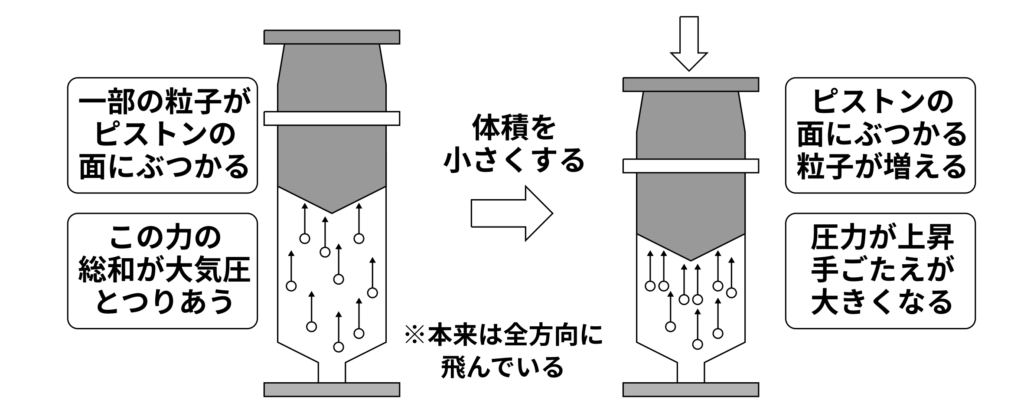
空気の体積が小さくなるとどうなるでしょうか。ピストンの面の大きさは変わっていません。また、空気の体積は減っていますが、注射器は密閉されているので、粒子の数も減っていません。すると、より多くの粒子がピストンの面にぶつかることになります。
結果的に、ピストンにかかる圧力は大きくなり、それを押すために必要な力(=手ごたえ)も大きくなるというわけです。
空気の体積を大きくすると、いま述べたことと逆のことが起こり、圧力は小さくなります。
(2) 注射器に水を入れ、空気が入らないように閉じこめました。(1)と同じようにこれを縦に置き、ピストンを下向きに押しました。このとき水の体積や感じる手ごたえはどのようになりますか。
(ア) 押す力を大きくすると水の体積は小さくなり、手ごたえは大きくなる。
(イ) 押す力を大きくすると水の体積は小さくなり、手ごたえは変わらない。
(ウ) 押す力を大きくしても水の体積は変わらず、手ごたえは大きくなる。
(エ) 押す力を大きくしても水の体積は変わらず、手ごたえも変わらない。
(2) 解答
この問題は、実験をしたことがある人なら簡単にわかるかもしれません。
先ほどの問題では、ピストンを押すと空気の体積が小さくなることが前提でした。
この問題では、「そもそも水をピストンで押すと体積は変わるのか」が問われています。
結論をいうと、水の体積は、圧力を加えても(ほとんど)変わりません。ですが、ピストンの面を押す力は大きくなっているので、水は同じ大きさでピストンを押し返し(作用・反作用の法則)、手ごたえは大きくなります。したがって答えは
(ウ) 押す力を大きくしても水の体積は変わらず、手ごたえは大きくなる。
となります。
なぜ、水の体積は押しても変化しないのでしょうか。
空気と水は下の図のような違いがあります。空気は体積に対して粒子の数が少ないです。そのため、空気に力をかけると簡単に圧縮されます。
一方で、水は体積に対して粒子が密につまっています。そのため、水に力をかけても、粒子が移動するスペースがなく、圧縮されません。
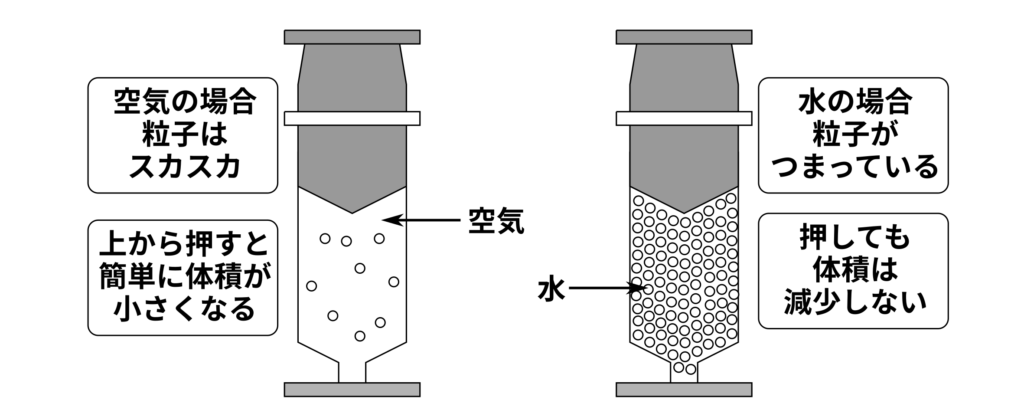
実際、大気圧と同じ力をピストンにかけたとしても、水の体積はもとの0.004%しか変化しません。したがって、水の体積は変化しないと言ってよいでしょう。
また、手ごたえが大きくなるというのは理解できるでしょうか。これは、固体の場合と同じように考えればよいです。
例えば机に指で力を押したとき、力をかければかけるほど、指にかかる力も大きくなることがわかると思います。
これは、机にかけた力と同じだけの力で、机も指を押しているからです。このとき、机の大きさ(体積)は変化してないですよね。
水の場合も同じで、力をかければかけるほど、同じ力の大きさで押し返してきます。
(3) 図2のようにゴムで先たんを閉じた注射器に水と空気を同じ体積ずつ入れて縦に置き、(1)と同じようにピストンを下向きに押しました。このときの様子はどのようになりますか。
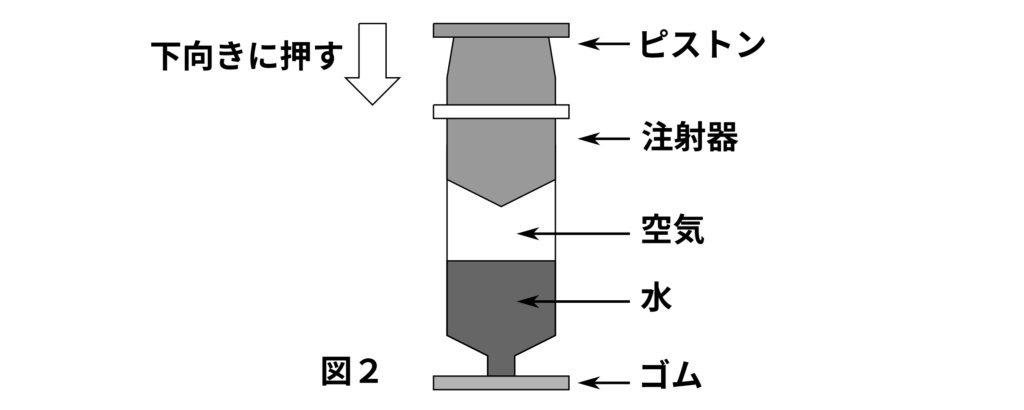
(ア) 空気の体積だけが小さくなる。
(イ) 水の体積だけが小さくなる。
(ウ) 空気の体積も水の体積も小さくなる。
(エ) 空気の体積も水の体積も変わらない。
(3) 解答
この問題は、力の伝わり方を理解したうえで、(1)、(2)をふまえれば答えがわかります。
ピストンに対して下向きにかけた力は、(1)のように、空気の体積を小さくします。このとき、空気も、水に対してピストンから受けたのと同じだけの圧力を水に加えます。
しかし、(2)で見たように、水に力をかけても体積は変わりません。よって答えは
(ア) 空気の体積だけが小さくなる。
となります。
問題にはなっていないですが、注意しておくべき点があります。補足となるので、読み飛ばしてもらっても構いません。
(1)では空気が圧縮されるにつれて、手ごたえも大きくなりました。ですが、空気と水が存在している場合、必ずしも手ごたえが大きくなるとは限りません。
それはなぜかというと、空気中の水蒸気(粒子)が、水の中に溶けるからです。
(1)では、体積が小さくなるにつれてピストンの面を押す粒子の数が増えると説明しましたが、水がある場合、数が増えるはずの粒子は水に入り込むため、その数が変わりません。気体の種類にもよりますが、(1)と同じように圧力があがるわけではないのです。覚えておくと、もしかしたら役に立つかもしれません。
(4) 図3のようにゴムで先たんを閉じた注射器に水を同じ体積ずつ入れ、横にして壁に付けて置きました。ピストンを左向きに押したときの様子は(ア)~(カ)のどれになりますか。

(4) 解答
この問題は、(3)と圧力の伝わり方を使って解くことができます。
まず、水と空気の体積がどうなるかを考えましょう。
水と空気が混ざっているときのそれぞれの体積変化は(3)であつかいました。その結果から、
空気の体積は減って、水の体積は変わらない
と考えることができます。(ア)は水も空気も体積が変化していません。(オ)、(カ)は水と空気両方の体積が減っています。
よって、答えは(イ)、(ウ)、(エ)に絞られました。
次に、圧力の伝わり方について考えます。ここで、パスカルの原理を復習しましょう。
パスカルの原理
水や気体が容器の中に閉じこめられているとき、水や気体に伝わる力はすべての地点、方向で同じになる
パスカルの原理をふまえると、ピストンを左向きに押したからといって、「どこか一部分だけに力がかかるわけではない」ということがわかります。
それぞれの図を詳しく見てみましょう。
(ウ)は左側に水が寄っています。水は自身の重力によって、深さが深い方が多くの圧力を面に加えます。シリンダーに穴をあけたとき、深いところに穴を開けた方が、水が勢いよく飛び出すという実験を知っている人も多いかもしれません。
一方で、パスカルの原理を考えると、空気は水を同じ圧力で押します。空気も深さによって圧力の大きさに違いがありますが、水と比べてかなり小さいため、無視します。すると、水と空気の間に働く圧力は、水の深さが深い地点では右向きに、浅い地点では左向きにかかることになります。力がつりあっていないので、深い場所の水が空気の方に移動し、浅い場所の空気が水の方に移動します。したがって、(ウ)の状況はあり得ません。
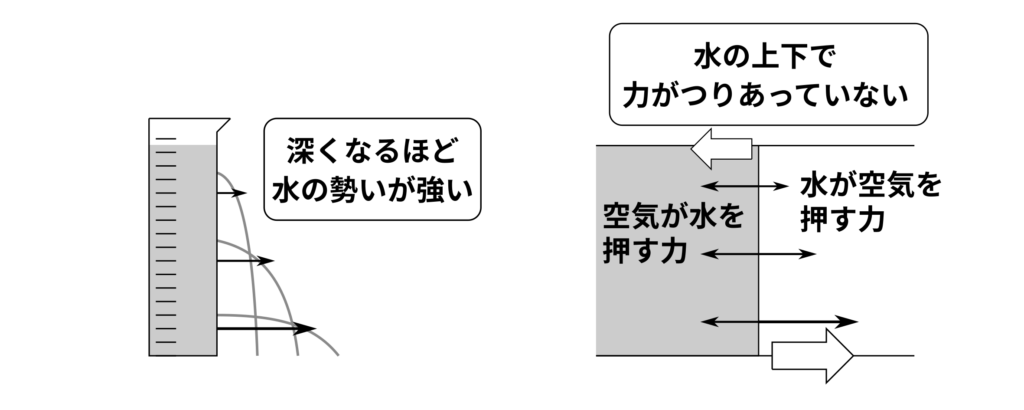
(エ)に関しても同じようなことが言えます。同じ深さで考えた場合、水が斜めになっている右側の部分は、水自身の重さによる圧力が小さく、反対に左側は水自身の重さによる圧力が大きいため水は、右側に流れようとします。この右側に流れる力を、違う深さで考えた場合、深い方が力が大きく、浅い方が力が小さいため、空気が水を押す圧力とつりあうことはありません。結果的に空気の層が上になり、水の層が下になるまで移動を続けます。
よって、答えは力がつりあっている
(イ)
となります。
渋谷教育学園幕張中学校 2017年 改題
問題
水が入ったメスシリンダーを水そうの上で立てると、水そうの液面よりもメスシリンダー内の液面の方が高いのに、メスシリンダー内の水が落ちてこないようにすることができます。
このことに関して、次のことがわかっています。
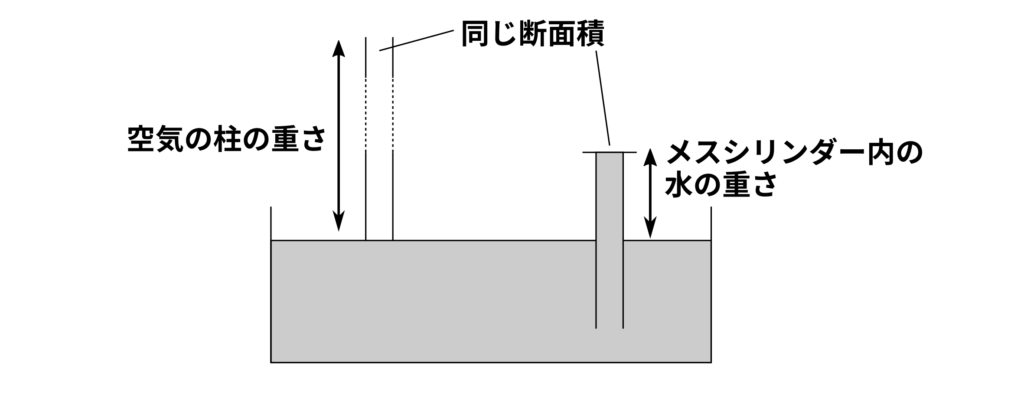
図のように、メスシリンダーの断面積と同じ断面積の空気の柱が、水そうの水面を押している。
空気の柱の重さがメスシリンダー内の水の重さよりも大きいから、水が落ちてこない。
つまり、水そうの上にある空気の柱の重さが、メスシリンダー内の水の重さを支えている。
空気の柱の重さで支えることができる水の重さの限度を調べます。
空気は地上50km~55kmまで分布していますが、上空に行くほど薄くなることが知られています。もし、空気が地上と同じ濃さで均等に分布しているとすると、およそ8km まで空気が存在していることになります。このとき、空気は何 m分の水の重さを支えることができるかを考えます。
(1) 空気は何 m分の重さを支えることができますか。小数第1位まで答えなさい。ただし、\(1\,\mathrm{m^3}\)あたりの空気の重さは\(1.29\,\mathrm{kg}\)とし、\(1\,\mathrm{m^3}\)あたりの水の重さは\(1000\,\mathrm{kg}\)とします。
(1) 解答
問題文の意図をくみとることができたでしょうか? 空気は非常に軽いので、箱に入った空気の重さなどは通常考慮されることはありませんが、大気は地上からはるか遠くにまで達しているため、その影響を無視することができません。
この問題で問われているのは、上空に積み重なる空気と同じ重さの水は、同じ面積あたり、どれくらいの高さまで達するでしょうかということです。
つまり、ある面積当たりにかかる空気の重さを計算したあと、それと同じだけの重さの水がどれくらいの体積になるかを計算し、それを断面積で割ればよいのです。
まず、空気の重さを考えましょう。空気は本来50km~55kmまで分布していますが、高さによって密度が違うので、重さを計算するのが難しいです。ここでは問題を簡単にするために、密度が同じで、8kmの高さまで分布する大気を考えます。
例えば、断面積を\(1\,\mathrm{m^2}\)とすると、その重さは、
\(8000\,\mathrm{m} \times 1.29\,\mathrm{kg\,/\,m^2} \times 1\mathrm{m^2} = 10320\,\mathrm{kg}\)
となります。次に、断面積が\(1\,\mathrm{m^2}\)の柱を考えると、同じ重さの水は
\(10320\,\mathrm{kg} \div 1000 \mathrm{\,kg\,/\,m^2} \div 1\,\mathrm{m^2} = 10.32\,\mathrm{m}\)
となります。答えは小数第1位までなので、答えは
\(10.3\,\mathrm{m}\)
と求めることができます。
ここで、断面積の大きさは自由に決めてよいというのがこの計算の特徴です。つまり、圧力を計算しているので、単位面積当たりの力のみが重要であり、シリンダーなどの断面積の大きさによらず、水の高さは\(10.3\,\mathrm{m}\)になるということです。
(2) 水で空気の柱の重さをはかる場合には、かなり大がかりな装置を作らなければいけません。そこで、400年ほど昔に水銀という液体を使った装置が使用され始めました。水銀を使うと、80 cmほどの高さで装置を作ることができます。
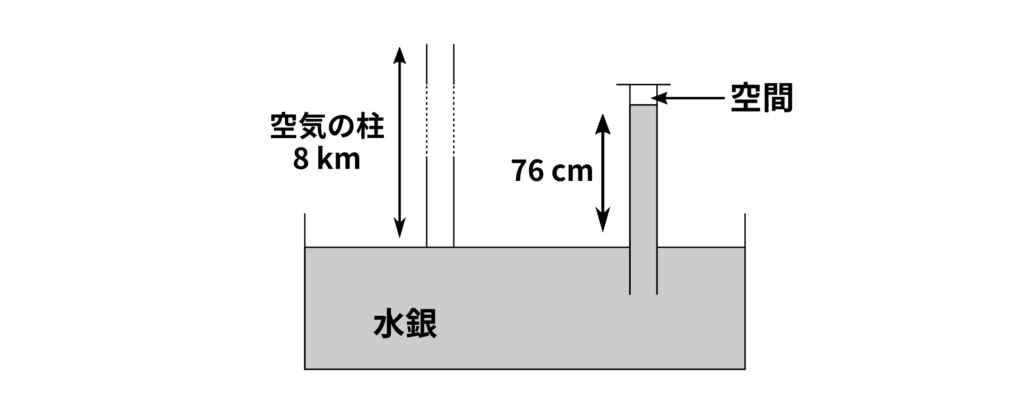
断面積\(2\,\mathrm{cm^2}\)の管で図のような装置を作ります。(1)の空気とつり合う水銀の柱の高さが\(76\,\mathrm{cm}\)であるとき、水銀\(1\,\mathrm{cm^3}\)あたりの重さは何\(\,\mathrm{g}\)ですか。小数第1位まで答えなさい。
(2) 解答
この実験はトリチェリの実験といって、非常に有名です。もとは大気圧を測定するためにあみ出された手法です。
水銀は、水に比べて密度の大きい液体です。そのため、水よりも少ない体積で、大気圧とつり合うことができます。
解答の方針を考えます。まず、問題文では断面積が\(2\,\mathrm{cm^2}\)とありますが、先ほどの解説で述べた通り、断面積の大きさは関係がありません。なので、簡単に\(1\,\mathrm{cm^2}\)としましょう。
大気の重さは先ほどの問題の結果を使えばよいです。ただし、断面積が違うので注意が必要です。\(1\,\mathrm{m^2}\)あたりの大気の柱の重さは
\(10320\,\mathrm{kg}\)
でした。ここで、\(1\,\mathrm{cm^2}\)は\(1\,\mathrm{m^2}\)に比べて\(1/10000\)の大きさなので、\(1\,\mathrm{cm^2}\)あたりの大気圧の重さは
\(1.032\,\mathrm{kg}\)
となります。次に、水銀の\(1\,\mathrm{cm^3}\)あたりの重さは、この重さを柱の体積で割れば出てきます。したがって、
\(1.032\,\mathrm{kg} \div (76\,\mathrm{cm}\times 1\,\mathrm{cm^2}) = 0.01357\,\mathrm{kg} \)
となります。求めるのは\(\,\mathrm{g}\)であり、小数第1位までの計算なので、
\(13.6\,\mathrm{g}\)
と求めることができます。
最後に
本記事では、「圧力」に関する入試問題の解説をおこないました! 内部に水と空気が両方はいっている注射器を圧縮する問題、トリチェリの実験を題材にした問題、いずれも圧力に関する基本的な事柄を理解していないと解答は難しいと思います。ですが、逆に言えば、基本さえマスターしておけば、あとは入試本番で対応できる程度の問題しか出題されないともいえます。パスカルの原理や、大気圧の影響など、圧力の基礎を理解する重要性を身に染みたのではないでしょうか? それでは引き続き、中学受験理科の勉強を頑張ってください!
おすすめ記事
- 圧力 ~圧力の計算式は何? 圧力、気圧、水圧の基礎を確認し、問題を解いて理解しよう~【中学受験理科】
- 圧力 ~パスカルの原理とは何? 圧力の伝わり方を基礎から理解しよう!~【中学受験理科】
- 中学受験・理科 浮力が苦手な人必見!点数をとる方法は?
- 物理の勉強法~苦手な人への処方箋
- 【中学受験】今だからできる!理科勉強法・克服法 物理編