皆さんは中学受験の理科の問題と聞いて何を思い浮かべるでしょうか? 植物、天体、水溶液など様々な分野がありますが、ばねの問題を思い出す人は少ないのではないでしょうか。
それもそのはずで、ばねの問題は必ずしも入試で頻出というわけではありません。しかし、ばねの問題としては超基礎的な知識も、身につけていなければ入試本番で大きな差をつけられてしまう確率が高いです。
今回は、必ず知っていてほしいばねの典型的な知識について解説します。特に、ばねにおける直列と並列の概念について説明しますので、現時点であやふやだという人は最後の応用問題まで解いてみてください! それでは早速解説します。
ばねの超基本
まず、ばねの基礎知識について復習しましょう。一般に、「ばねの長さ」といったとき、次の式が成り立ちます。
ばねの長さ\(=\)ばねの自然長\(+\)ばねの伸びた長さ
あるいは
ばねの長さ\(=\)ばねの自然長\(–\)ばねが縮んだ長さ
ここで、「自然長」とは「ばねを伸び縮みさせる前の長さ」です。「ばねに力がかかっていないときの長さ」とも言いかえることもできます。
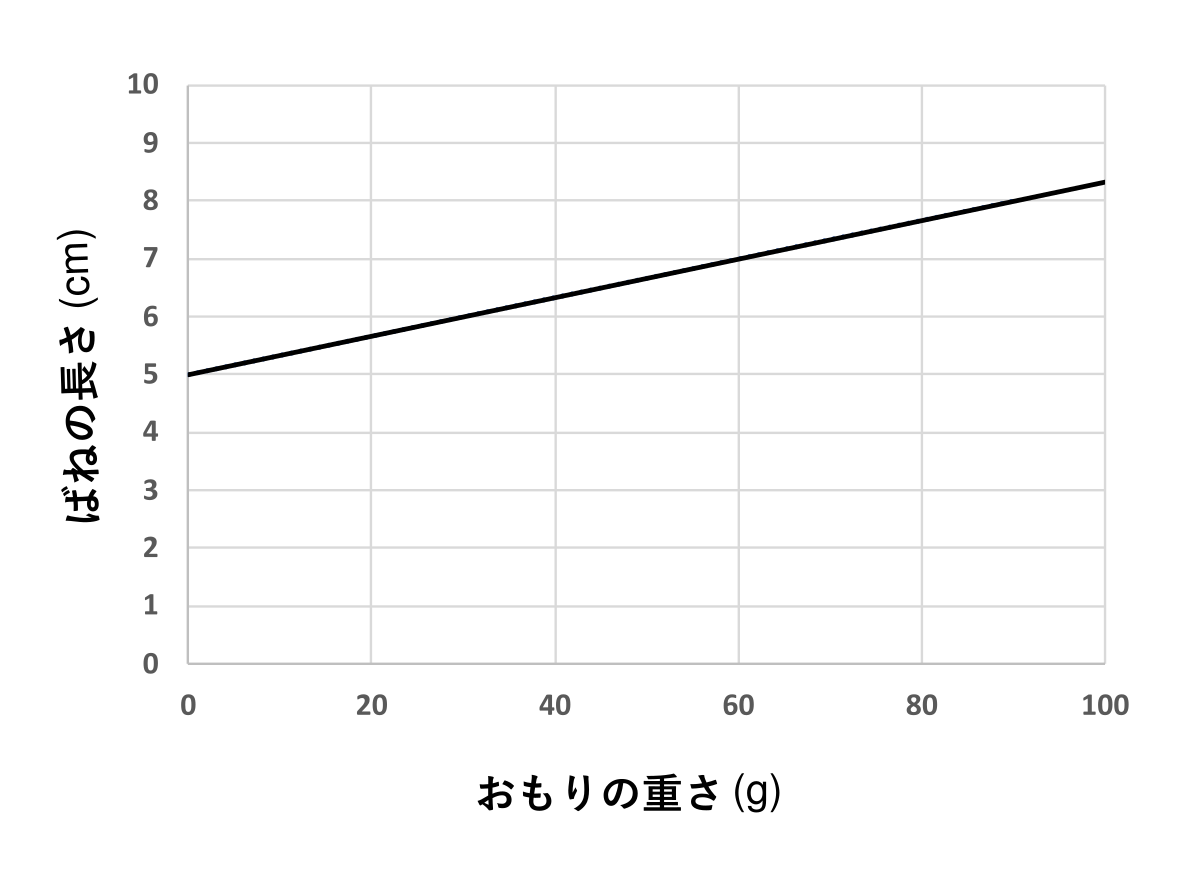
さらに基本的なこととして、「ばねの伸び」はばねにかかる力に比例します。例えば次のようなグラフが与えられたとき、「自然長」は\(5\,\mathrm{cm}\)で、ばねの伸びは、おもりの重さ\(15\,\mathrm{g}\)につき\(1\,\mathrm{cm}\)です。
ばねの基本については以下の記事でより詳しく解説しているので、これまでの説明でつまづいたという人は参考にしてください!
ばねの直列つなぎ
では、これからばねの問題について少しづつ内容を掘り下げていきましょう。電流の知識がある人には理解しやすいかもしれませんが、ばねは「直列」につないだときと、「並列」につないだときで、力のかかり方が変化します。まずは「直列」につないだときです。
次の問題を解きながら理解していきましょう。
以下の図のように、天井からばねがぶら下がっている。このばねはすべて同じ種類であり、おもり\(10\,\mathrm{g}\)あたり\(1\,\mathrm{cm}\)だけ伸びる。ばねの重さは考えないものとする。
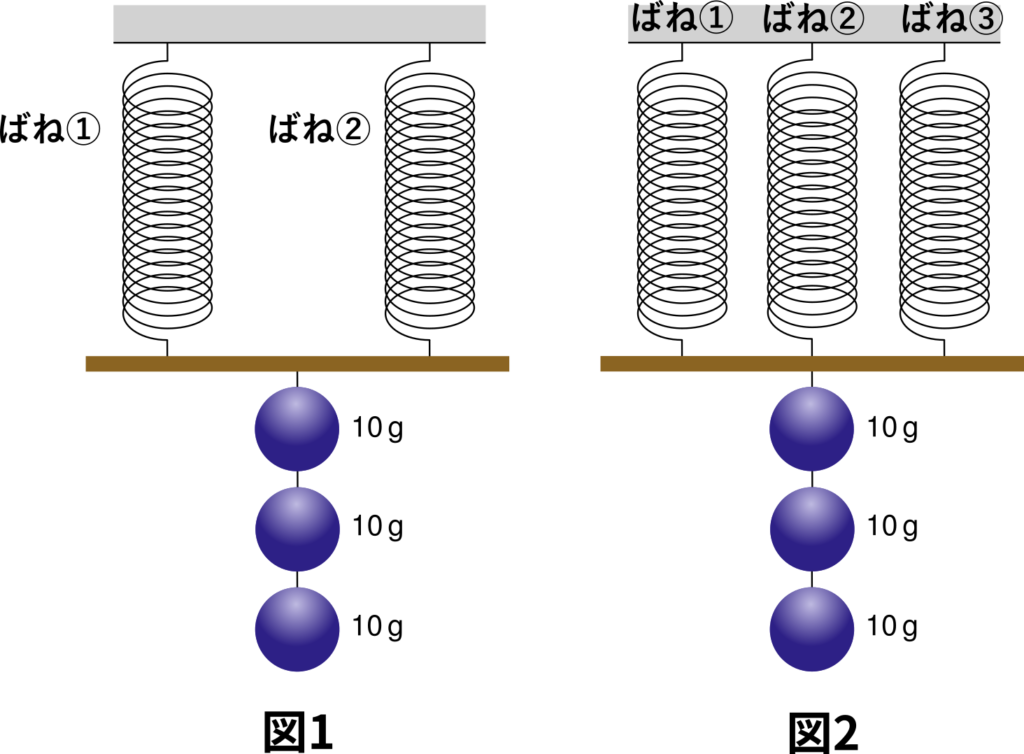
問1 図1のように、2つのばね①と②が直列につながっている場合を考える。おもりの重さは1つ\(10\,\mathrm{g}\)である。このとき2つのばね①と②はそれぞれ何\(\,\mathrm{cm}\)だけ伸びるでしょうか。
問2 図2のように、2つのばね①と②が直列につながっていて、間におもりがある場合を考える。おもりの重さは1つ\(10\,\mathrm{g}\)である。このとき2つのばね①と②はそれぞれ何\(\,\mathrm{cm}\)だけ伸びるでしょうか。

解説
問1
ばねを直列につないだときの考え方は簡単です。直列につないだときのばねの伸びは「そのばねより下にあるばねの重さの合計」に比例します。これより、それぞれのばねの下にあるおもりの重さを考えると、
ばね① … \(10\,\mathrm{g}\times 2 = 20\,\mathrm{g}\)
ばね② … \(10\,\mathrm{g}\times 2 = 20\,\mathrm{g}\)
よってどちらも\(20\,\mathrm{g}\)の重さがかかるので、ばねの伸びはどちらも
\(20\,\mathrm{g}\div 10\,\mathrm{g}\times 1\,\mathrm{cm} = 2\,\mathrm{cm}\)となります。
気づいた人がいるかもしれませんが、1つのばねが天井からぶら下がっている場合でも、ばねの伸びが「そのばねより下にあるばねの重さの合計」に比例することは成り立ちます。ばねが1つの場合と同じように考えることができるので、答えを求めるのはそこまで難しくないでしょう。
問2
先ほどよりも若干複雑になりましたが、考え方は同じです。それぞれのばねの下にあるおもりの重さを考えてみましょう。
ばね① … \(10\,\mathrm{g}\times 2 = 20\,\mathrm{g}\)
ばね② … \(10\,\mathrm{g}\times 1 = 10\,\mathrm{g}\)
この問題では、ばね①とばね②の間に違いができました。これは、ばねとばねの間にあるおもりがばね①にとっては下にありますが、ばね②にとっては上にあるからです。したがって、ばね②にかかるおもりの重さ少なくなります。したがって、ばねの伸びはそれぞれ
ばね① … \(20\,\mathrm{g}\div 10\,\mathrm{g}\times 1\,\mathrm{cm} = 2\,\mathrm{cm}\)
ばね② … \(10\,\mathrm{g}\div 10\,\mathrm{g}\times 1\,\mathrm{cm} = 1\,\mathrm{cm}\)
と求めることができます。
ばねの並列つなぎ
次は「並列」につないだ場合です。今回も問題を解きながら理解しましょう。
以下の図のように、ばねが軽い木の棒で並列につながって、天井からぶら下がっている。このとき、木の棒は水平になっている。また、このばねはすべて同じ種類であり、おもり\(10\,\mathrm{g}\)あたり\(1\,\mathrm{cm}\)だけ伸びる。ばねと木の棒の重さは考えないものとする。
問1 図1のように、2つのばね①と②が並列につながっている場合を考える。おもりの重さは1つ\(10\,\mathrm{g}\)である。このとき2つのばね①と②はそれぞれ何\(\,\mathrm{cm}\)だけ伸びるでしょうか。
問2 図2のように、3つのばね①、②、③が直列につながっている場合を考える。おもりの重さは1つ\(10\,\mathrm{g}\)である。このとき3つのばね①、②、③はそれぞれ何\(\,\mathrm{cm}\)だけ伸びるでしょうか。
解説
問1
ばねを並列に2本つないだとき、木の棒が水平を保っているならば(木の棒が水平にならない場合や、ばねの種類が違う場合はてこの考え方を使う必要があります。)、1つのばねのかかるおもりの重さは\(\frac{1}{2}\)になります。これより、それぞれのばねにかかるおもりの重さは
ばね① … \(30\,\mathrm{g}\div 2 = 15\,\mathrm{g}\)
ばね② … \(30\,\mathrm{g}\div 2 = 15\,\mathrm{g}\)
となります。したがって、ばねの伸びはどちらも
\(15\,\mathrm{g}\div 10\,\mathrm{g}\times 1\,\mathrm{cm} = 1.5\,\mathrm{cm}\)と求めることができます。
問2
では、ばねが3つになった場合は、1つのばねにかかるおもりの重さどうなるでしょうか。この場合も木の棒は水平になっています。これは先ほどと同じように\(\frac{1}{3}\)になります。同じように、ばねの数が4つ5つ…と増えた場合には\(\frac{1}{4}\)、\(\frac{1}{5}\)…となります。それぞれのばねにかかるおもりの重さは、
ばね① … \(30\,\mathrm{g}\div 3 = 10\,\mathrm{g}\)
ばね② … \(30\,\mathrm{g}\div 3 = 10\,\mathrm{g}\)
ばね③ … \(30\,\mathrm{g}\div 3 = 10\,\mathrm{g}\)
となります。したがって、ばねの伸びはいずれも
\(10\,\mathrm{g}\div 10\,\mathrm{g}\times 1\,\mathrm{cm} = 1\,\mathrm{cm}\)と求めることができます。
ここまでで、並列の場合は直列とまったく違う力のかかり方をすることがわかったと思います。先程も少しだけ述べましたが、いま解説した並列の考え方は「木の棒が水平であること」、「ばねの種類が同じであること」が重要になります。これに当てはまらない状況のときは「てこ」の考え方が必要になるなど、複雑になるので注意しましょう。
応用問題に挑戦!
では、これまでに解説した知識のみを使った応用問題に挑戦してみましょう。一見複雑に見えますが、一つ一つ分解して考えればきっと解けると思います。
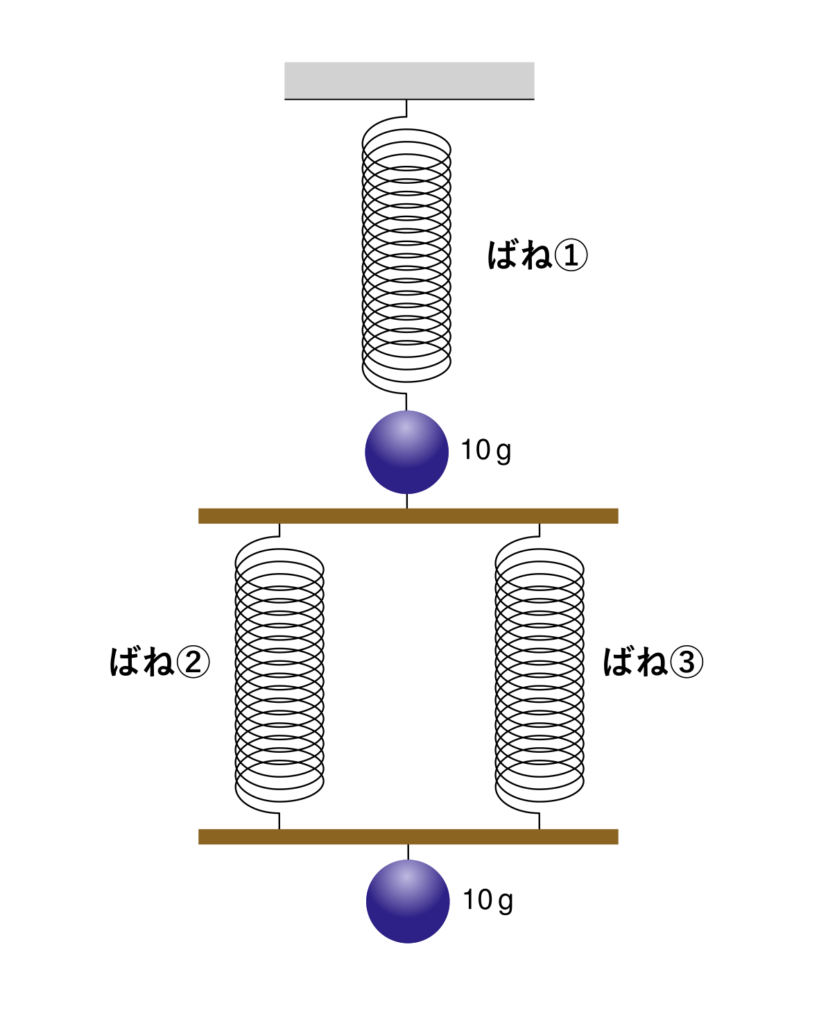
以下の図のように、ばねとおもりが天井からぶら下がっている。このとき、木の棒は水平になっている。また、このばねはすべて同じ種類であり、おもり\(10\,\mathrm{g}\)あたり\(1\,\mathrm{cm}\)だけ伸びる。ばねと木の棒の重さは考えないものとする。ばね①、②、③の伸びはそれぞれ何\(\,\mathrm{cm}\)になるでしょうか。
解答
まず、それぞれのばねにかかるおもりの重さを考えましょう。ばね②と③を見てください。この2つのばねの下にあるおもりは一つだけです。またばね②と③は並列につながっていて、「ばねの種類が同じ」、「棒が水平である」という条件を満たしています。これより、それぞれのばねにかかるおもりの重さは\(\frac{1}{2}\)になります。次に、ばね①を見てください。このばねの下にあるおもりは2つあります。ばねは直列につながっているので、このばねには2つのおもりの重さがかかっています。まとめると、
ばね① … \(10\,\mathrm{g}+10\,\mathrm{g} = 20\,\mathrm{g}\)
ばね② … \(10\,\mathrm{g}\div 2 = 5\,\mathrm{g}\)
ばね③ … \(10\,\mathrm{g}\div 2 = 5\,\mathrm{g}\)
となります。したがって、ばねの伸びはそれぞれ
ばね①の伸び … \(20\,\mathrm{g}\div 10\,\mathrm{g}\times 1\,\mathrm{cm} = 2\,\mathrm{cm}\)
ばね②の伸び … \(5\,\mathrm{g}\div 10\,\mathrm{g}\times 1\,\mathrm{cm} = 0.5\,\mathrm{cm}\)
ばね③の伸び … \(5\,\mathrm{g}\div 10\,\mathrm{g}\times 1\,\mathrm{cm} = 0.5\,\mathrm{cm}\)
と求めることができます。
まとめ……の前に
登録6000人以上!
本サイト、中学受験ナビの監修も務めている『開成番長』こと繁田和貴が執筆する完全無料のメールマガジンでは、主に中学受験生のお子さんをお持ちの方へ向けた様々なお役立ち情報を配信中!
さらに今なら登録者にはもれなく「開成番長・繁田の両親が語る繁田の中学受験PDF」をプレゼント!
登録及び登録解除も簡単ですので、お気軽にご登録ください。

最後に
今回の記事では、ばねの「直列つなぎ」と「並列つなぎ」を解説しました。直列の場合も並列の場合も、下にあるおもりの重さのみに依存します。ですが、それぞれのばねの伸び方は異なります。直列の場合は単純な足し算ですが、並列の場合のばねの伸びは、並列につながっているばねの数に反比例します。このとき、「ばねの種類が同じ」「棒が水平である」という点にも注意すると、今後のばねの学習がスムーズに進みます。最後の問題を解けなかったという人も、もう一度落ち着いて考えれば必ず解けると思いますので、復習がてら再挑戦してみてください!