今回の記事では,平面図形の範囲の1つである図形の折り返し問題に着目するシリーズの3本目として,難関校で出題されるような発展的なレベルの問題の解説を行っていきます。問題の難易度が高いため,与えられる情報量が多く,またそれを活用していくのにも苦戦するでしょう。しかし高いレベルの学校を目指されている方は,ぜひ周りと差をつけるためにお読みいただき,さらなるステップアップを図っていただけますと幸いです。
図形の折り返しとは…?基礎編&応用編振り返り
はじめに基礎編・応用編でお教えした内容を振り返っていきましょう。この2つの記事のうち,まず基礎編では図形の折り返し問題が図形の一部を決まった線で折る問題のことだと紹介した後,その攻略の手段として対応する部分への注目というテクニックをご説明しました。この範囲の問題において図形はあくまで折り返されているに過ぎず,それ以上の変形や移動は行われていません。それゆえ折れ線を境に図形は鏡合わせになっています。このことを活かして情報を埋めていくことの重要さを,基礎編では例題とともに解説しました。
そして応用編ではこのテクニックを用いて受験に登場した問題を解き進めていきました。その中で説明したポイントとしては,文章題の情報を図表に整理しておくことやロスの無いような過程で計算することを取り上げましたね。この応用編では角度についての問題しか引用しませんでしたが,今回引っ張ってきた問題は面積についての内容が問われます。そのため苦戦してしまうかもしれませんが,要領は基本的に同じです。焦らず向き合っていただければと思います。
問題① 円が登場する問題!
それでは各編の振り返りも済んだところで,上で説明した注意点・攻略法などを活かしながら問題を見ていきましょう。今回はそれぞれボリュームがある問題なので2問のみの引用にとどめました,最初は円が登場するものです。文章が長く投げ出したくなってしまうかもしれませんが,ぜひ頑張ってみましょう。
図のように,直角二等辺三角形ABC,長方形ACDEと,DEを直径とする半円が組み合わされた図形があります。ACの長さは8cm,CDの長さは4cmで,長方形ACDEはぬりつぶされています。いま,半円をDEを折り目にして,長方形の上に重なるように内側に折り返します。さらに,直角二等辺三角形ABCをACを折り目にして,折り返した半円の上に重なるように内側に折り返します。このとき,ぬりつぶされた部分のうち,見えている部分の面積を求めなさい。ただし,円周率は3.14とします。
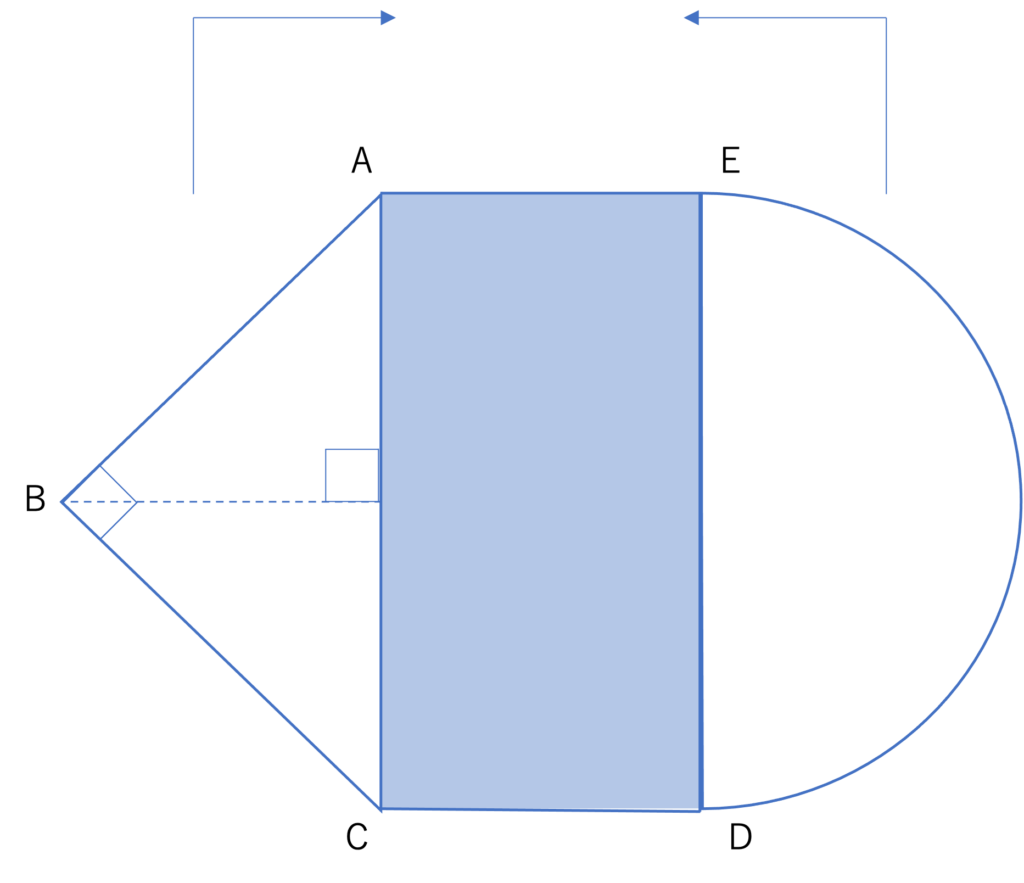
(神奈川学園中学校(2020),一部改題)
解説①
ここからは1問目の解説に移ります。前述したように問題文が長いだけあって,なかなか理解するだけでも時間がかかってしまいそうですね。ただ計算過程で簡単にできる部分はあっても,情報の整理は一切スキップできませんので,着実にシチュエーションをまとめていきましょう。まずこの問題の図形ですが,これは折り返される前のものですが,これだと求める部分の面積が見えにくいですよね。そのため折り返す前の図形が登場する場合,自分で図を描きながら面積を「見える化」していきましょう。この問題ではまず半円の部分を折り返すといわれています。ここでDEは長方形の反対側にある辺であるACと等しく,DEは半円の直径になっているので,半円の直径は8cm・半径は4cmであると分かります。そして長方形の横の長さも4cmであることから,半円を折り返したら端が長方形の端と重なると判断できますね。このことからまず図形は次のように変形すると分かります。
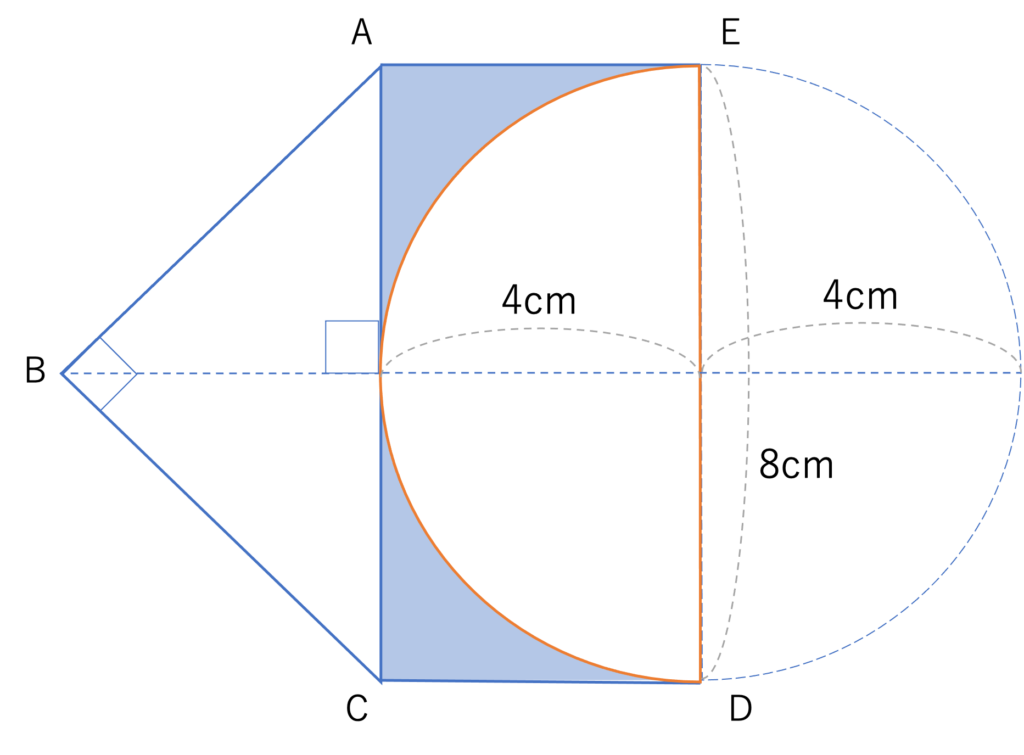
そして問題文では,この次に三角形の部分も折り返すと言われていますね。この指示も図に起こしていきましょう。先の説明では「見える化」という表現をしましたが,図形の問題は特に手を動かしていくことで整理できる情報や,逆に「ここが分かればいいんだけどなあ」といった回答のヒントになりそうな要素が明らかになることが多いです。そこまで丁寧に描く必要はないですが,一つのテクニックとして覚えておきましょう。
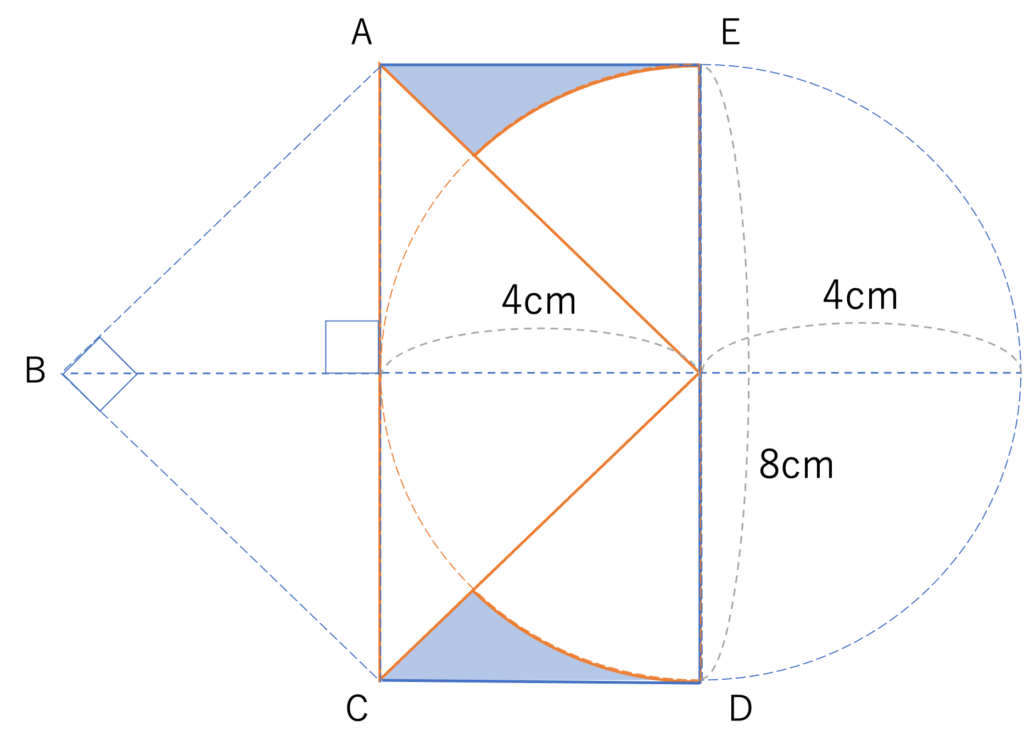
このように操作を図に起こすことで,あんなに長かった文章題がちょっとだけスッキリしますで。要するに,5行も6行もあった文章は上の青い部分の面積を求めなさいという内容にまとめられます。この点で「見える化」の意味を理解していただけますと幸いです。さて,ではここからは青い部分の面積を求めていきましょう。この部分は上と下の2つに分かれています。その片方を見ていき,面積を求めた後に2倍すれば答えとなる2つの部分の合計まで計算できそうです。これが計算のロスをなくすということですね。さてこのとき上の部分に注目しますと,長方形を真ん中の線で半分にした四角形を,これまた対角線で半分にした三角形から扇型を引いた形に見えますね。そのためここからは三角形と扇型の面積について考えてみます。
まず三角形ですが,この図形はAEを底辺・Eから円の中心に向かって伸びる線分,つまり半径を高さとしている,とみなせます。いまAEの長さも半径の長さも4cmであるので,この図形は二等辺三角形であり,面積は4×4÷2=8cm2だと分かります。次に扇型ですが,いま青い部分にまつわる三角形が二等辺三角形であること,およびABCを折り返した図形が二等辺三角形であり半円の半径がその頂角を半分にしていることから,次のような対応関係が確認できます。
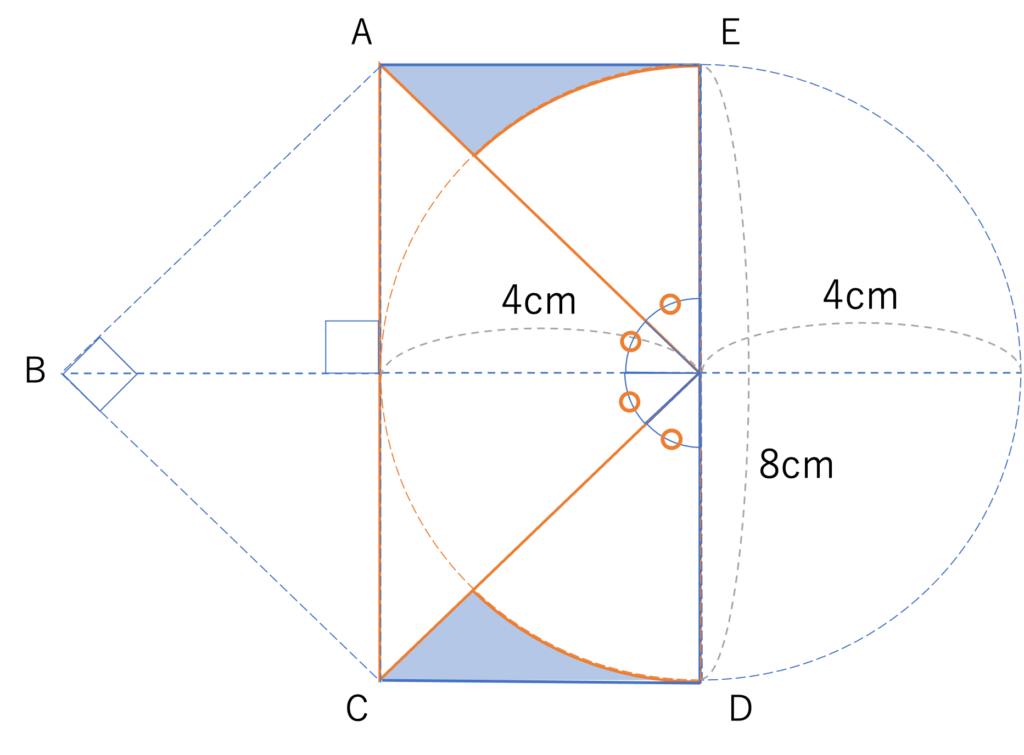
このことから扇型の中心角は180°÷4=45°だと分かります。以上のように,対応関係には随時注目しておくと問題を解くのが楽になりますので,どことどこが一致しそうかな,と頭の片隅で考える癖をつけておきましょう。さてこのことから扇型の面積も求められますね。半径が4cmであることと上の計算を合わせると,面積は4×4×3.14×45°÷360°=6.28cm2になります。なお,以上の過程において4×4×45が360×2と同じになることを抑えておくと計算が一気に簡単になりますので,その部分に注目できているといいですね。
さてあとは引き算により,この上の青い部分の面積は8cm2-6.28 cm2=1.72cm2だと求められますね。いま青い部分は2つあり,今回求めたのはその片方に過ぎません。それゆえその部分を忘れずに値を2倍してあげれば,答えは1.72cm2×2=3.44cm2となります。
A.3.44cm2
このように円が出てきても図が折り返し前でも,丁寧に考えることを続ければ案外簡単な問題になることも折り返し問題では多いです。そのため文章量に怯えず,むしろ文章が多いということはその分ヒントが多い!という意識で解いていただくといいでしょう。
問題② 何回も折り返しが起こる問題!
さて続いての問題は何回も折り返される問題に注目してみます。折り返しが多いと図形も複雑になりますので解答する上で悩みやすいでしょう。ですがこれまでと同じ要領で向き合えば解けるはずです。なお,この問題では内角や外角の性質が登場していることにも注意が必要ですね。もしこれらの考え方を忘れてしまった場合は別の記事で確認してから解いてみてもいいでしょう。
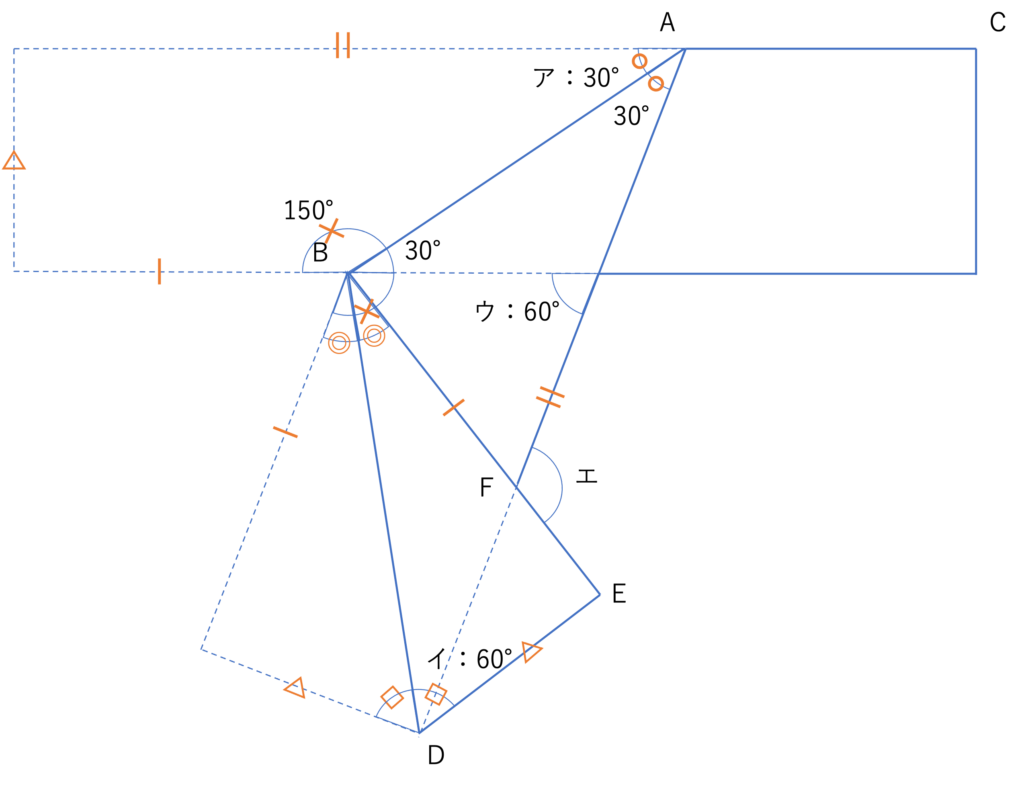
下の図のように,長方形の紙をABを折り目として折り返したあと,BDを折り目として折り返しました。角アは30°,角イは60°,AC=5cm,EF=4cmであるとき,角ウ,エの大きさを求めなさい。
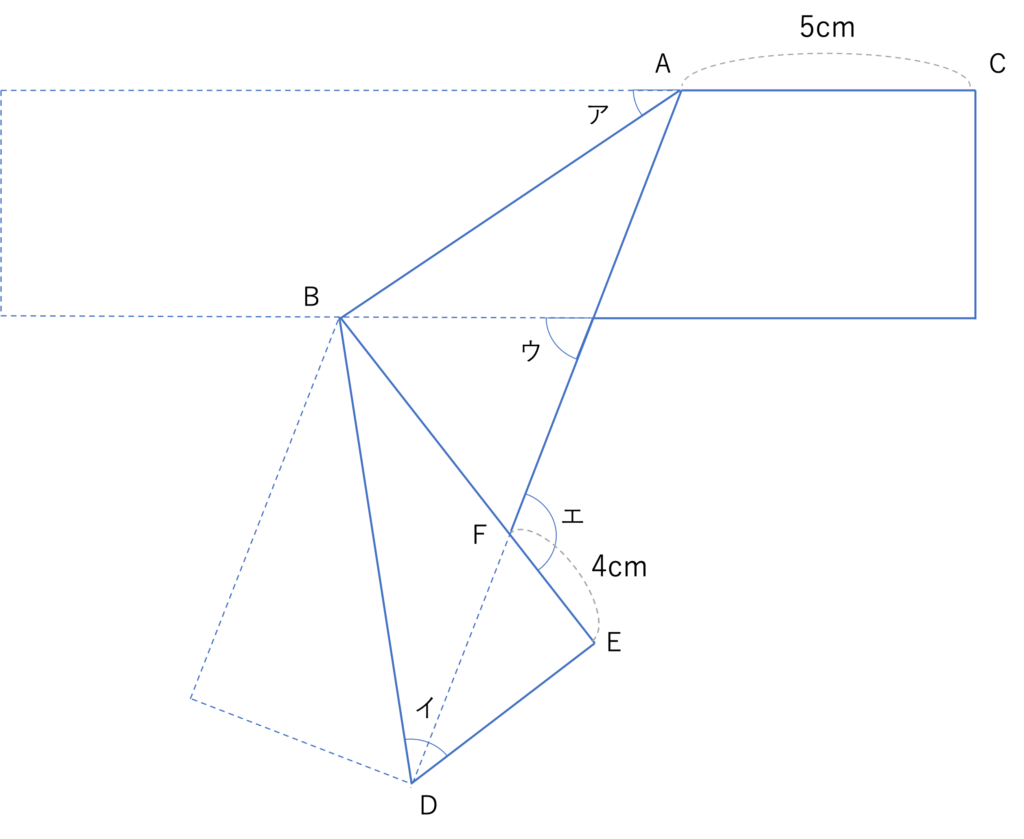
(白百合学園中学校(2021),一部改題)
解説②
それではここからは解説を行っていきます。まず今回の問題を見ると,ウとエの大きさについて求める必要のある角度の問題だと分かります。そのためこの問題も操作こそ複雑ですが,応用編で見た問題と同様の手順で対応関係の確認から進めていけば答えを求められそうですね。ここでは2回の折り返しが行われているので,まずは問題文から分かる情報と1回目のABにおける折り返しによって分かる対応関係を整理してみましょう。
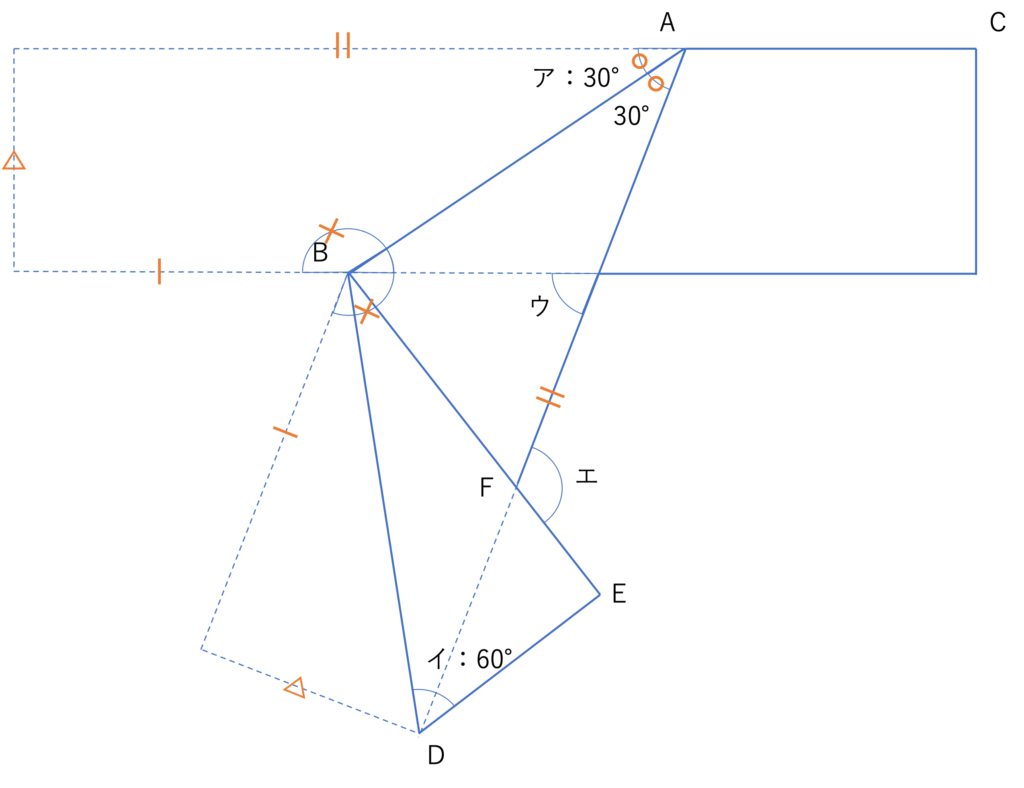
そして続いてこの図をもとに,2回目の折り返しによって分かる対応関係を埋めていきましょう。2回の折り返しをいっぺんにまとめるよりも,それぞれ分けて考えていった方が内容を結びつけやすいです。例えば上の図形では△でマークされている辺が対応していますが,2回目の折り返しによって△の辺はさらに移動しているので,図形中に全部で3つ△に対応する部分があることになるのですが,このような関係性は分割して書き込んでいった方がおそらく見つけやすいのではないでしょうか。慣れてきたらスピードアップを心がけてもいいでしょうが,慣れないうちはゆっくり前提を確認していくといいでしょう。
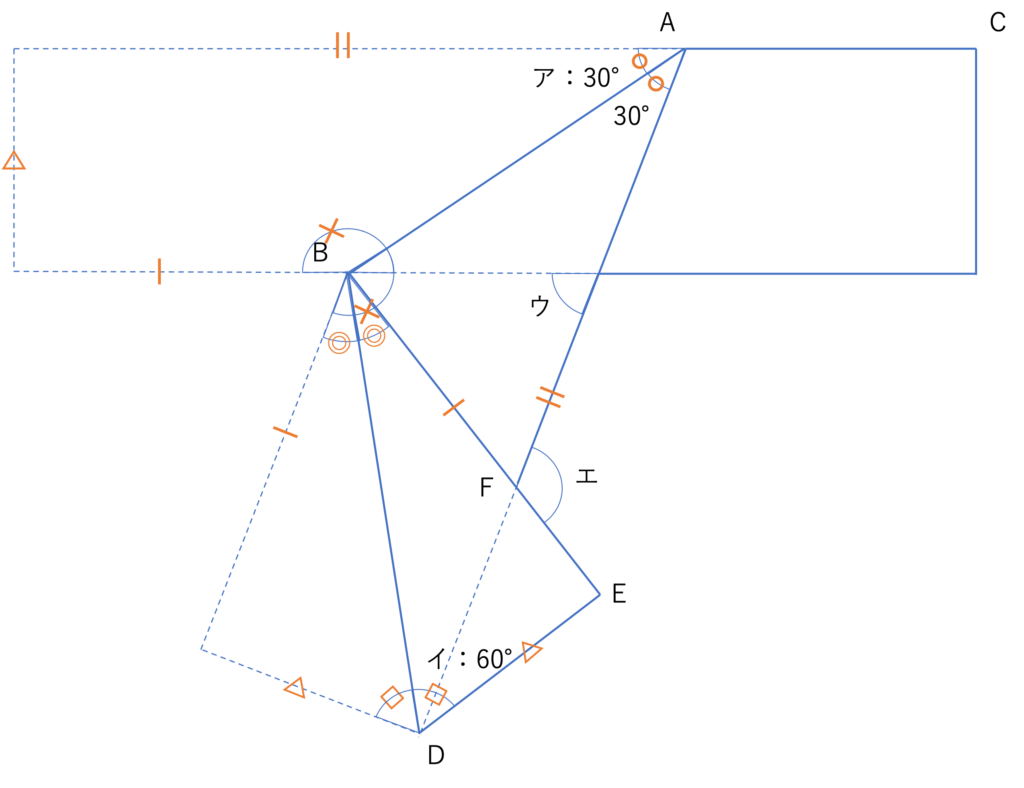
さてここまでが問題文から分かることです。あとはこれらの対応関係をもとにそれぞれの角度を計算していきましょう。この手の問題はアイウエオ順やアルファベット順で答えが求まるようになっているのが一般的ですので,まずはウから見ていきます。この部分はいろいろな見方ができますが,そのうちの一つとして,ウはアを折り返した○で示された角度を含む三角形の外角だとみなせますね。そのため30°・ウの反対側の角以外の角度である,オレンジでマークした角度の大きさが分かれば答えが求められそうです。
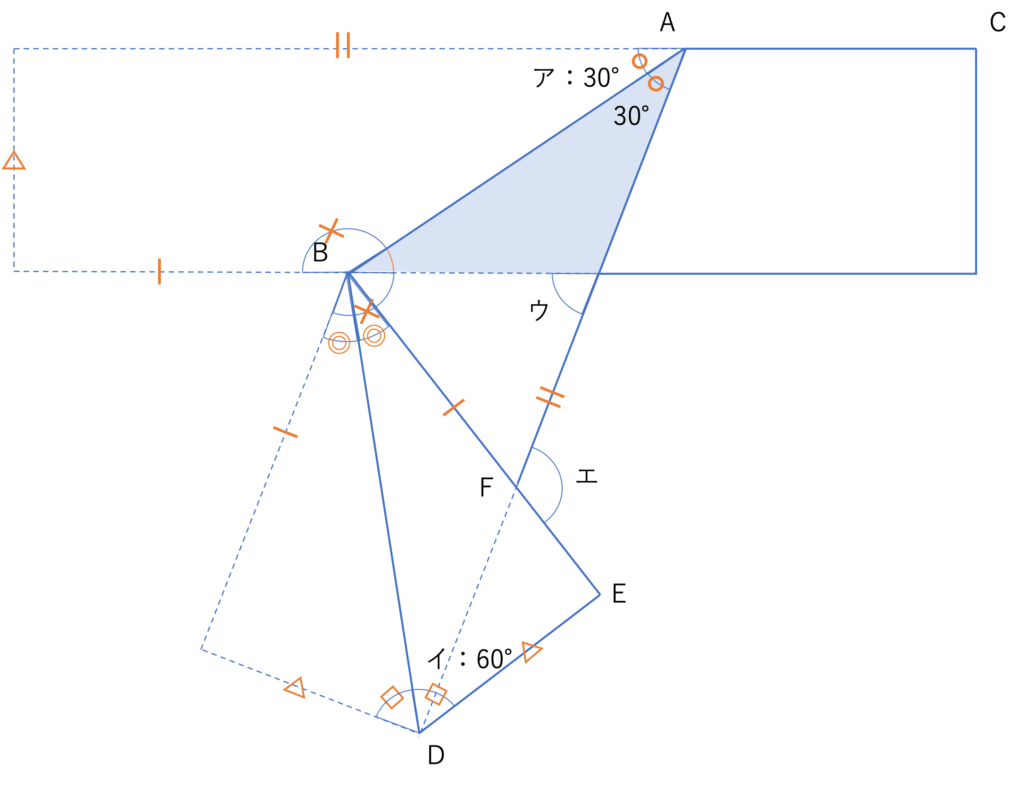
この部分は×で示した角の反対側にあります。そして×の角度は四角形の内角の和の関係から360°-(90°+90°+30°)=150°となりますので,オレンジの部分は30°と分かり,青で示した図形は二等辺三角形だと分かります。このことから二等辺三角形の頂角の外角であるウの大きさは,30°+30°=60°となります。
続いてエの大きさですが,この部分もさまざまな捉え方が可能です。その中でも先ほどのウの大きさを使っていくとしたら,下の図形で塗りつぶしたような三角形における外角だとみなせるでしょう。したがってここからはこの三角形において,ウの角度でもエの反対にある角度でも無い内角の大きさを計算していきます。
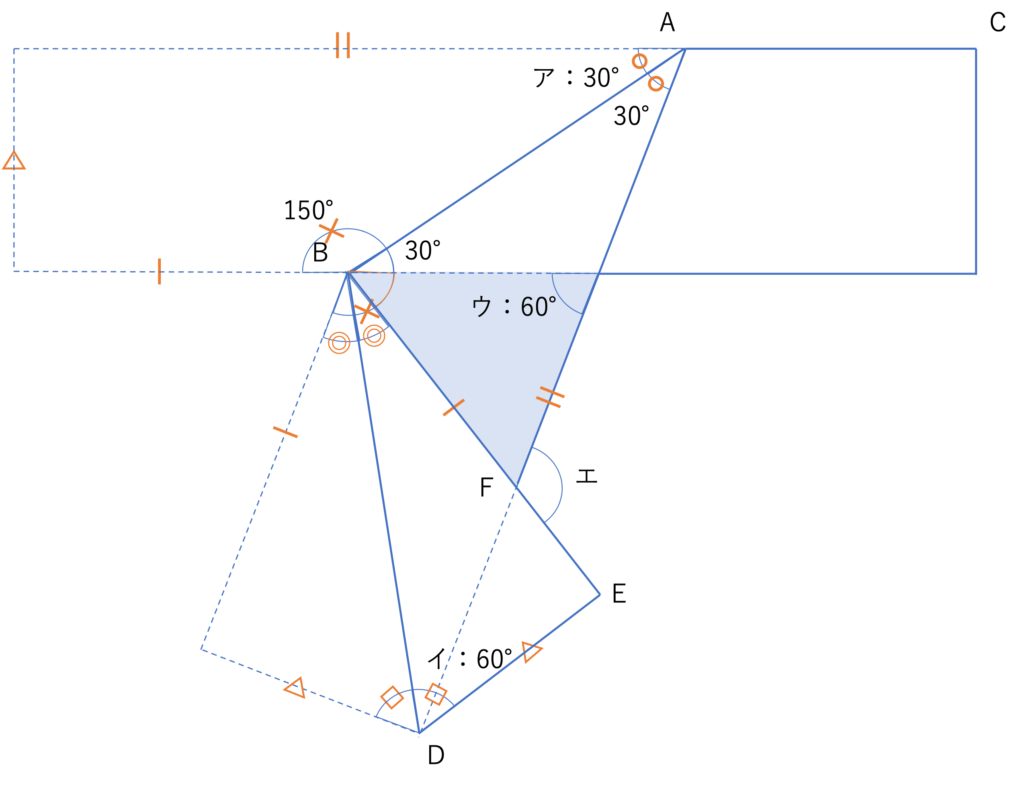
このオレンジで示した角度は×を折り返した角度から◎の角度2つと30°を除いたものとみなせますね。いま×の大きさは150°だと求まっているので◎の大きさを考えていくと,この部分は三角形BDEの内角の1つであり,角BDEが60°・角BEDが90°であることから180°-(60°+90°)=30°だと分かります。それゆえこの部分の大きさは150°-(30°×2+30°)=60°となりますね。よってオレンジでマークした角度とウの角度を足したエの値は60°+60°=120°となります。今回は対応関係だけでなく内角・外角の性質なども使用したので,もし忘れてしまった方は振り返っておくといいでしょう。
A.角ウ:60°,角エ:120°
終わりに
本記事ではこれまで,難関校で出題されるような難しい問題を引用しながら,発展的な解き方や問題の読み取り方等についてご紹介していきました。ここで登場した問題がそのまま受験に出てくるわけではありませんが,似たような複雑な問題はたくさん出てくるはずです。そこで下記のおすすめ記事や参考書籍を使いながら,平面図形に関してさらなる知識を蓄えていきましょう。今後の学習のお役に立てば幸いです。

















