今回は立体の展開図に関する問題の攻略法をご紹介いたします。空間図形の分野では幅広い問題が出題されていますが,展開図を使う問題はその中でも頻繁に登場します。対策は欠かせません。
本記事では展開図の問題を解けるようになるために,まず基本となる考え方を整理していきます。その後例題をいくつか引用し,この考え方を身につけるための演習を積んでいきます。問題だけ解きたい方は,「問題を解いてみよう」から進めてください。
Contents
それぞれの立体の展開図
それでは初めに例題を扱う前に,まずは問題を解くコツをご紹介します。そのコツとは立体の展開図を覚えておくことです。展開図の問題は,まず立体を展開する作業が必要となりますが,その上で線分の長さなどを計算しなければなりません。つまり展開図を考えるのは問題を解く上での第一歩でしかないのです。
そこで様々な立体の展開図を暗記しておくと,考える時間を短縮することができます。それは計算の部分で使う時間,また他の問題を解く時間を増やすことに繋がります。したがって考えのベースとなる展開図を覚えておくことは重要です。
そして覚えるだけではなく,頂点などの位置関係を掴んでおくことも大切です。立体は展開するだけが全てではありません。展開した図に点や線の情報を書き入れる必要もあります。そして正確に書き入れた情報から面積や線分の長さを求める問題もあるため,さまざまな情報とセットで展開図を覚えなければなりません。
以下ではいくつかの代表的な立体の展開図をご紹介します。このとき頂点と頂点の位置関係に気をつけておきましょう。ダッシュ(「’」「”」のこと)で示された点は,組み立てたときにダッシュ無しの点と重なることを指します。下の問題を解くときにこの展開図を参考にしてみてもいいでしょう。
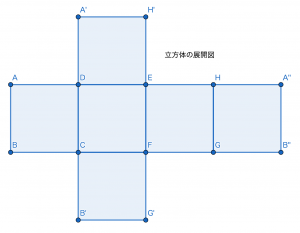
立方体・直方体
まずは立方体と直方体,つまりは六面体の展開図をみていきます。六面体は主にサイコロの関連する問題で出題されることが多いです。このような図形になるので覚えておきましょう。

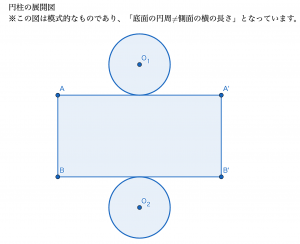
円柱・角柱
次に見ていくのは円柱と角柱です。この2つの図形は他の立体に比べて出題されることは少ないです。余裕があれば覚えておく,くらいで良いでしょう。次のように展開することができます。角柱はここでは三角柱を見ることにします。四角柱・五角柱などは底面の形と側面の長方形の数を変えることで展開図を作ることができるので,試してみてください。
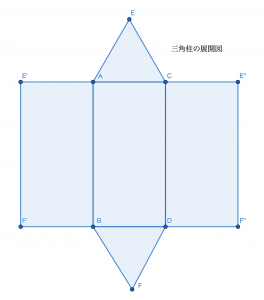
円錐・角錐
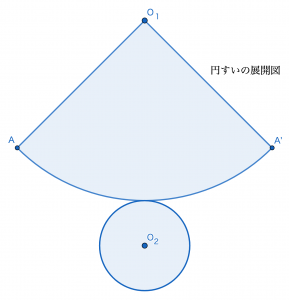
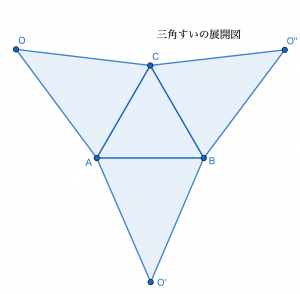
最後にみていくのは円すいと角すいです。このような図形は周囲にひもを張る,というような問題で展開図が絡んできます。下の図のようになるので暗記しておきましょう。ここでは角すいは三角すいを扱うことにします。四角すいなどは,上の角柱同様に,底面の形・側面の三角形の枚数を変えることで,展開図を作ることができます。
ここまでのまとめ
以上が主要な立体の展開図になります。ただし展開は必ずしもこの図の通りになるとは限りません。例えば問題①で使われる展開図は上で紹介したものとは全く違います。しかし上のような基本の展開図を覚えていれば,その図を切り張りして対応することが可能です。
またこれらに当てはまらない複雑な空間図形もありますが,そのような問題は上の図形の組み合わせで構成されているため,基本の図形を覚えておけば難なく解くことができます。何より空間図形の応用的な問題は難関校のごく一部でしか出題されませんし,それも解けないことが前提として作られたというものがほとんどです。したがって上の基本を押さえておくことが最重要となるでしょう。
問題を解いてみよう
ではここからは展開図に関する問題を2つ取り上げて,知識を定着させていきましょう。よろしければまずは自分の力で挑戦し,その後下に続く解説を参照してみて下さい。
問題① 切断面と展開図
水平な台の上にある,1辺18cmのふたのある立方体の容器ABCD-EFGHに水を入れ,ふたを閉めました。この立方体を下の図のように辺BCが台に接するように45°傾けたところ,AP=FQ=DS=GR=6cmとなりました。このとき,立方体の各面に水が触れている部分を立法体に展開図に表しなさい。
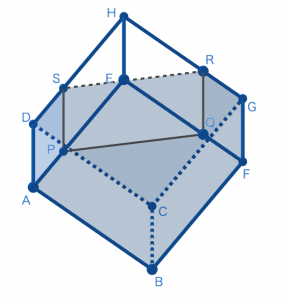
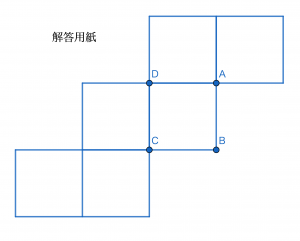
(逗子開成中学校(2015)、一部改題)
解説①
ここからは上の問題の解説をしていきます。問題文が長いため複雑そうに見えますが,これは要約すると,提示された立方体にある水面を展開図上に表せ,という指示が出ているだけの問題です。水面は平面PQRSを指すため,PQRSを構成する線分であるPQ・QR・RS・STを図に書き起こす必要があります。その作業が終わればあとは水と触れている部分を表すだけでよいので,まずは立体を展開してみましょう。
ここで,展開した形が指定されていましたね。この形に沿って立方体を切り分けなければなりません。上で示した基本の形とは少し異なりますが,点や線分の位置関係に注目すれば簡単に展開することができます。順番に考えていきましょう。
まず,与えられている辺ADと辺CDで作られる面を考えます。辺ADを持つ面は面ABCDと面ADEHの2つです。したがってAの左にE・Dの左にHを書き込めます。次に辺CDを同様に考えると,この辺を持つ面は面ABCD・面CDGHの2つなので,Cの上にG・Dの上にHを書き込めます。このような手順を重ねると,全ての点がわかります。
そうして書き込んだ展開図に,面PQRSを構成する部分をさらに書き込む必要があります。点Pから順番に図に表していきましょう。点Pは辺AE上にあり,AP=6cmを満たします。したがってこの指示通りの位置に点Aの隣に新たな点を打てばいいことがわかります。これと同様に点Q・R・Sも書き込み,問題で示されているように繋いでいくことで,面PQRSも展開図に表せました。このとき点Rと点Sだけは2箇所に書き込むことになり,不安に思うかもしれませんが,これは辺DH・辺GDに沿って展開されているために起こることなので,気にせず書き込んで下さい。
以上をまとめると,次のような平面図形ができます。A’やB’のようなダッシュがついた点は,ダッシュなしの点と重なることを指します。
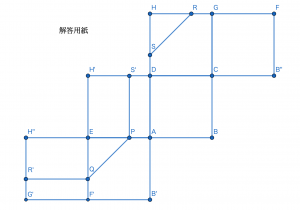
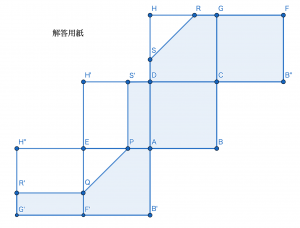
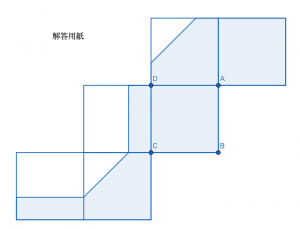
残りの作業はこの展開図のうち水と触れている部分を塗るだけです。水と触れている部分はあらかじめ問題の中で青く塗りつぶされています。よって立体を見て,当てはまる平面を塗りつぶしていけばよい,と見通しが立てられ,この通りに塗りつぶしていくと答えは次のようになります。このとき点を書き表す必要はありませんが,分かりやすいように点ありのものと点なしのものを載せておきます。
答え:下図の着色部
問題② 最短距離と円すい
母線の長さが6cm,底面の半径が1cmである円すいに,底面の周上の1点を通るように図のようなひもを巻き付けました。ひもの長さが最も短くなるとき,ひもの長さは何cmですか。
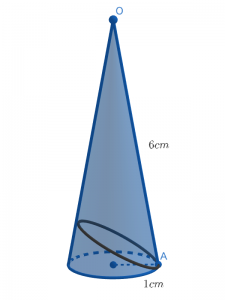
帝京大学中学校(2016)、一部改題)
解説②
それでは解説に移ります。ひもを側面に巻きつけているため,一度立体を平面上に展開することで簡単に考えることができそうだ,と見通しが立てられます。ここでは母線OAと底面の演習に沿って切り取ります。出来上がる図形は上で紹介したものと同じです。ここで基本の展開を覚えておくことが活きてきますね。
ここで巻き付けたひもが最も短くなるとき,そのひもはピンと張った状態であると想定されます。そしてひもは点Aから出発し,点Aに帰ってきます。したがって平面上でこのひもは直線で示すことができ,線分AA’と表すことができます。このひもも展開図に書き込みましょう。
以上のことから円すいは次の図のように展開されます。
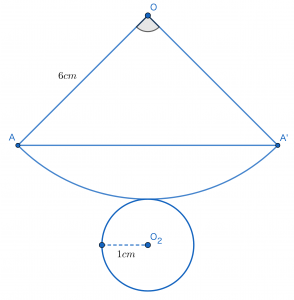
これらのことから,以下では線分AA’の長さを求めていきます。線分AA’は三角形OAA’の1辺であるため,三角形OAA’に注目しましょう。この三角形はOA=OA’=6cmである二等辺三角形です。
そして次に頂角の大きさを考えます。ここでおうぎ形AOA’に注目しますが,おうぎ形に関しておうぎ形の弧の長さ=直径×3.14×中心角÷360という公式がありました。三角形の頂角とはここでの中心角に相当するので,中心角を求めればよいとわかります。
ここでおうぎ形の孤の長さは底面の円周に等しく,つまりは6.28cmでした。直径は12cmであるため,6.28=12×3.14×中心角÷360と式を立てられます。これを整理すると中心角は60°だと分かります。したがって三角形の頂角は60°です。
これより三角形OAA’は頂角が60°の二等辺三角形,つまりは正三角形だと分かりました。よってOA=OA’=AA’=6cmとなります。したがって最小になるひもの長さは6cmです。
答え:6cm
最後に
今回は空間図形の展開図の問題について取り扱っていきました。ここで紹介した基本の展開図および例題はさまざまな問題の一部にすぎませんが,よく出題されるテンプレートのようなものなので慣れておくとよいでしょう。
また受験される学校によっては展開図が出題されにくいこともありますが,三次元の空間図形と二次元の平面図形を行き来する練習という意味では,他の空間図形の問題を解く能力も育むことができ,効果的であるのではないかと思われます。
本記事が今後の勉強の参考になれば幸いです。
(ライター:大舘)