本記事は中学受験に登場する資料の調べ方に関する問題を解く上で必要となる知識をまとめたものになります。資料の読み解き問題は算数ではたまに登場するものでしかないイメージがあり,おそらくつるかめ算をはじめとした特殊算や,平面図形・空間図形といった分野と比較してそこまで重点的に対策されるものではないと思われます。実際資料の読み解きはそこまで難しいものではありません。
しかし,だからこそこの分野からの出題があり,問題が解けなかった場合,多くの受験生と差がつけられてしまう可能性があります。またこの分野は算数に限らず,社会や理科などの他の科目でも出題されがちです。そのため今回は資料を読み解く上で重要な知識をまとめてみました。よろしければ復習の参考にしてみてください。
Contents
代表値
まずは代表値の復習から始めていきましょう。代表値とはデータを代表する数値のことになります。特に重要なのは平均値・中央値・最頻値です・最大値と最小値も代表値の一部ですが,これらは単純に最大のもの/最小のものを指しているだけなので,今回は省略します。
平均値
平均値とは,個々のデータを全て足し合わせた数を,数値の個数で割った値のことです。平均というものの計算自体はご存知かと思いますが,資料における平均の値が平均値の指す意味になるというわけです。
中央値
中央値とは,データを大きさ順に並べたときの真ん中に位置する数値のことです。したがって中央値を求める問題が登場したら,まず大きさ順にデータを並べ替える必要があります。数値の個数が奇数だったら真ん中の値は1つになりますが,個数が偶数だったときは2つの値が出てきてしまいます。このような場合は2つを中央値とするのではなく,2つの数値を足して2で割った値を中央値とします。
最頻値
最頻値とは,その名の通り最も頻繁に登場した数値のことです。簡単に説明すると,一番登場する回数の多い数値のことを指します。回数という観点から,最頻値が2つ登場する場合も想定されるのですが,そのときは中央値と違って2つとも最頻値とします。
例題を解いてみよう
ではこれらの代表値を覚えるために,簡単な例題を解いていきましょう。上の定義を参考にしても構わないので,よろしければ解いてみてください。
次の資料は,あるクラスの生徒10人の算数のテストの得点です。
10, 90, 70, 10, 70, 30, 20, 10, 30, 10
平均値,中央値,最頻値,最小値,最大値を求めなさい。
ではここからは順番に問題の答え合わせをしていきましょう。まず平均値ですが,これら10この数値を足し合わせると,(10+90+70+10+70+30+20+10+30+10)=350となります。このとき数値の個数は10個であるため,平均値の値は350÷10=35になります。
次に中央値を求めていきたいのですが,上の資料だと得点の大小関係がわからず,真ん中にある数字がわかりづらいです。したがって大きい順に並び替えた資料を新しく作ってみましょう。次のようになります。
10, 10, 10, 10, 20, 30, 30, 70, 70, 90
これで大小関係がわかりやすくなりました。数値の個数が10個であるため,今回は5番目の数字と6番目の数字の真ん中が中央値の値になりますね。したがって答えとなる中央値は(20+30)÷2=25です。
では最頻値はどうなるでしょうか。最頻値を求めるには,どの数値が何個あるのかをまず数えなければいけません。そのためここでの上で新しく作った大きい順の資料が役に立ちます。この資料を見ると,10が4個あることがわかります。
最小値・最大値も大小関係から考えるとわかりやすいですね。右端の値が一番大きく,左端の値が一番小さいため,最小値は10であり最大値が90となります。
A. 35,25,10,10,90
グラフ
次に資料の問題で登場するグラフについてまとめていきます。習ったグラフのうち資料問題で問われるものは主に次の4種類です。なお柱状グラフについては度数分布表のところで合わせて記載しています。
棒グラフ
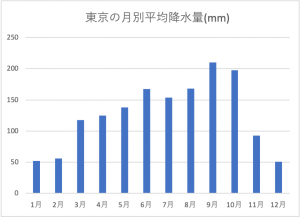
棒グラフとは数量の大小が比較しやすい資料になります。このとき比べられる数値は独立していて,どの数値がどの数値の何倍なのか,といった情報がわかりやすいです。下のような降水量のグラフが具体的な棒グラフの例になります。月ごとの降水量は互いに関連してはいません。4月の降水量が多いから5月の降水量は少ない,などという因果関係は見出せませんよね。したがって棒グラフに向いているデータとなります。
折れ線グラフ
折れ線グラフとは時間の経過などに応じて変わる数量の動き方を示すものです。横軸には時間が,縦軸には上の棒グラフとは違って連続量がきます。観測した点と点を線で結ぶため折れ線グラフという名前がついています。棒グラフは数量の差を比較するのに使われるのに対し,折れ線グラフは個々の数値の関連だったり,全体を通した変化の特徴だったりを調べるのに向いています。次のような気温の変化についてのグラフが折れ線グラフの具体例になります。

円グラフ
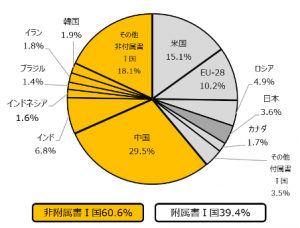
上の2つのグラフは降水量が何mmか,気温が何℃だったか,など個別の数量を表すものでした。それに対しこの円グラフは,全体に占める特定の数値の割合を示すものになっています。円グラフは更に,割合の大小がおうぎ形の面積の大小と一致しているため,割合を視覚的に捉えることができるという特徴も持っています。例えば,以下の各国別の二酸化炭素排出量の構成比についての資料が代表的な円グラフになります。
帯グラフ
帯グラフも全体に占める構成比を示す資料です。円グラフと異なるのは,帯グラフは他の帯グラフと並べて比較されることが多いということです。その場合比較対象は時間軸の違うデータや違う場所のデータなどになります。次の職業別就業者構成比についてのグラフが具体的な例になります。ここでは賛成と女性が比較されていて,女性と男性の間に見られる違いなどが一目瞭然になっています。

度数分布表・柱状グラフ
最後に度数分布表について振り返っておきましょう。この度数分布表・柱状グラフが中学入試の算数で最も問われやすい範囲です。柱状グラフはヒストグラムと呼ばれることもあります。
度数分布表はデータの散らばり具合を見るのに使われます。ある区間に含まれる数値の個数を数え,それをまとめたものがこの表です。そして個数をグラフ上に棒グラフのように表したのが柱状グラフです。
ただし棒グラフと違うのは,棒グラフはここの独立した数値を横軸に取るのに対し,ヒストグラムは区間を横軸に取るという点です。したがってヒストグラムの棒と棒同士はくっついています。試しに上の例題のデータを使って,度数分布表と柱状グラフを作ってみましょう。
10, 90, 70, 10, 70, 30, 20, 10, 30, 10
ここでの区間は20点ごと,つまり0点〜19点,20点〜39点,……,80点〜99点,100点と区間を設けることにします。100点だけ範囲になっていないのは,0点から100点までの数値の個数は101個だからです。ただし受験では自分で区間を設定することはないので,操作の意味がわからなくても安心して読み進めてみてください。
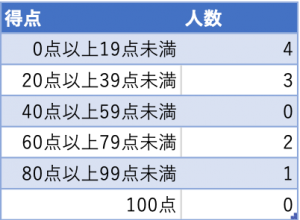
そしてこの人数と得点の関係をグラフ上に表すことで柱状グラフが完成します。
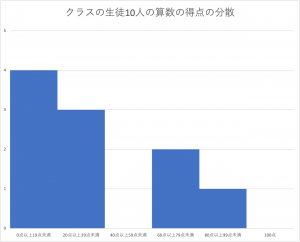
この問題では点数が低いグループと点数の高いグループに二分されることが分かります。このようにデータの散らばり具合が理解できるのが柱状グラフ・ヒストグラムです。横軸や棒の書き方に注意して覚えておきましょう。
最後に
今回は資料の調べ方問題を攻略するための知識の復習をしていきました。それぞれの特徴や形とセットで頭に入れておくといいでしょう。本記事が学力向上の手助けとなれば幸いです。
(ライター:大舘)

















