今回の記事では多角形の性質に注目していきます。よく目にする・耳にする多角形といえば三角形や四角形ですが,中学受験ではこの他に様々な図形が登場します。そのため有名な図形の性質だけにとどまらず,いろいろな場面や問題に対応できるような知識を身につけておかなければいけません。この記事ではその一部として内角・外角・対角線に着目した内容をお教えしていきますので,よろしければ参考にしてみてください。
多角形とは…?
それではまず多角形の性質を見ていく前に,そもそも多角形とはどのようなものかということに注目して前提となる知識を確認していきましょう。多角形と言われると三角形,四角形,五角形という単語を想像するとは思いますが,一般的に多角形とは3つ以上の線分,つまりは辺に囲まれた図形のことを指します。3つ以上とされている理由は,線分が2つ以下だと図形を作り出すことができないからですね。そしてこの図形を構成する辺の数,または線分同士をつなぐ頂点の数で,その図形が○角形だと決まるわけです。例えば辺の数と頂点の数が3つであればその図形は三角形であり,4つであれば四角形であり,となります。当然のことかもしれませんが,まずは○角形の辺と頂点の数は○個であるということを覚え直しておきましょう。
内角の性質
さて多角形とはどういうものかを確認したところで,続いては本題の内角の性質から解説していきます。まず内角とは多角形の内側に存在する角度のことを指します。例えば以下のような三角形や四角形があったとして,それぞれの頂点において隣り合っている2つの辺が作っている多角形の内側に向いた角のことが内角となるわけです。この図から,それぞれの頂点について内角が1つ対応して存在することが分かります。
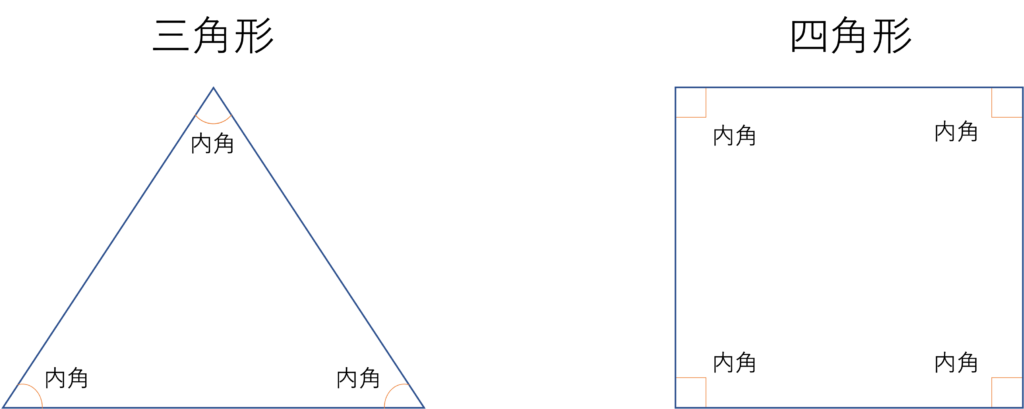
今回見ていくのはこの内角同士の関係性です。前述したように三角形には3つの内角が,四角形には4つの内角が存在しているわけですが,それらはどういう関係で結びつけることができるのでしょうか。ここで重要になってくるのが内角の和という言葉です。多角形上に存在する内角を全部足し合わせたときの大きさを内角の和というのですが,この内角の和はその図形が何角形であるかによって定められます。よく耳にするのは三角形の内角の和は180°であるということでしょうが,これを一般化したときに○角形の内角の和は180×(○-2)°であるとまとめることができます。
その理由は○角形の中には○-2個の三角形が存在するからです。例えば四角形であればその形は対角線で三角形2個に分けられますが,このときそれぞれの内角の和は180°なので四角形の内角は180°×2=360°と導くことができます。これと同じように考えると五角形は3個の三角形に,六角形は4個の三角形に,……○角形は○-2個の三角形に分けられるので,それぞれの内角の和は五角形であれば180°×3=540°に,六角形であれば180°×4=720°に,……,そして○角形であれば180×(○-2)°に,とまとめられるわけです。
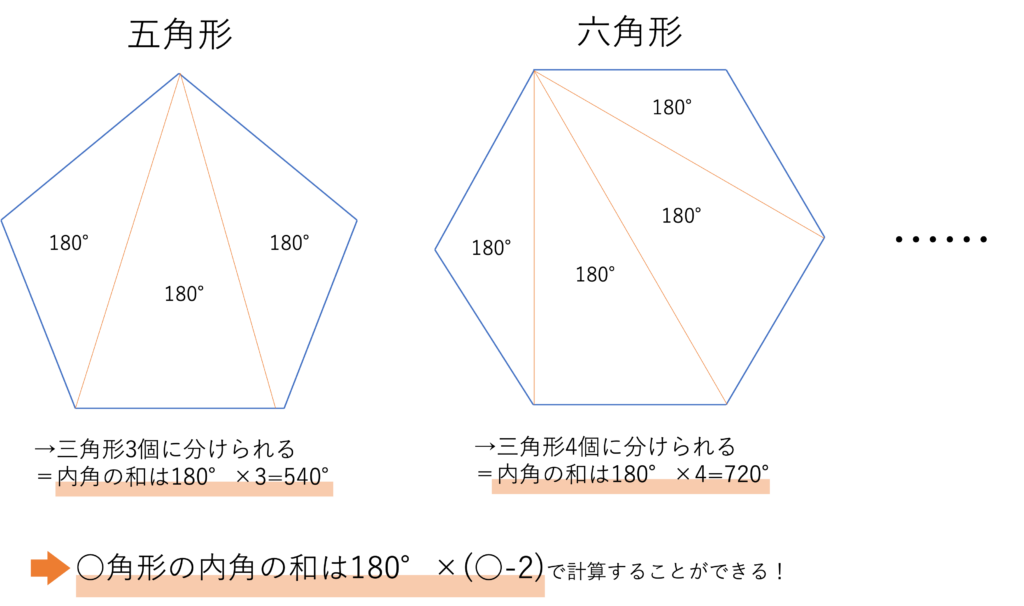
この内角の和という性質はどの平面図形の問題を解いていく上でも重要になってくるポイントですので,ぜひ忘れずに頭の中に入れておきましょう。
外角の性質
続いて外角の性質について説明していきます。外角とは多角形の1辺を延長させた線分と,その辺と隣り合っている辺とが作り出す角度のことです。内角は図形の内側を向いていましたがこの外角は図形の外側を向いていて,多角形において対になっている要素だとみなすことができます。ここでよくありがちな間違いとして,内角の反対だからという覚え方をしているばかりに内角を取り囲むように存在する大きな角のことを外角だと思ってしまうというミスが存在します。しかし外角とは延長した辺における角度なので,例えば三角形と四角形なら次のような部分を外角と呼ぶことができます。正確に覚えておきましょう。
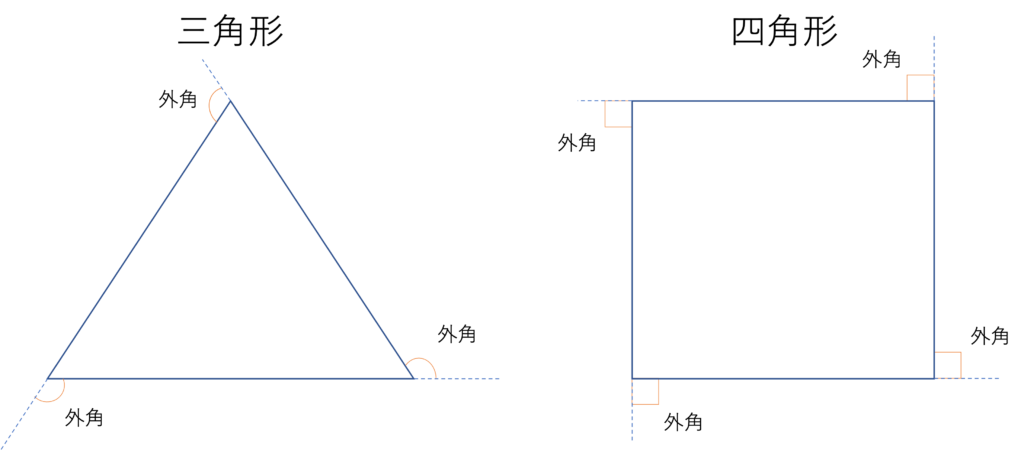
さて上の図でご覧いただいた通りこの外角も,内角と同じように多角形において頂点の数だけ存在するのですが,ここでは外角の和について考えていきましょう。内角の場合は多角形の頂点が増えるほど内角は大きくなっていき,その関係は180°×(○-2)とまとめられましたが,外角の和はどの図形・どの多角形においても360°になるという性質があります。その理由は外角を180°から内角を引いた角度として捉えたときの計算の結果から導くことができます。例として五角形の外角の和を考えてみましょう。いま上の図で見たように外角は180°-内角と表すことができますが,五角形には5つの外郭が存在するのでそれらに番号を振ると,外角の和は外角1+外角2+外角3+外角4+外角5と書くことができますね。それらを内角との関係で書き換えると,下のような式が出来上がります。
外角の和=外角1+外角2+外角3+外角4+外角5
=(180°-内角1)+ (180°-内角2)+ (180°-内角3)+ (180°-内角4)+ (180°-内角5)
=180°×5-(内角1+内角2+内角3+内角4+内角5)
ここで五角形の内角の和は先ほど見た関係から180°×(5-2)=540°だと計算できるので,上の式は900°-540°=360°となるわけです。以上の計算は五角形に関する計算でしたが,この計算は六角形,七角形,……と頂点と辺の数を増やしていっても当てはまります。どの図形においても外角の和は180°を頂点・辺の数だけ倍したものから内角の和を引くことで,もっと一般化すれば○角形の外角の和は180°×○から内角の和である180°×(◯-2)を引くことで計算できるということから,多角形の外角の和はどの図形でも360°だと言うことができます。どの部分が外角かという要素と合わせて忘れやすいところなので,正確に頭に入れておきましょう。
対角線の性質
最後に見ていくのは多角形における対角線の性質です。ご存知の方が多いかもしれませんが,対角線とは多角形の隣り合わない2つの頂点を結んだ線分のことを指します。隣り合わないという条件がついているのは,隣り合った頂点を結んでしまうとただの辺にしかならないからです。この章では多角形の対角線の本数が何本かを考えていきましょう。まずは一例として三角形と四角形の対角線の数を考えていくことにします。
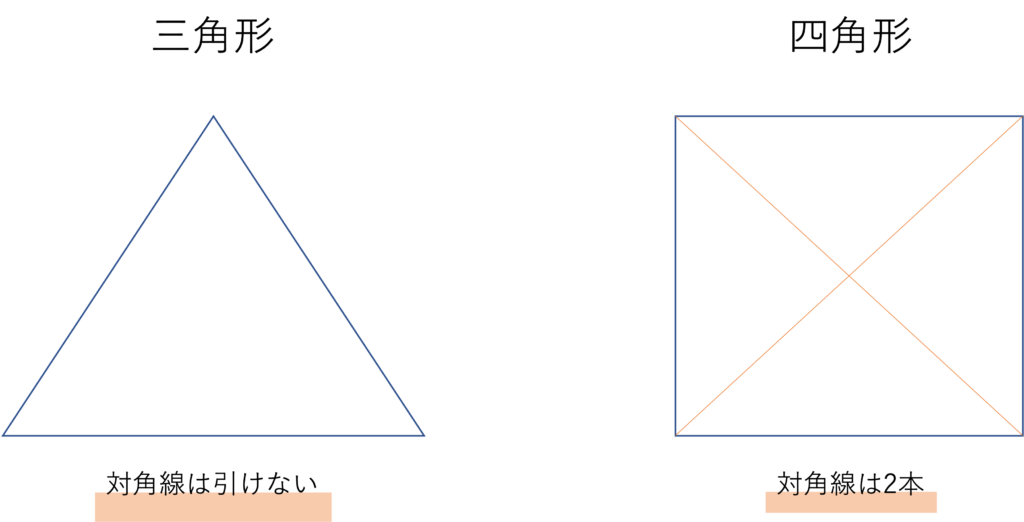
この図から,どの頂点同士も隣り合っている三角形には対角線が存在せず,四角形には2本の対角線が存在することがわかりました。これと同じことが五角形や六角形でもいえるかどうか,そしてそれらの関係をどのようにまとめればいいのかを導いていきましょう。まず前提として,対角線はある2つの頂点を結ぶものです。それゆえ対角線の出発点となる片側の頂点を固定して何本の線分が弾けるかを考えていきます。例えば下のような五角形や六角形の場合,1つの頂点からはそれぞれ2本・3本の対角線が引けると分かります。これは隣り合っていない頂点の数と等しいですね。五角形のある頂点には,その頂点自体と隣り合った2つの頂点には線が引けないので5-3=2で残った2つの頂点に対角線が引けるわけですし,六角形のある頂点においても同じことが言えるので6-3=3で残った3つの頂点に対角線が引けるわけです。
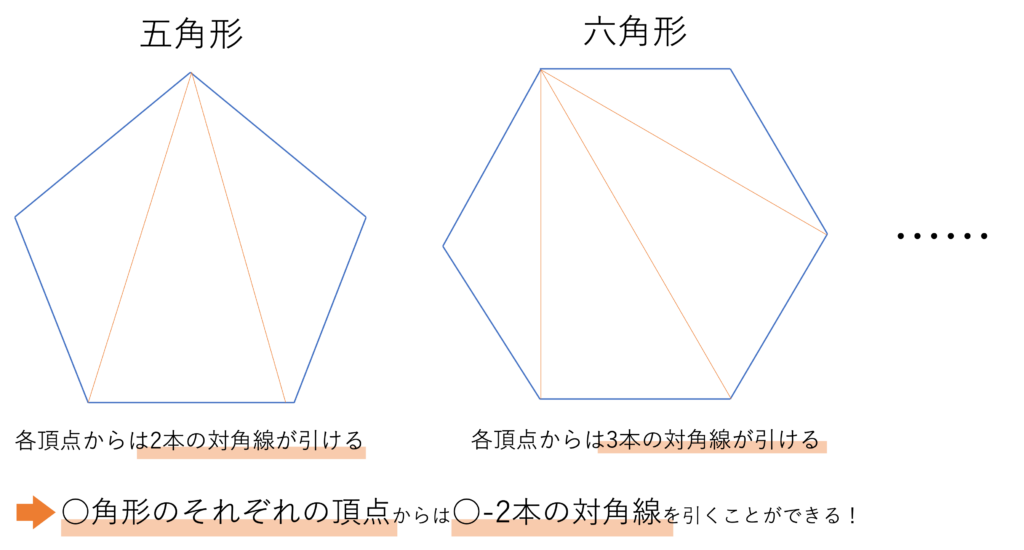
さて各頂点に対して五角形なら2本,六角形なら3本の対角線がつなげられるわけですが,この対角線は全ての頂点から引けますよね。そのため五角形なら頂点が5つあるので2×5=10本,六角形なら頂点が6つあるので3×6=18本の対角線を引くことができます。以上のことから五角形と六角形,さらには多角形全体の対角線の数が分かる……と言いたいところなのですが,ここで気を付けておくべきポイントがあります。それはここまでの計算だと1本の対角線を2回カウントしてしまっているという点です。例えば五角形の頂点Aと頂点Bを繋いでいる対角線があったとして,上の考え方だと頂点Aを出発点とした場合と頂点Bを出発点とした場合の2回で計算が進められてしまっているわけです。そのため余分に数えてしまった2回分を半分にして数えなければならないので,上で求めた対角線の数を2で割ることで,正しい対角線の数を求めることができますね。したがって五角形の対角線の数は10÷5=2本,六角形の対角線の数は18÷2=9本となるわけです。
これらの計算過程から,すべての多角形における対角線の関係を一般化して○角形における対角線の数を考えたとき,○角形のそれぞれの頂点からは○-2本の対角線を引くことができ,その対角線が○個の頂点の分,つまり(○-2)×○本引くことができますが,そのうち半分は被っているものを2回カウントしているので対角線の数は(○-2)×○÷2本であるとまとめることができます。考え方はやや難しいですが式そのものは簡単ですので,まずはこの式の形を覚えた上で考え方を頭に入れていくといいでしょう。
まとめ
- ○角形の辺と頂点の数は○個!
- ○角形の内角の和は180°×(○-2)°になる!
- 多角形の外角の和は辺・頂点の数が変わっても360°で変わらない!
- ○角形の対角線の数は(○-2)×○÷2本になる!
終わりに
今回の記事では多角形の性質について,特に内角・外角・対角線の3要素を中心に解説していきました。これらの性質をはじめ,図形に関する基礎的な知識は早めに身につけておきたいところです。本番を意識し始める頃には応用問題をメインに解かなければいけないため,出来るうちから頭の中に基本的な事柄を入れていくという意識で勉強していきましょう。本記事が今後の学習のお役に立てば幸いです。


















