今回の記事では調べ・推理・計算の条件に関する分野を解説してくシリーズの第1本目として,数の大小にテーマを当てた問題の解き方を解説していきます。この問題で重要になってくるのは数学的なセンスというよりは国語力・読解力であり,普段とは違った頭の使い方をしなければならない分,対策が不可欠です。よろしければ本記事をご参考に,対策を進めていただけますと幸いです。
Contents
「調べ・推理・条件の整理」とは?
まずは今回の解説の前提となる,調べ・推理・条件の整理とはどのような問題を指すのかを確認していきましょう。この分野の問題は簡潔に言うと,与えられた問題文の条件をもとに推理を重ねていき,答えを導いていくというものです。これだけだと普通の文章題と変わらないように感じるかもしれませんが,この分野と他の算数の文章題の一番の違いはなぞなぞみたいな構成をしており,数字や計算式が使われない点にあります。つまり算数のセンスが問われない分,頭の回転に頼らざるを得ない構造をしており,そのため小学校低学年のお子様でも解く事ができたり,反対に小学校高学年のお子様でも解くのに苦戦したりしてしまうのが調べ・推理・条件の整理という範囲だと言えますね。
この分野の問題は,与えられる条件や要件の特徴に応じていくつかのジャンルに分類する事ができます。その一つに方陣算なども挙げられるのですが,今回は中でも頻出の数の代償に関する問題を取り上げていきます。
「数の大小」問題とは?
さてこの数の大小問題ですが,この分野ではその名の通り,いくつかの数字の大小関係を考えていくというシチュエーションの問題が登場します。基本的にはいくつかの数字のアルファベットで表され,その和・差・積・商の関係が与えられるのですが,その値をもとに頭を動かしていくと言う意味で,普段の算数の文章題と違った難しさがあります。このジャンルでは例えば次の2つのような問題が登場することが多いです。数字を表すいくつかのアルファベットが存在し,それらのうち2つの数の関係が与えられていたら数の大小問題だ,と考えてしまっていいでしょう。
4つの整数A,B,C,Dについて,次のことがわかっています。
①Aは最も大きい,②AはBより6大きい,③BはCより4小さい,④CとDの差は8
このときA,B,C,Dを大きい順に答えなさい。
3つの整数A,B,Cについて次のことがわかっています。
ア:AとBの差は5,イ:BとCの差は4,ウAはCの2倍
このとき一番大きい数と一番小さい数はいくつになるでしょう。
ちなみにこの調べ・推理・条件の整理という分野の問題では,この他にも集合に関する問題や順位に関する問題,てんびんを使った問題といった様々な種類の形式の問題が出題されます。それらについても今後の記事でご紹介しますので,ぜひ一読していただきたいです。
解答のポイントは線分図!
それではこの大小関係を紐解いていくためにはどうやって問題と向き合っていけばいいのでしょうか。ここで挙げられる解き方の一つが線分図によるものです。他の文章題でこの線分図というテクニックは度々ご紹介していますが,一見算数の問題っぽくはないこの数の大小問題でも,線分図を使えば無事に解くことができます。
ただし線分図と一口に言ってもその使われ方は様々ですし,線をとりあえず引いてみたはいいもののどうやって図を書いていけばいいのか分からないと感じる人も多いと思われます。そのためここからはどうやって線分図を書いていけばいいのか,どうやって正しい解答を導いていけばいいかという解答ステップを,先ほどの例題を使いながらご紹介していきます。ここで,改めて数の大小問題の例題を貼り付けておきます。
4つの整数A,B,C,Dについて,次のことがわかっています。
①AはBより6大きい,②BはCより4小さい,③CとDの差は8,④Aは最も大きい
このときA,B,C,Dを大きい順に答えなさい。
まず大事になってくるのが,それぞれの条件で表されている事柄を一つずつ線分図に表していくことです。この問題だと4つの条件が登場していますので,まずは①から順番に線分図を書きながら,AからDまでの4つの数の関係をまとめていきましょう。
条件を一つずつまとめよう!
まずは①のAはBより6大きいという条件について考えていきましょう。といってもこの条件はそこまで難しく考える要素のない条件ではありますので,次のようにAを表す線分を1本書き,そのAと比べながらBを表すのに適切なぐらいの長さの線分を引いてあげれば問題ありません。簡単なところはとことんまで省略しながら,短い時間で正解に辿り着く努力を怠らないようにしましょう。
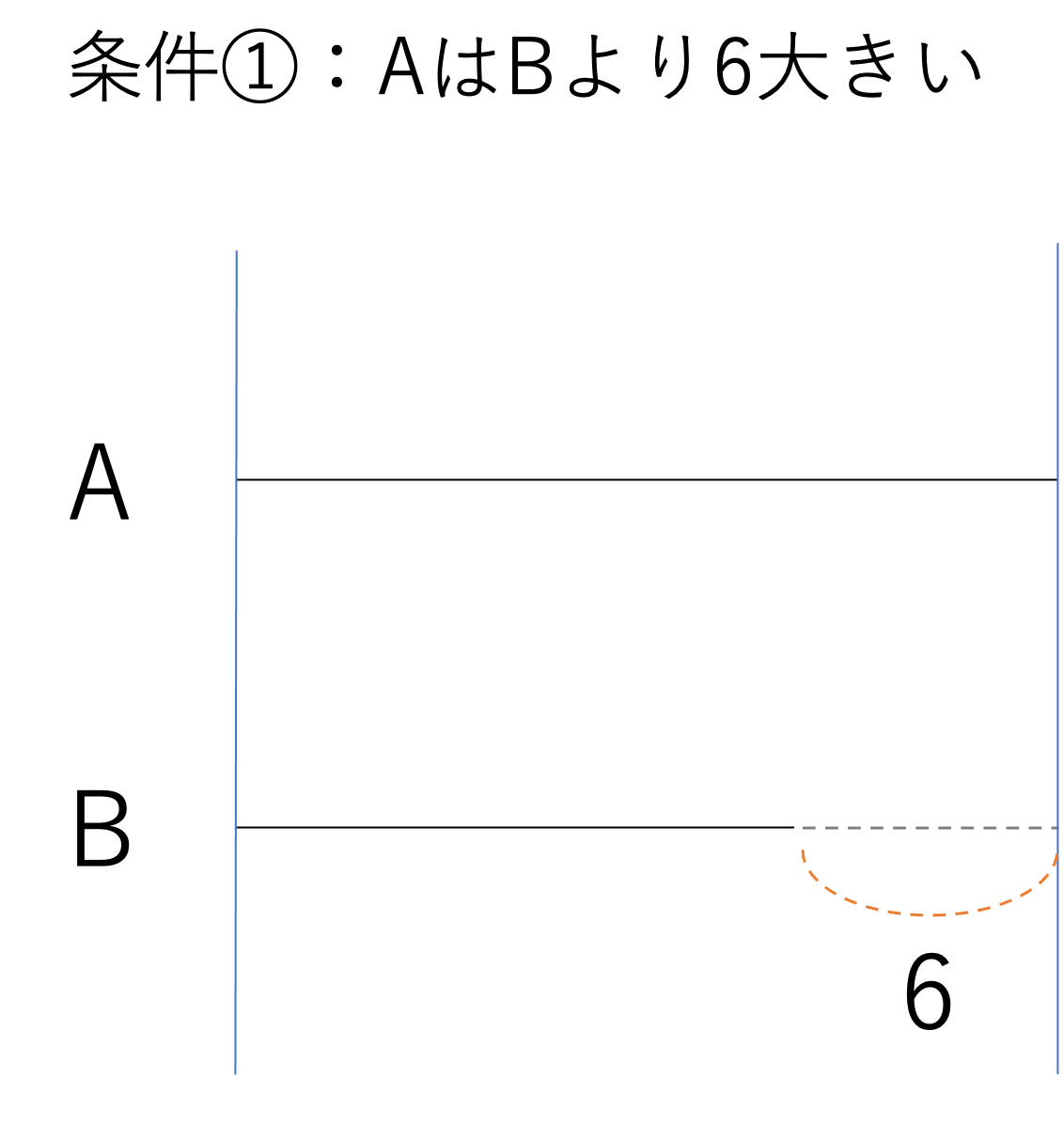
この調子で条件②についても考えていくと,次のような線分図を得ることができます。なおこれらの条件を考えていくとき,慣れてしまえば大丈夫かもしれませんが,何が何より大きいのか・小さいのかという言葉遣いにはきちんと注意しておく必要があります。「AがBより」と「AよりBが」では意味が反対になってしまうように,こういう読み取りにおけるケアレスミスが命取りになりやすいのがこの単元です。気をつけながら解き進めていきましょう。

いくつかのパターンが考えられる場合には…?
では続いて③の条件も線分図に,と進めていきたいところですがここで大きな問題が出てきてしまいます。この「CとDの差は8」という条件ですが,これだけだとCの方が大きいのかDの方が大きいのか判断することができません。このように調べ・推理・条件の整理の問題では,いくつかの場合が考えられるという状況が登場しやすいです。というよりも,そのような複数考えられるパターンを他の条件と照らし合わせることで削っていく,ということに出題者の意図があると考えてもらった方がいいでしょう。そのため今回の問題でも,一旦③の条件のみを考えるステップでは2パターンの線分図を書くことで,中身を整理することに集中していきましょう。
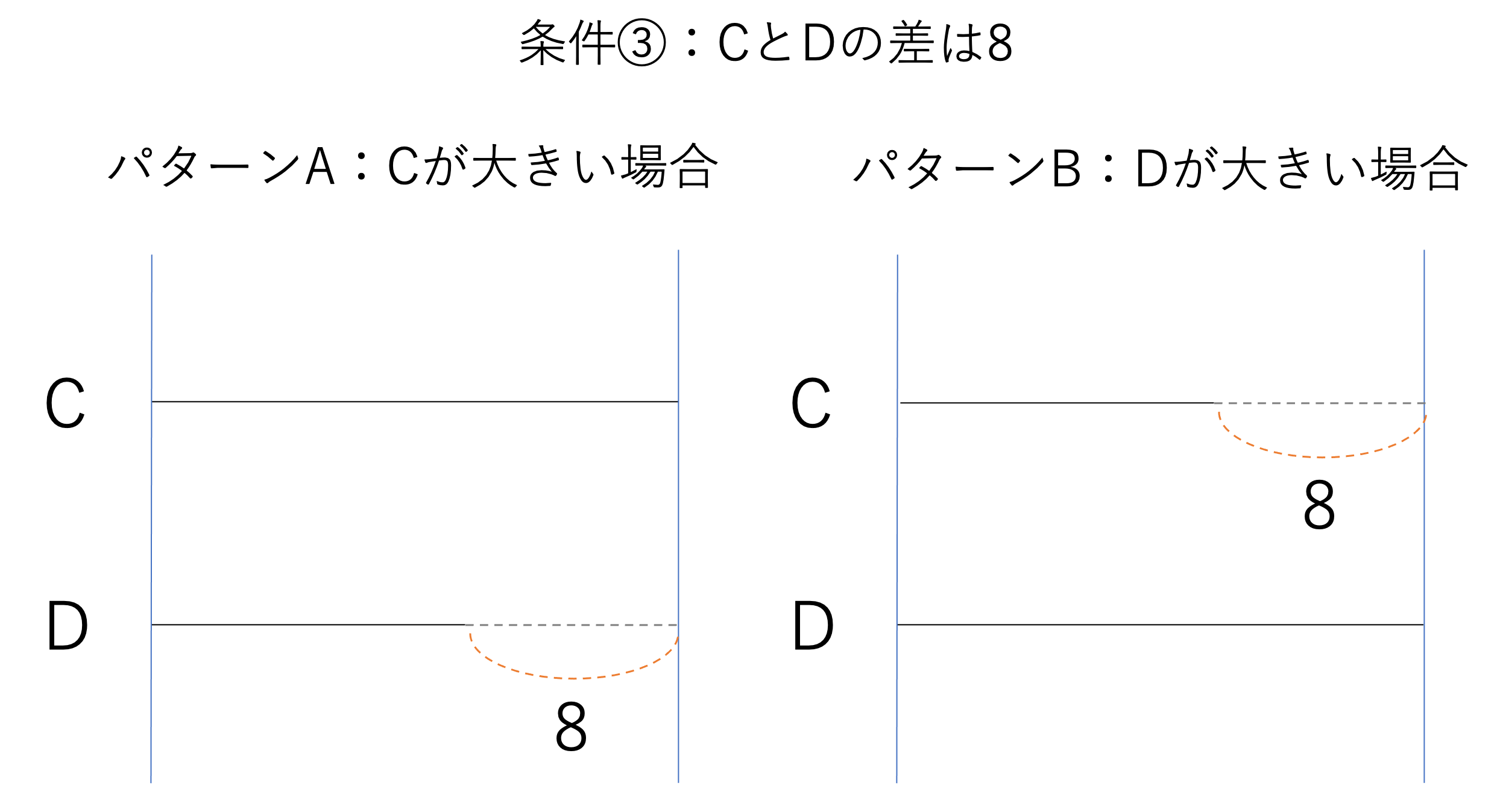
なお最後の条件④ですが,こちらはB・C・DよりもAが大きいという数字が絡まない条件なので線分図に書くことは省略します。もちろんあえて書くことができますが,省略するべきところは省略して手早く計算することが中学受験では重要ですので,最大・最小という言葉は最後に条件をまとめるときに忘れずに考えていくだけで十分,とみなして進めていきましょう。
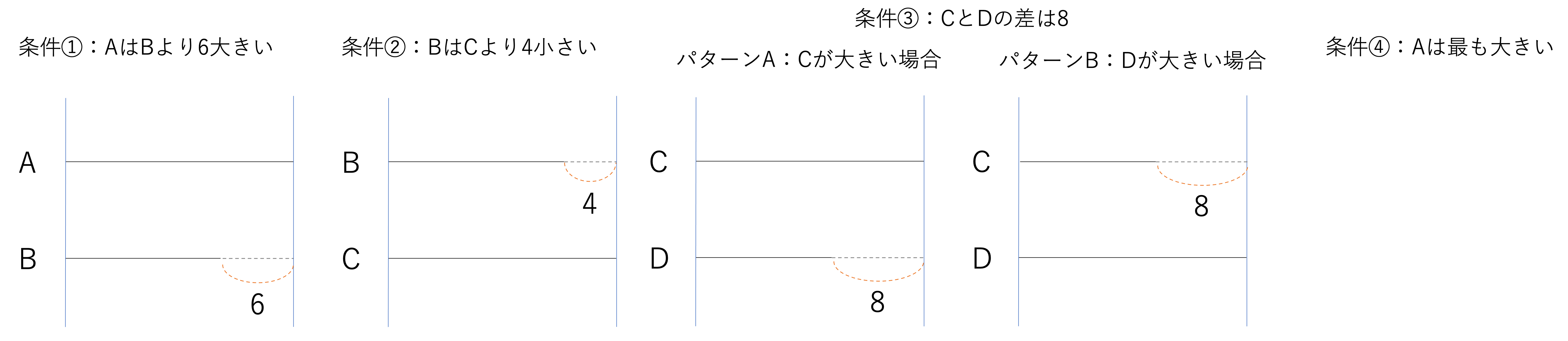
全ての条件をまとめよう!
それでは最後にすべての条件をまとめて今回の問題の答えを導いていきましょう。あらためて4つの条件をまとめると次の図のようになります。
ここで悩ましいのが条件③における2つのパターンの処理ですが,まずは焦らず初めの2つの条件を中心に線分図をまとめていきましょう。この手の問題で重要なことは,分からないところで悩み続けるのではなく分かるところから一つずつ解決していくことです。急がば回れではありませんが,情報をどんどん整理していく過程で解き方が思い浮かんだりすることは少なくありません。そのため手を動かし続けることを意識しておくといいでしょう。

このように条件をまとめることができたので,最後に条件③の2つのパターンを解決することで答えを導いていきましょう。2つの場合が存在するこの条件③ですがその解決方法は至ってシンプルで,それぞれの場合において大小関係がどのようになるかを考えていけばいいですね。いうまでもなく答えは1つに絞れますから,2つパターンがあればどちらかは必ず何らかの条件にそぐわないようになっています。そのため4つの条件を見つつ,全てに当てはまっているかを確認していきましょう。まずCが大きい場合ですが,こちらはDがBより4小さくなり,最大がA・最小がDになりますね。この関係はとりわけ問題がなさそうです。他方Dが大きい場合を見ていくと,この場合DはBより12・Aより6大きい数字となり,最大がD・最小がBになりますが,これは4つ目の条件である「Aが最大である」という条件に合致しませんね。それゆえ今回はパターンAが正解となるため,整数は大きい順にA,C,B,Dとなると言えるわけです。
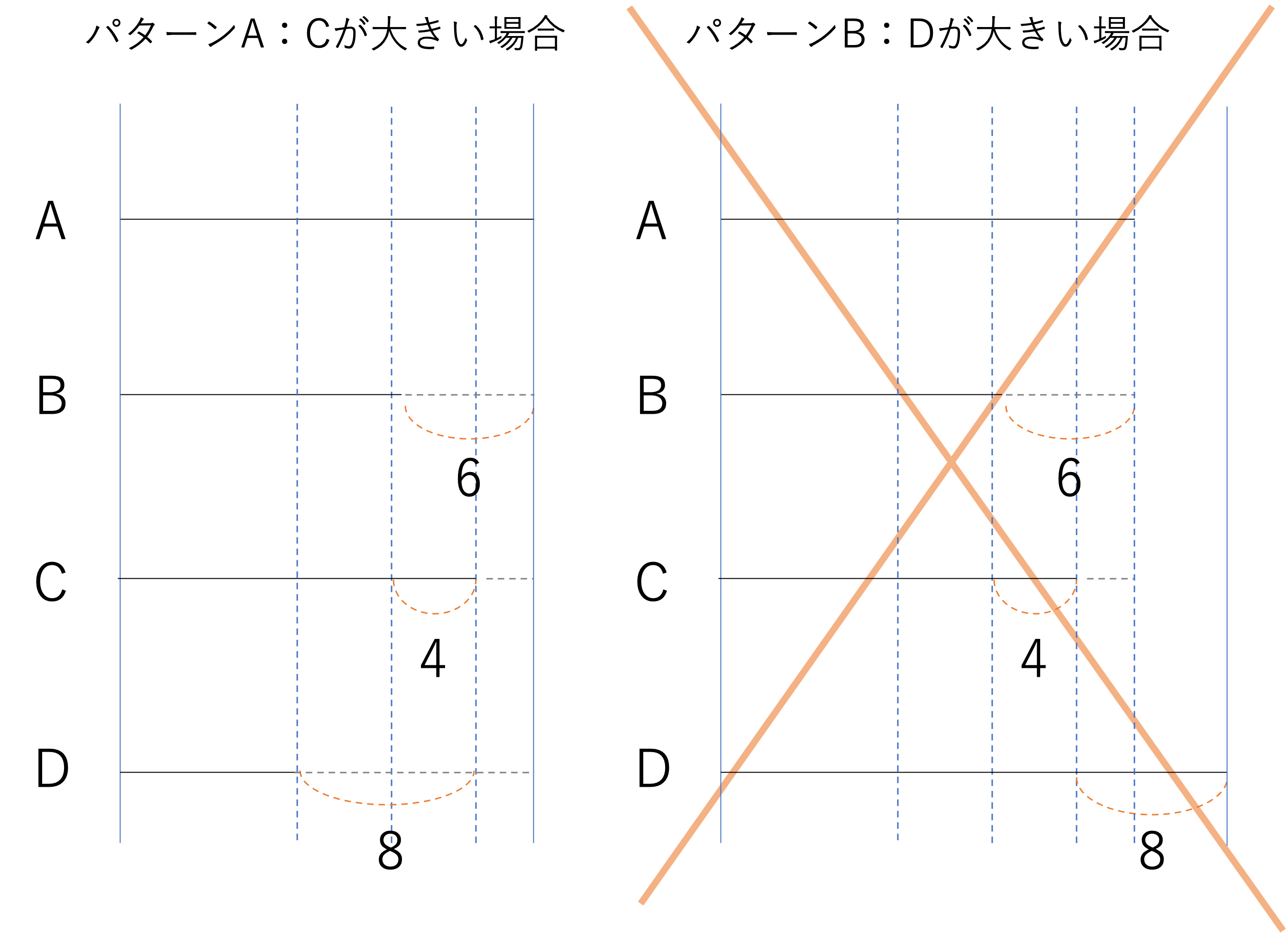
A.A→C→B→D
まとめ
数の大小問題を解く上で重要なのは以下の手順を踏むことです。もちろん頭の中で計算や考えを完結させることができるのが理想ですが,初めの慣れないうちや,受験本番で緊張してしまったときは,このステップに則って解いてみてください。
- まずは用語に注目して数の大小問題かどうか見分ける!
- 線分図を使いながら一つ一つの条件を整理する!
- このとき場合分けにも注意しよう!
- 条件をまとめて適合しないパターンは省こう!
終わりに
今回の記事では数の大小問題に着目して,その特徴や攻略法をご紹介してきました。前述したようにこれらの問題では頭の動かし方が普段の算数の問題とは異なるため苦戦する人も多いでしょうが,基本の線分図に則っていけば無事正解に辿り着けます。そのことを忘れずに問題に立ち向かっていただけますと幸いです。よろしければ下のおすすめ記事や参考書籍を活用しながら,さらなる学力向上に励んでいきましょう。


















