この記事では、中学数学の中でも、全く新しい考え方をする単元で、理解できないとどんどん置いてかれていってしまうような「一次関数」について「そもそも関数とはなにか?」「グラフとはなにか?」ということについてのイメージを掴むことを目指していきます。
目標は下の問題を解くことです。
問題
\(y=-2x+8\)という一次関数がある。この時、以下の問いに答えよ。
(1)\(x=4\)の時、\(y\)の値を求めよ。
(2)この一次関数のグラフを描け。
それでは、一歩一歩、進んでいきましょう!
Contents
「関数」とは「オルチャンメイク」のことである
「メイク」について考えてみましょう(男の子もね)
さて、一次関数について理解して、問題を解けるようにするために、一つ一つの言葉の意味を勉強しましょう。まず「関数」という語から。
ところで、読者の皆さんは、昔の女優さんを見たことがありますか? もし見たことがあるならば、みんな同じような雰囲気をしてるなという印象を持ったことでしょう(キリッとしてるな、とか)。
そして、今の女優さんを見てみると、こっちはこっちでまた同じような雰囲気を持っていると思います(「やわらかい」印象というか)。
これは、化粧の仕方に流行があるからです。「ゆるふわメイク」「オルチャンメイク」「チャイボーグ」……。でも、それぞれの顔は違うから、同じ化粧の仕方をしていても、各々の良いところを目立たせたり、気に入らないところは隠したりして、少しずつ、雰囲気は似ていても別の顔になっているでしょう。

さまざまなメイクには名前があります
だから、こういうことが言えます。
ある顔の人が、「オルチャンメイク」をすると、こういった顔になる。
他の顔の人が、「オルチャンメイク」をすると、雰囲気は似てるけど、さっきとは違った顔になる。
また別の顔の人が、「オルチャンメイク」をすると、似た雰囲気でも、また違った顔になる。
実際は、それぞれのメイク後の顔は微妙に違っています(そして、おまけで言っておくと、オルチャンメイクは「こんな感じ」の顔にはなりません)
数学で「メイク」してみる
それぞれ別のものがそれをすると違った結果を生み出す、ここでの「オルチャンメイク」のようなものが、ちょうど、関数です(やっと話が数学に戻ってきましたね)。
\(y=-2x+8\)は、この「メイクの仕方」の数学版だと思ってください。似た他の式(例えば\(y=5x-2\))は、また別の「メイクの仕方」。
ある顔の人の代わりに、数学で、この「メイク」をするのは、\(x=0, x=1, x=2\)とかの、\(x\)の値です。
これがメイクをすると、\(y=-2×0+8=8\)のようにして、「メイク後の顔」が、\(y=8\)という\(y\)の値として出てくる、\(x=1\)ならば、\(y=-2×1+8=6\)で、また違った「顔」(\(y\)の値)が出てきます。
このようにして、ある値を入れた時(数学ではこれを「代入」と呼びます、この言葉は覚えましょう!)に、それに一定の操作(メイク!)を加えることで、別のただ一つの値を出す、決まった操作(メイクの仕方!)を「関数」と呼びます。
「一次」関数というのは、その関数の特定のタイプで、\(y=-2x+8\)のように、\(x\)が、分数の分母でない仕方で書いてあって、かつ右肩に数字が書いていない場合のことを指します(厳密には「次数が1である」ということなのですが、この点は今は難しいので置いておきましょう)。
(1)を解く
これで(1)が解けると思います。
今は、\(x=4\)を代入して、「メイク」してやれば良いので、
\(y=-2×4+8=0\)となって、\(y\)の値が\(0\)ということになります。
節のまとめ
ある値を代入した時、その値を操作して、その値に応じた、別のただ一つの値を出すもののことを、数学では「関数」と呼ぶ。「一次関数」とは、そのうち、\(y=-2x+8\)のように、\(x\)が分数の分母にない仕方で書いてあり肩に数字の書いていないもの(=次数が1のもの)のことである。
「グラフ」とは「山」のことである
グラフ=みんなが「メイク」した結果!
次に、「グラフ」について。
「グラフ」とは、さっきの例えを続けるのならば、「あなたにこのメイクをするとこんな顔になりますよ」ということを図にして表したものです。つまり、化粧前の顔(\(xの値\))に対して、化粧後の顔(\(y\)の値)がどうであるかを表した一覧。

例えば、上の図は、\(x=1\)に対して、\(y=3x\)というメイクをしてやると(メイクの仕方=関数の式は右上に書いてあります)\(y=3\)に、\(x=2\)に対してそれをすると、\(y=6\)になるということがわかる。打ってある一つ一つの点のことを数学では「座標」と言います。そして、このような図をかくことを「グラフを描く」(文字ではないので「書く」ではなく「描く」です)というわけです。
山の斜面とグラフ
ところで、上の、\(y=3x\)のグラフは、真っ直ぐ右上に登っていく線になっています。一次関数の直線は、つねに「右上がり、あるいは右下がりの直線である」という特徴があります。それはなぜかを次に見ていきましょう。
今度は、「山」について考えてみましょう。山を登っていると「急だな」というときと、「ゆるい道だな」というときとがあります。このときの違いは、(あえて言葉にしてみるのならば)「同じだけ歩くのに、一気に上に上がる(下に下がる)かどうか」ということではないでしょうか。「ずっと急な道が続く」というのは、「同じだけ歩くのに、上に上がる具合が大きいままである」ということでしょう。そして、このような道のゆるさ急さは、「傾き」と呼んでみることができます。一気に傾きが大きくなった(=急になった)とかね。

左側の斜面は、右側の斜面よりも「傾き」が大きいですね
一次関数のグラフの直線は、ちょうどこの山のように考えることができます。私たちは、横の方向に歩くので「(山の)傾きが急である」とは、「横に進むのに、一気に上に上がる」ということですが、この仕方で、数学でも「傾き」(この言い方を数学でもします)を考える。
上のグラフを見ながら考えると、傾きは「\(x\)(横方向)が\(1\)進むのに\(y\)(上方向)がいくつ大きくなるか」であり、この場合は、\(3\)であるということができます。そして、一次関数のグラフでは、常に傾きは一定(急なら急なまんま)です。
この3という数字、グラフの元になっている式にも出てきますね。\(x\)の前についている数。「傾き」がこれに一致するのはなぜでしょう?
こう考えることができるでしょう。もともと、例えば\(x\)が\(5\)だったとする。この時\(y\)は\(3×5=15\)です。\(x\)が\(1\)大きくなることは\(5+1\)と表現できますから、この時の\(y\)をあらたに計算しようとすると、式は\(3×(5+1)\)となります。これは、\(3×5+3×1\)に等しい(分配法則)ので、ちょうど、xが1増えると3だけ増えるわけです。\(y=◯x\)という式の傾きはいつも、◯です。
メイクに「ちょい足し」する——「y切片」、「平行移動」について
この記事の最初に考えようとしていた、問題の(2)は「\(y=-2x+8\)のグラフをかけ」というものでした。この問題だと、今見てきた\(y=◯x\)という部分の他にさらにおまけがついている。「\(+8\)」というヤツです。これはなんでしょう。
このことを考えるのには、まず、今までやったことから描ける\(y=-2x\)のグラフを考えてみるといい。
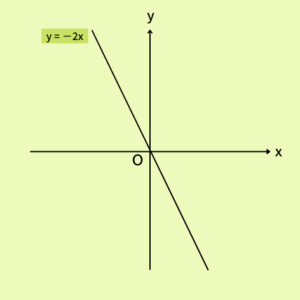
\(y=-2x+8\)の時、それぞれの\(x\)に対して、\(y\)はどのようになるでしょう。考えてみると、いつでも\(y=-2x\)の値に\(8\)足したものだと(メイクに、アイシャドウとか、「ちょい足し」したものだと)考えることができます。なぜかって、足し算は掛け算の後にするものだから、いつでも、\(-2×(xの値)\)という計算をしてから後ろの値を足してやるからです。したがって、グラフはこのようになる。
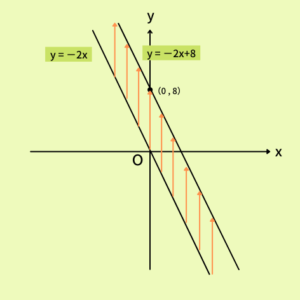
「\(+◯\)」という数字は、このように、「常に◯足される」(グラフで言えば、\(6\)だけ上に「平行移動」する)ということを表しています。\(x\)が\(0\)の時、\(y\)の値は\(0\)に\(+◯\)した数(\(y=-2x+8\)なら、\(0+8=8\))を取りますから、グラフでも\(x\)が\(0\)の時(=ちょうど、上向きの矢印(「y軸」と言います)と重なる時)、この◯という数を取る。このことを数学では「グラフがy軸を切る」と考えて「y切片」という言い方をします。
グラフによって切られたy軸、ちょうど竹が切られているように見えませんか?
節のまとめ
ここまでのことをまとめてみましょう。
\(y=-2x+8\)という式について、
\(-2\)の部分は「傾き」と呼ばれる。\(x\)が\(1\)大きくなると、\(y\)は、この傾きの分だけ大きくなる。
\(+8\)の部分は「y切片」と呼ばれる。\(x=0\)のとき(=「y軸」上にあるとき)、\(y\)の値はこの切片の値に等しい。
(2)を解く
これらの知識を使えば、記事の最初の問題は次のように解くことができます。
問題
(2)\(y=-2x+8\)のグラフを描け。
①最初にy切片(後ろの\(+8\)の部分)から、\(x=0\)の時の点を打つ。
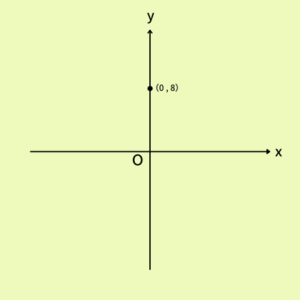
②傾き(\(-2x\)の「\(-2\)」の部分)を考えて、\(x=1\)の時に傾きの分だけ大きくなるように線を引き、一次関数では、その傾き(山の急ぐあい)は一定なので、それをどんどん上と下に伸ばす。

まとめ
本記事では、ある値について、それを代入し(メイク室のドレッサーに座らせ)、操作し(化粧してやり)、一つの値を出す式を数学では「関数」と呼ぶことを説明しました。そして、その代入する値と、結果として出てくる値とを対応づけた図としての「グラフ」について、「傾き」と「y切片」というものがあるのだということを説明しました。この二点を押さえることで、グラフが描けるようになるはずです。
数学は、出てくる用語一つ一つについてしっかりと理解を積み上げていくことが本当に大事です。「問題が解けない」のは、ほとんどの場合、そこで使われている言葉を理解していないからです。理解を積み上げる方法として、数学での考え方をそのまま勉強するのもアリですが、「別に数学なんて試験を乗り切ってしまえばいいのだ」というならこうやって勉強してもいいでしょう。
「関数」「グラフ」といった無味乾燥なものが、本記事の例えから、少しでも身近なものになってくれれば嬉しいです!
(ライター:菊池)
おすすめ記事
参考
東京大学文科III類出身、現在は哲学系の学科にいます。
数学の記事のほか、専攻に近づけて「勉強論」みたいなこともこれから書いていきたいと思っています。
読書のほか、昔のアメリカ・フランス映画を観たり、料理したりするのが好きです。いつの間にかつまらなくなった勉強の中に、新しいことを知ったり、できるようになった時のうれしい気持ちが戻ってくるような記事を書きたいです!











