この記事では、小学生のときにやったことのある「たし算」「ひき算」「かけ算」「わり算」について、マイナスのついた数、「負の数」が出てきた場合に、どうやってできるのかということを扱います。そのほか「累乗」という新たな考え方も扱います(そんなに難しくありません)。
まず最初に「負の数」というものが、どうやって考えることができたのか確認した上で、一つ一つの計算の考え方を見ていきましょう。
そもそも「負の数」ってどうやって考えたのだっけ……?
以前の記事では、数に関して「ものの個数」で考えるのではなく、「向き」と「大きさ」とから考えることで、「負の数」といったものを考えられるようになるということを扱いました。
東から10という強さの風が吹いてくることを「\(+10\)」というのならば、西からもう少し弱い、8という強さの風が吹くことは「\(-8\)」のように言えるのです。
このことを「風」という仕方ではなく、もっといろんな場合に言えるようにした、数学の図が「数直線」というものでした。
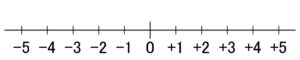
数直線の右側を+として、一つ隣の目盛りにいくことを「\(1\)」と決めたのならば、「三つ右の目盛りに行くこと」は「\(+3\)」、「四つ左の目盛りに行くこと」は「\(-4\)」と言えたのです(じゃあ、「\(+8\)」というのはどのようなことでしょう?)
負の数を含むたし算
「たし算」の新しい呼び方
まず最初に「たし算」のことをもっとカッコよくいう言い方を覚えましょう。「たし算」を、中学生以上の人がかっこよくいうときの言い方として「加法」というのがあります。そして、その結果を「和」と言います。
「足す」ことは、「加える」という仕方でいうこともできるでしょう。そして、そのことを、計算のルール・規則・法則のように考えるので「法」という語が付けられるのです。
また、その結果が「和」と呼ばれるのは、この漢字に「複数の別々のものが仲良くなる」という意味があるからだと考えられます。3と2という数がバラバラにあるのならば、この二つの数同士は、全く関係ない二つの数だと言えます。ここに「加法」ということをしたとき(つまり3+2という計算をしたとき)、この関係なかった二数は、急にくっつくことを命じられます。くっついて、仲良くなって、一体になって、それで5になる。こうした考え方が、加法の結果を「和」というときにはこめられていると、考えることができます。では、実際に加法を負の数でどう考えるかをみていきましょう。
「ものの個数」では考えられない!
みなさんは、今まで加法をものの個数で考えてきたのではないでしょうか? つまり、\(3+1\)だったら「三個のみかんがあるときに、さらにみかんを一個買い足してきて…」みたいに考えていたのではないでしょうか?
ですが、前回見たように、負の数は、数をものの個数と見る見方では考えられません。例えば、3に負の数-1を加える計算を考えるとき「3個のみかんがあるときに」みたいに考えると、-1個のみかんというものを考えることになってしまいますが、こんなものはありません(腐ったみかんだって、1個のみかんです)。

大昔のドラマに「腐ったみかんは周りを腐らせる」というセリフがありました。この時は、問答無用で「腐ったみかんが1, 2, 3, 4, 5個」と数えられますね。
じゃあ、どのように考えるか? 足し算(加法)とはそもそも何だったかを考え直して、そこから、それを「向き」「大きさ」の考え方で見直すとどうなるかというふうに考えてみましょう。
「加法」とはなんだろう?
まずは、ものを数えるというところから考えてみます。目の前にみかんがいっぱいある。みかんを1, 2, 3, 4, 5と数えていくとして、4個数えた時に、もう一個あった、だから、5というふうに数えられる。4+1=5という式は、このことを表現しているのです。4個ものがある時に、さらに1個、ものがあると、それは、5というものになるのだということです。
このことを、3個あった時、さらに2個あったという見方で見ると3+2=5という式が出てきます。2個あったとき、さらに3個あったという見方をすれば、2+3=5ということになります。足し算(加法)というのは、このようにして「◯個あるのと、△個あるのとを合わせて数えると、何個になりますか?」ということを数学で表現した形と言えるのです。
だとすれば、これを、ものの個数ではなく「向き」と「大きさ」を持ったものを「合わせる」と考えると、どのようになるでしょうか。
例えば、\(2+3\)という計算は、「「右へ2個進むこと」と、「右へ3個進むこと」とを合わせると、「どちらへいくつ」進んだということになりますか」という質問なのです。これは、右に2目盛り進んだ後に、さらに右へ3目盛り進めばいい。それは、右に5目盛りすすむということなので、\(2+3=5\)なのです。
この考え方をすれば、負の数について考えることもできます。「\(3+(-1)\)」という計算は、「右へ3行く」ということと「左へ1行く」ということを合わせるとどうなりますかということになります。これをやってみると、右に3いって、それとともに、左へ1行くということをしたことになりますから、これは「右へ2行く」ということになります。だから答えは2なのです。
同じことは「つな引き」のようにも考えられます。「\(3+2\)」という式は「右に3行く」ということをした上に、それに合わせてさらに、「右へ2行く」ということをするとどうなるかということですが、これは、+である(=同じ、「右に進む」チームにいる)二つの大きさを合わせることなので、「右へ(3+2)進むこと」と考えられるのです。あるいは、「\(3+(-2)\)」という式では、「右へ3進む」と、「左へ2進む」ということの衝突が起きます。左に2進もうとする力はここでは、右に3進むという力に負けてしまうでしょう。それでも完全に負ける(=右へ3進まれてしまう)ということはなく、進もうとする力のうち、2は打ち消されて、右へは1進むということだけが起きるのです。このことは「+(3-2)」という仕方で考えられます。
このことから、次のような性質が言えます。
x, yを正の数として、 \(x+(-y) =x-y\)
これは、「負の数の加法は引き算になる」というよくわからない話ではなく、3だけ右に進む力と、2だけ左に進む力があるならば、結局のところ\(3-2=1\)だけつなは右に進むのだ、ということを言っているのです。

地域の伝統行事で綱引きをする地域では、男女対抗で綱引きをする事があります。女性チームが勝つことも結構あるみたいですよ。
まとめ
たし算のことを「加法」と呼び、その結果は「和」と呼ばれる。
負の数の加法は「向き」「大きさ」で考える必要がある。「ある向きにある大きさだけ進むこと」と、「別の向きに、別の大きさだけ進むこと」とを合わせることで、数直線を使って足し算は考えられる。
また、そのような足し算は、「二つの向きに、それぞれの大きさ分働く力のつな引き」とも考えられる。この時、以下の公式が成り立つ。
\(x+(-y)=x-y\)
負の数を含むひき算
「ひき算」の新しい呼び方
ひき算のことは「減法」と呼びます。これは、元々の数から、新たに数を減らすからです。この結果のことは「差」と呼びます。この漢字は、例えば「今の彼氏と、昔の彼氏の差は…」と言うときのように、二つのものの「違い」を意味しています。数学では、全く同じ数を引けば、その答えは0になりますが、違う数を引いた時に出てくるのは、「引ききれなかった分」あるいは「引き過ぎてしまった分」としての、「違い」なのです。そのため、この漢字が使われているのです。

最初は「前の人と全く違う!」と思っていても、後から「やっぱ全然変わらないな…」となることだってあります。自分が変わらないと選び方のクセも変わらないんですよね。
「減法」とはなんだろう?
減法もものの個数で考えてはいけません。つまり、8個のみかんから、6個を取り去ると考えてはいけないのです。では、減法とはなんなのでしょうか?
それは、先ほど、減法の結果を「差」と言うのだといった時に示したような「違い」を求める計算なのです。例えば\(7-3\)という計算は「7と3とでは、いくつ数が違っていますか?」「7は3より、いくつ大きいですか?」ということを求める計算なのです。
このことを、負の数を考えられるような「向き」「大きさ」の考え方で考えるとどうなるでしょうか?
例えば、7-3は、「右に7進むことと、右に3進むこととではどう違っていますか?」「右に7進むことは、右に3進むことより、いくつ進んでいますか」となるのです。答えは「右に4だけ進んでいます」でしょう。したがって、\(7-3=4\)なのです。
負の数を引く場合も考えてみましょう。
\(5-(-2)\)は「右に5進むことは、左に2進むことより、いくつ進んでいますか」なのです。
これは、次のように考えてみましょう。
右に5進むことは、0からみてみるならば、右に5だけ進んでいます。そして、0よりさらに左に2進んでいる(-2)から見れば、それは、右に7だけ進んでいるということができると思います。したがって、\(5-(-2)=7\)なのです。
このことから、また性質が出てきます。
\(x-(-y)=x+y\)どういうことでしょうか。考えるのには、「\(x-0\)」という式と比べてみるとわかりやすいでしょう。
「\(x-0\)」という式は「xと0とでは、どれだけ数が違っていますか?」という式ですから、当たり前に「xです」ということができます。
一方、この式では、0よりさらに遠くの-yという数を基準にして「どれだけ違っていますか」と聞いているのです。だとすれば、「xだけではなく、さらにyぶんだけ離れているので、\(x+y\)です」ということになるでしょう。「負の数の減法は加法に等しい」というよくわからない話は、このようにして理解できます。
まとめ
「引き算」のことを「減法」と呼び、その結果は「差」と呼ばれる。
減法は、「ある向きにある大きさだけ進むこと」と「別の向きに別の大きさだけ進むこと」との違いを考える計算だとみることができる。
\(-y\)を引く減法は、もとの数から0までの違いに対して、さらにyだけ違っている分を加えると考えることができる。このことから以下の公式が成り立つ。
\(x-(-y)=x+y\)負の数を含むかけ算
「かけ算」の新しい呼び方
かけ算のことは「乗法」と呼びます。
このことは、どうしてそう呼ばれるかはっきりしないのですが、昔、戦争で使うための馬車(シンデレラのようなものではなく、乗って弓を引いたのでしょう)を走らせるためにつけた四匹の馬を「一乗」といったそうですからそこからきているのでしょう。この呼び方では二乗といえば\(4×2=8\)、三乗といえば\(4×3=12\)のようになります(この記事で最後に扱うように、数学でも、これから二乗、三乗という語が出てきますが、それはここで言われている計算とは違う計算なので注意してください)。
掛け算の結果は「積」と呼ばれます。
これもまた、はっきりしませんが、同じ数を一つのまとまりとして積み上げると考えることができるでしょう。「\(3×4\)」ならば、3というまとまりを4回積み上げているのです(\(3×4=3+3+3+3\)だったことを思い出しましょう)。
「乗法」とはなんだろう?
乗法についても、数直線で考えます。元々、掛け算は、例えば3×4なら「3個のものが4セットあれば、いくつになりますか」という計算だったと言えます。同じことを「個」の代わりに「向き」「大きさ」で考えてみるとどうなるでしょうか。
これは、「右に3進むということを、4セット(=回)やるとどうなりますか?」ということと一致するでしょう。したがって「右に12進む」ということで、12となるのです。
負の数についてやるならばどうなるでしょう。例えば、\((-3)×2\)という式は「左へ3進むということを、2セットやるとどうなりますか?」ということを表していると言えます。したがって、これは、左へ6進む、つまり、\(-6\)なのです。

ここでの「セット」は、「25mを3セット」などという時のイメージです。
マイナスは「元々の向きに対して逆向き」とも考えられる
しかし、\(3×(-2)\)という式はどうでしょう? ここでは、「右に3進むということを、(-2)セットやるとどうなりますか?」という訳のわからない文章になってしまうのではないでしょうか。
これについては、前の記事で見たように、マイナスを「元々の向きに対して逆向き」と考えるとうまく行くと思います。つまり、この式は「右に3進むということを、逆の向きに、2セットやるとどうなりますか?」という文だと理解することができます。
同じようにしてみれば、\((-8)×(-4)\)のような、負の数と負の数をかける式も理解できます。これは、「左に8進むということを、逆の向きに、4セットやるとどうなりますか?」なのです。したがって、32だけ、右の方向に進むことになりますから、答えは\(32\)となるのです。
このことは次のような性質にまとめられます。
\((+x)×(+y)=+(x×y)\)
\((-x)×(+y)=-(x×y)\)
\((+x)×(-y)=-(x×y)\)
\((-x)×(-y)=+(x×y)\)
例えば、最初の式であるならば、「右向きへ\(x\)進むということを、同じ向きに\(y\)繰り返すとどうなりますか」という式は、「右向きに\(x×y\)だけ進むことと同じです」と言っているのです。
まとめ
かけ算のことを「乗法」と呼び、その結果は「積」と呼ばれる。
乗法は、「ある向き、ある大きさへ進むこと」を、ある回数だけ繰り返すことと考えられる。ただし、繰り返す回数(=後ろにかけている数)が負の時には、それを「逆の方向に」繰り返すと考えることが必要である。
このことから、以下の公式が成り立つ。
\((+x)×(+y)=+(x×y)\)
\((-x)×(+y)=-(x×y)\)
\((+x)×(-y)=-(x×y)\)
\((-x)×(-y)=+(x×y)\)
負の数を含むわり算
「わり算」の新しい呼び方
割り算のことは「除法」と呼びます。
これもまた、由来のわからないところですが、「除」という字は、「のぞく」と読むのですから「そこから何が、ある数だけ取り除けますか」ということだと言えるのではないでしょうか。たとえば、「\(8÷2=4\)」という式は、「8からは何が、2人分取り除けますか」という質問に対して、「4が2人分取り除けます」と答えていると言えます。だから、8個のドーナツを二人で分けるのなら、4個ずつだということになるのです。
また、「除法」の結果は「商」と呼ばれます。
この字は「商売」の「商」ですが、元々は、価値をはかるという意味でした。除法は「8は4が2人分ある数である」というふうに、ある数に対して測定をしているとみることもできますから、そのためにこの漢字が使われていると考えられます。
「除法」とはなんだろう?
除法について負の数の場合を考える前に、そもそも、わり算とはどういうものだったかを考えてみましょう。
「\(7÷6\)」という計算には、二つの答え方がありました。「1あまり1」というものと、「7/6(あるいは1と1/6)」というものです。
一つ目の方は理解しやすいでしょう。「7個のものを、6人で分けるのなら、何個ずつになりますか?」→「1個ずつ取れますが、1余ります」という答え方です。
二つ目の答え方はなんなのでしょうか? それは、一つ目の答え方と何が違うのでしょうか?
ポイントは「分数」という考え方にあります。
「7/6」というのは、「7個のものを、6人分、ピッタリ分かれるように分けた大きさ」ということなのです。
上の式は、「7を6人分分けると1人分はいくらですか?」という質問に対して「6人分分けたときピッタリ分かれるようにしたときの、ちょうどその分です」と答えているのですから、違いようがありません。また、この場合、一つ目の答え方と違って、余りは全くありません。余っているものまで、ぴったり分けてしまっているのですから(この見方をするとき、1と1/6という帯分数が役立ちます。ここに出てくる1/6というのは「余った1個のものをさらに6人分に分けた」ということなのです)。
そして、負の数を含めて「除法」を考えるときには、まずは、この後者の答え方、分数を使って余りをなくす答え方の方で考えていきます。
分数を使ったこの考え方では、7÷6と7×1/6は等しいのでした。これも、言葉で考えてみれば難しいことはありません。「7を6人分分けると1人分はいくらですか?」という質問に対して、7×1/6という式は、「7を1/6回分だけ繰り返したものです」(=ちょうど6人分合わせれば、7になる、そのうち1回分だけ繰り返したものです)と答えているのですから、成り立つに決まっているのです。
6に対して1/6を、あるいは3に対して1/3を、2/3に対して3/2を、中学校の数学では逆数と呼びます。逆数とは、符号をそのままにして、分母と分子を入れ替えた数(元の数が分数でないときは、分母を1だと考えて、入れ替えた数)のことと言えます。したがって、「除法は逆数の乗法である」ということになります。
例えば、\(8÷2/3\)という式は、「逆数の乗法」である8×3/2に等しい。よって、\(12\)となります。
負の数の除法については、この「逆数の乗法に等しい」ということから考えることができます。
\(10÷(-2)\)という式は「10個のものを-2人分わける」なんて考えてもうまくいきません(-2人というのは、ゾンビでしょうか…)。そうではなく、\(10×(-1/2)\)のこと、つまり「右方向に10進むを、逆の方向に、1/2だけ繰り返したもの」であって、これは「左方向に5進む」-5となるのです。
まとめ
わり算のことを「除法」と呼び、その結果は「商」と呼ばれる。
ある数の分母と分子を入れ替えた数を「逆数」と呼ぶが、この呼び方を使って、除法は、逆数の乗法とみる事ができる。
例えば「÷◯」というのは、「×1/◯」に等しく、それは「○が正の時は同じ方向に、負の時は逆の方向に、1/◯だけ繰り返す」計算だと言える。
累乗
加法、減法、乗法、除法のほかに、新しく覚えることとして「累乗」というものがあります。
「累乗」とはなんだろう?
「累」という字は「重ねる」という意味を持っていますから、この計算は「重ねてかける」ということを表しています。何を「重ねる」のかというと、自分と同じ数を重ねるのです。
例えば、\(4×4\)や、\(4×4×4\)、\(6×6×6×6\)などといった計算が、この累乗の計算と呼ばれます。
それぞれの計算式は、掛け合わされる数の個数(\(4×4×4\)なら3個)を、4の右上に小さく書き添えることで表現することができます。
\(4^3\)
この小さい数のことは「指数」と呼び、また、こう表記した数を「4の3乗」というふうに呼びます。
ところで、このように右上に小さい数を書き添えることを今までした事がありませんか?
そう(思い出せたかな……?)、これは「面積」「体積」を考える時に単位の「cm」などに書き添えたものと同じ意味を持った添え字なのです(なんでそうなのかは、省略します……)! したがって「2乗」のことは「平方」、「3乗」のことは「立法」とも呼びます。
一問、練習してみましょう。\((-5)^5\)を解いてみます。
\((-5)^5\)
\(=(-5)×(-5)×(-5)×(-5)×(-5)\)
\(=(+25)×(-5)×(-5)×(-5)\)
\(=(-125)×(-5)×(-5)\)
\(=(+625)×(-5)\)
\(=-3125\)
まとめ
自分自身と同じ数をかける計算のことを「累乗」と呼ぶ。この計算式は、例えば、\(8^2\)のように表記できて、この時、右上に添えられている字を「指数」と呼ぶ。
二乗、三乗の計算は、それぞれ「平方」「立法」と呼ぶこともある。
(ライター:菊池)
おすすめ記事
参考
- 『新漢語林 第二版』
- 『四訂版 中高一貫教育をサポートする 体系数学1 代数編』
- 橋本治『いちばんさいしょの算数 ①たし算とかけ算』
- 橋本治『いちばんさいしょの算数 ②わり算とひき算』
- 守谷悦郎「和ってなに?積ってなに? いろんな和と積:どこが同じで、どこが違う」
- いらすとや
東京大学文科III類出身、現在は哲学系の学科にいます。
数学の記事のほか、専攻に近づけて「勉強論」みたいなこともこれから書いていきたいと思っています。
読書のほか、昔のアメリカ・フランス映画を観たり、料理したりするのが好きです。いつの間にかつまらなくなった勉強の中に、新しいことを知ったり、できるようになった時のうれしい気持ちが戻ってくるような記事を書きたいです!










