(5)仕事算
問題:ある会社には毎朝一定の量の仕事が入ってきます。いくらか仕事が溜まった状態から12人で仕事をするとちょうど15日で仕事がなくなります。同じ量の仕事が溜まった状態から15人で仕事をするとちょうど6日で仕事がなくなります。朝入ってきた分の仕事を当日に終わらせるには□人必要です。
元々溜まっていた仕事量を☆、1日に溜まる仕事の量を△、1人が1日でこなすことの出来る仕事量を◯としましょう。(問題を解いていく過程で分かることですが、実は元々溜まっていた仕事量については使いませんので、敢えて何かで置換する必要はありません)
- 12人で15日かかった場合
- 増えた仕事量; \(△ \times 15\)
- 全体の仕事量; \(◯ \times 12 \times 15=☆+△ \times 15\)
- 15人で6日かかった場合
- 増えた仕事量; \(△ \times 6\)
- 全体の仕事量; \(◯ \times 15 \times 6=☆+△ \times 6\)
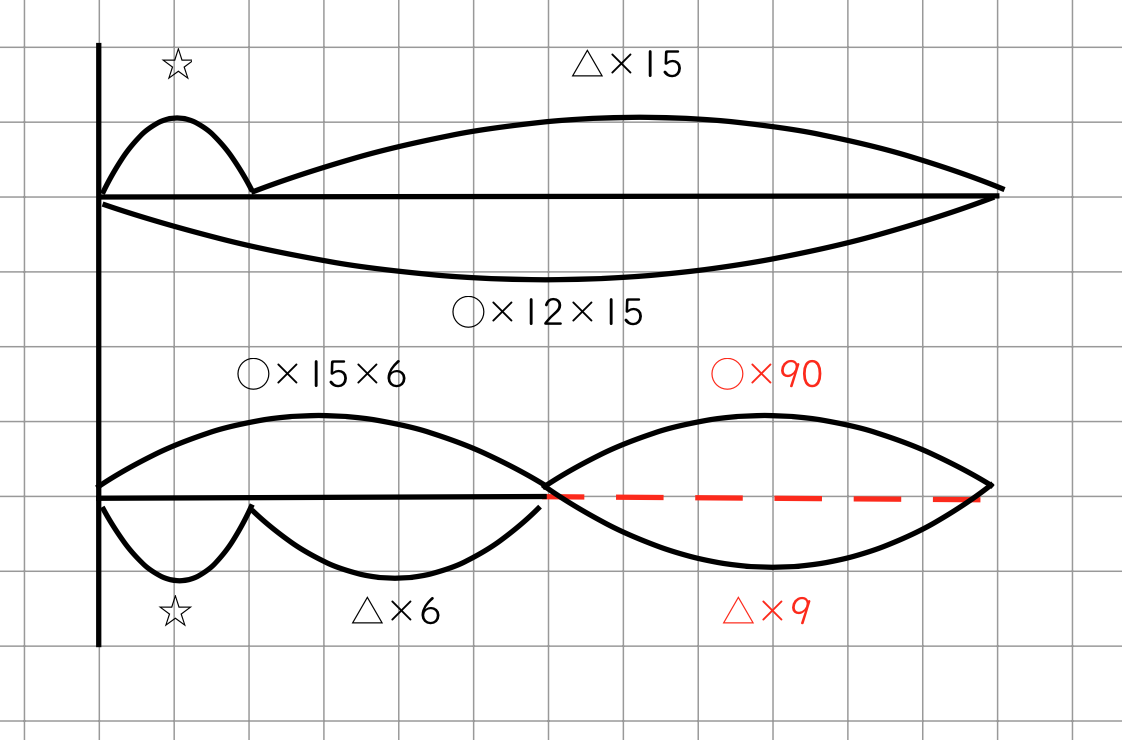
ここで両者を比べると、線分図の赤い点線の部分が2通りの式で表すことができ、
\(◯ \times 12 \times 15-○ \times 15 \times 6=△ \times 15-△ \times 6\)
\(◯ \times 90=△ \times 9\)
◯の90個分と△の9個分が等しいことがわかるので、△と◯の関係式は、
\(△=◯ \times 10\)
となります。ここで、△は”1日に溜まる仕事量”を、◯は”1人が1日でこなすことの出来る仕事量”をそれぞれ表しているので、朝入ってきた仕事△を、当日中に終わらせるには○10個分の仕事が必要とわかり、その仕事に必要な人数は10人とわかります。
答え:□=10
(仕事算についてはこちらの記事を参照のこと)
おすすめ記事
- 中学受験に出てくる仕事算ってどういうもの?無料プリント作ってみた
- つまずきやすい「仕事算」の解き方
- 人数が増えても2ステップで解ける!「仕事算」の解き方
- 線分図を活かそう!「ニュートン算」の簡単な解説