本記事は今年2021年度の1月校の入試について,いくつかの中学校の算数の問題を比較し,トレンドや出題傾向についてまとめたものです。
大手集団塾の模試や組分けテストなどが増えるこの時期、出題される問題の予測に役立つでしょうし,来年実際に1月校を受験される方にとっても,似た問題が出題される可能性があることから,傾向の把握は重要だと言えるでしょう。
いくつかの中学校を比較したところ4つの特徴がみられたため,それぞれについて対策法とともにご紹介していきます。
特徴① 余りのある計算
まずひとつめの出題の特徴として,足し算・引き算・掛け算・割り算という四則演算に関する出題が目立つ,ということが挙げられます。これはおそらくどの年度のどの学校も小問集合の中で出されているとは思いますが,そのなかでも余りが関わっているものが多い印象です。例えば次のような問題が出題されています。
2021を割ると29あまる数は全部で何個あるでしょう。
(栄東中学校(2021),一部改題)
Aは2桁の整数で,A×Aを15で割ると1余ります。このようなAは全部で何個あるでしょう。
(灘中学校(2021),一部改題)
クリスマス会に参加した人にお菓子を配りました。予定では,1人あたりお菓子を4個ずつ配り,24個余るはずでした。ところが,実際には,予定していた人数の3倍の人が参加したため,1人あたり2個ずつ配ったところ,余ったお菓子は2個でした。用意したお菓子は全部で何個ですか。
(浦和明の星女子中学校(2021),一部改題)
しかしこのように余りに関連する問題はとりわけ珍しい問題でもなく,取ると有利になる問題ではなく,取れないと不利になる・周りと差をつけられてしまう問題と言えます。そのため2月の入試にも来年の入試にも出題される可能性は大いにあります。したがって解き方の理解と対策が不可欠です。
このような問題は,
割られる数=商×割る数+余り
という式に情報を当てはめ,わからないところを□でおくと,計算が進められます。このときに余りの方が割る数よりも数が小さいという性質にも注目しておく必要があります。例えば最初にご紹介した栄東中学校の問題では,
2021=(29より大きい割る数)×商+29
という計算式が成立します。したがって,
1992=(29より大きい割る数)×商
という式に書き換えられます。よってここで求められているのは1992を割り切れる数,つまりは約数の個数だとわかります。このように公式に従っていくことが,余りのある問題を解くコツになります。前述した通り余りの問題はどんな入試でも出題される可能性があるため,繰り返し演習しておきましょう。
特徴② くり抜かれた平面図形・空間図形
次の出題傾向として,平面図形・空間図形の問題より,くり抜かれた図形の面積や体積を求める問題がよくみられます。平面図形としては次のような図形が登場していました。
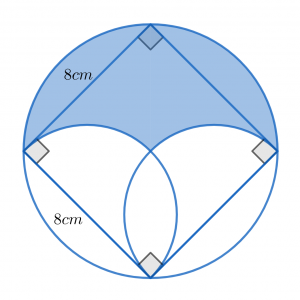
(浦和明の星女子中学校(2021),設問省略)
また空間図形の問題としては,次のようなものが登場していました。
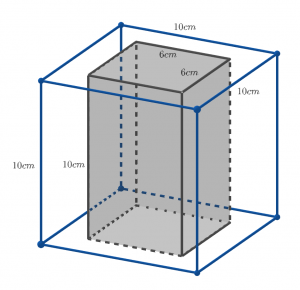
(西大和学園中学校(2021),設問省略)
このようなくり抜きをはじめとする,習った図形の組み合わせとしてある図形を捉えていくといった問題も,先ほどの四則演算同様に出題されやすいものです。したがって攻略は不可欠なものです。特にこの平面・空間の問題はつまずきやすいものであり,目が慣れていないと解き方が浮かんでこないという慣れが必要なものでもあるため,演習を積み重ねていく必要があるでしょう。
解き方のポイントとしては,図形の中に存在する図形を見極めることが大切です。例えば上の平面図形では円の中に正方形と半円2個が存在します。また下の空間図形では,立方体の中に直方体が存在します。このような登場した図形を図形同士の足し引きとして捉えていくということが攻略法になります。
平面図形も空間図形も中学受験では頻出な範囲なので,対策は必要です。この攻略のポイントを対策の参考にしてみてください。
特徴③ 仕事算
3つ目に取り上げる出題傾向は仕事算です。仕事算とは,仕事を進めるときのペースや効率について考えていく計算のことです。次のような問題が登場していました。
2つの印刷機A,Bがあります。Aの印刷機は印刷の速さについて2段階の速さが選べて,速い方は1分間で150枚,遅い方は1分間で50枚の印刷をすることができます。Bの印刷機は印刷の速さが一定で,1分間で100枚の印刷が可能です。印刷機は,トラブルがあると修理が終わるまで印刷できないものとします。
(西大和学園中学校(2021),設問省略)
ある仕事は,Aさんが12日間働いた後,Bさんが9日間働くと終わります。この仕事は,Aさんが8日間働いた後,Bさんが働いても終わります。また,Cさんが1人で働くと36日間で終わります。
(浦和明の星女子中学校(2021),設問省略)
このような仕事算は,全体を1として考えていくと計算しやすいです。そして印刷機A・印刷機B,またはAさん・Bさん・Cさんの1日の仕事量を,全体の仕事量のなかのどれだけを占めるかという割合として考え,線分図などに書き起こしていくと解き進めやすいでしょう。
この他にも仕事算以外にも中学受験ではたくさんの文章題が出題されますので,つるかめ算・旅人算といった基本的な問題及びその解き方も,本番までに抑えておきましょう。
特徴④ 条件の整理
最後にご紹介するトレンドは条件の整理に関する問題です。条件の整理とは,具体的な計算や数式があるわけではなく,ゲームやパズルのように与えられた条件をまとめ,その条件に従って数式や図表を読み取るという問題です。例えば次のような条件が出題されていました。
はじめ,3枚のカード①,②,③が左からこの順に並んでいます。これらのカードの並べ替えを何回かします。1回の並べ替えにつき,次の(A)~(D)のどれか1つが行われます。
(A)最も左にあるカードを右端に移動させる
(B)最も右にあるカードを左端に移動させる
(C)最も左にあるカードを残り2枚の間に移動させる
(D)最も右にあるカードを残り2枚の間に移動させる
(灘中学校(2021),設問省略)
この他にも,海陽中学校や西大和学園中学校で類似した問題が登場しています。
ただし,この傾向は1月受験校に難関校と言われる中学校が多いから表れているものでもあるため,お子様の受験校レベルに合わせた対策が必要となります。条件の整理がこれまで出ていない中学校を受験される場合は,この範囲の対策より図形や文章題の対策をする方が効果的です。
加えて条件の整理の問題は,周りの受験生もほとんど解けないでしょう。そのため対策の優先順位は低いです。受験生の半分は取れるかな,くらいのレベルの問題から仕上げていきましょう。この前提のもと,条件の整理の対策法をご紹介します。
まずは文章の読解能力,つまりは国語力を養うことが重要です。上の例題からもわかる通り,条件の整理の問題はそもそも情報量や文章量が多いです。したがって算数の問題を解くことではなく,本や新聞を読むことで間接的に力が養われるでしょう。
問題の攻略法としては,見えている条件をまとめて理解することです。今回の例題の条件はこれ以上簡単にはまとめられないでしょうから,理解できるようにいくつか例を考えていきましょう。
はじめに①,②,③という順番で並んでいるとして,(A)の場合は②,③,①となりますし,(B)の場合は③,①,②のようになります。このように具体例を考えていくことが有効です。
このようにわかっているところを確定させた後,わからないところを考えたり,計算のフェーズに移ったりしていきます。以上のポイントを抑えて演習や勉強を積み重ねていくと,条件の整理の問題で点を得ることができるようになるでしょう。
まとめ
本記事では1月受験校の問題の特徴をまとめ,それらの攻略法を解説していきました。分析の結果,上であげた①余りのある計算,②くり抜かれた図形,③仕事算,④条件の整理という特徴が見えてきました。春から新小6の方,またその保護者様にとってこれらの情報がお役に立てば幸いです。
おすすめ記事
参考
(ライター:大舘)
















