皆さんは「パスカルの原理」という言葉を聞いたことがあるでしょうか? 教科書によっては単に圧力の伝わり方の一例として紹介されているだけかもしれません。人によっては図を見たときに、「これもパスカルの原理をつかっているのか!」と納得するかもしれませんね。パスカルの原理を使った図はそれくらい特徴的な見た目をしています。このパスカル原理、圧力を理解する上では重要なことがらですが、その内容を詳しく考えたことがあるという人は少ないのではないでしょうか。
今回はそんなパスカルの原理も含めた、「圧力の伝わり方」について解説していきます! どんなこともただ暗記するだけではなく、自分の頭でしっかり納得してから学習を進めていくと、効率が上がります。
本記事では、以下のことを解説します。
- 力は物体の中を伝わって移動する
- 水や気体の中で、圧力の伝わり方はすべて同じ
- パスカルの原理とは液体や気体の圧力の伝わり方についての原理である
圧力について、まだ基礎が理解できていないという人は、過去の記事を参考にしてください!
「圧力は勉強したけど、完全に理解したわけではない……」という人でも理解できるように、詳しく解説していますので、ぜひ最後の問題まで解いて、理解を深めていってください。それでは解説していきます!

Contents
圧力の伝わり方に関する基本を理解しよう!
水の中で圧力はどのように伝わる?
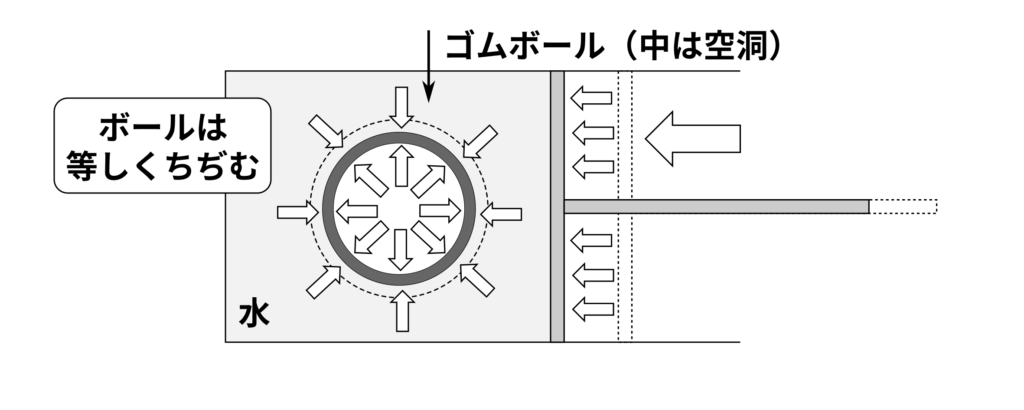
まず、力の伝わり方に関する基礎的な内容を説明します。次の図を見てください。筒の中に水が入っています。この筒の中に、中が空洞になっていてのびちぢみするゴムボールが入っています。水がもれないように密着させた取りつけると、図にあるような装置が完成します。
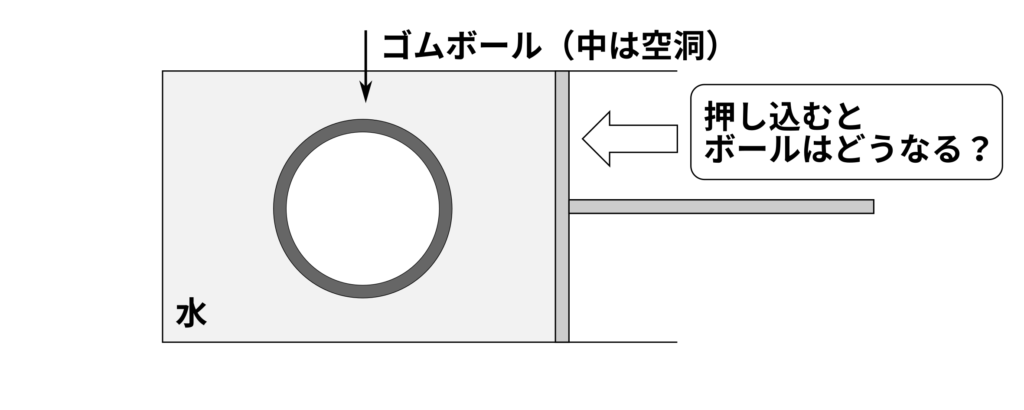
この装置の取っ手を動かしてみましょう。問題形式で考えてみてください。
問題
まずは取っ手を筒の中に押し込みます。このとき、ゴムボールはどのように変化するでしょうか。次の図の中から選んでください。
(1) ゴムボールは等しくちぢむ
(2) ゴムボールは横方向にちぢむ
(3) ゴムボールは縦方向にちぢむ
(4) ゴムボールは変わらない
解答
さて、答えがわかったでしょうか。答えを先に言ってしまうと、
(1)の「ゴムボールは等しくちぢむ」です。
なぜそうなるのかをこれから解説します。
この問題では、(2)と誤答した人がいるのではないでしょうか。なぜなら、我々が日常で目にする力のかかり方は、力をかける方向と平行だからです。ゴムボールを横方向から板で挟んで力をかけたら、ゴムボールは必ず横方向にちぢみますよね。
なぜ横にちぢむのかをもう少し詳しく考えてみましょう。いま、ボールに力を加えているのですが、直接力をかけているのではなく、板を通して力をかけています。そして、この板がボールを横方向から押すからこそ、ボールは横方向にちぢむのです。当たり前と思うかもしれませんが、板を通して間接的に力を加えているという点がポイントです。
次に、問題の状況を見てみましょう。ボールは手から直接力をかけられているでしょうか? それとも、板から力を受けているでしょうか。
もちろん、そのどちらからでもありません。ボールは水から力を受けているのです。この意味が分かるでしょうか。
水は板のように固体ではありません。水はボールの裏側にも上側にも回り込むことができます。その結果、水はボールをすべての方向から押しているのです!
ちょっと理解が追いつかないかもしれませんね。普段は意識することがないからこそ、自然界では当たり前のことでも、人間が納得するには苦労します。
ですが、よく考えてみれば、水も固体も同じだということがわかります。力のかけ方は同じなのです。違うのは、水が液体であり、変形しながら様々な方向に入り込むことができるという事実です。そこに力をかけるものがあれば、力をかけるということを覚えておきましょう。極端なことを言えば、もしボールを押す板がスライムのように自在に形を変えるものであれば、一方向からでなく、すべての方向からものに力をかけることも可能なのです。
「でも、手は水に触れていないのにすべての場所で水が力を加えるのはおかしい」と思った人もいるのではないでしょうか。もしかしたら、この点が一番納得いかないかもしれないですね。まるで力が水の中にワープしているかのようです。このことについてさらに解説します。
水の中で力が伝わるのはなぜ?
先ほど、板の例をあげましたよね。この板がボールを押すというのは理解しやすい話だと思います。しかし、よく考えてみてください。板がボールを押しているのは板の左側の面です。力をかけているのは右側です。ここでも水の中と同じように力がワープしているみたいですよね。このように、かけた力が物体の中で移動してほかの物体に影響をおよぼすというのは非常によくあることなのです。
もっと簡単に、板がボールを押している例をよく考えてみましょう。
このボールが変形するのは、ボールが板を押す力より、板がボールを押す力の方が大きいときです。ボールが変形しない程度の力でボールを押しているときは、ボールも同じ力で板を押しているので、ボールを変形させません。
もっと押す力を強くしてみましょう。ボールはゴム製なうえに、中に(大気圧しかない)空気を含んでいるので、板を押し返す力の限界は弱いです。このとき、ボールの右側は板から直接押されていて、内側にちぢみます。
ボールに起きる変化はこれだけではありません。ボールは反対側も同じだけ内側にちぢみます。左から力をかけているのに、なぜ右側にボールが変形するのでしょうか。
その理由は、ボールが板とは反対側の筒の底からも力を受けるからです。当たり前かと思うかもしれませんが、なぜなのかを考えてみましょう。
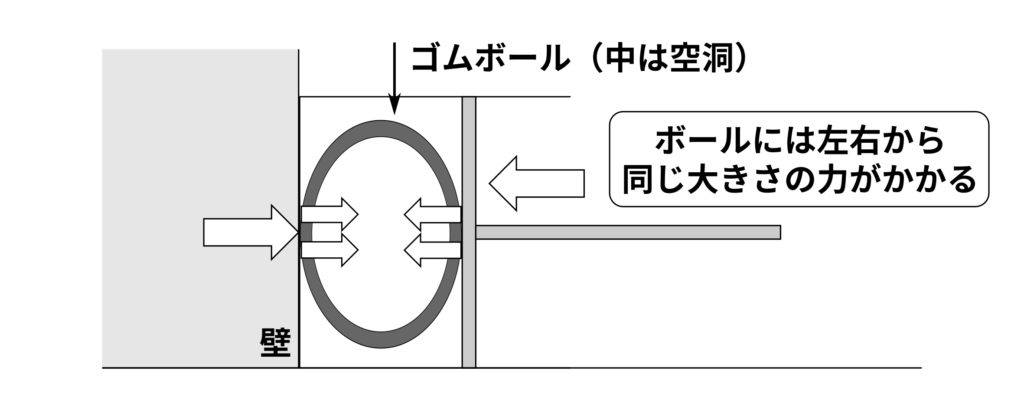
ボールにかけた力は、ただボールの左側から伝わるだけではありません。それは、ボールのゴムの部分などを通して反対側に移動します。そして、ボールの右側にかけたはずの力は、筒の底にも同じように力をかけます。
筒は壁によって固定されているとしましょう。壁は、筒から力をかけられます。力をかけられた壁は黙ってはいません。そのままだと左側に移動してしまうので、右側に同じように力をかけます。そしてこの力は筒を押し、さらに筒は中に入っているボールを押します。あとは板の場合と同じように、押し返す力の弱いボールがちぢむというわけです。
つまり、物体に力をかけると、力はその物体の中を移動します。ですが、物体が固定されている場合は、物体の内部にその力と大きさが同じで、向きが反対の力が加わります。結果的に物体の中の力は相殺されて、物体は動かないというわけです(少々不正確ですが、このような力を伝わり方を作用・反作用の法則といいます)。
さて、水の中の話に戻りましょう。板と筒の例から、力は物体の中を移動することがわかりました。力は、水の中でも同じように伝わります。先ほどから繰り返しているように、水は変形可能です。このとき、水は力を全方向からかけることができます。つまり、板の例では横方向にしか伝わらなかった力が、縦横斜めすべての方向に広がることになります。したがって、ゴムボールはすべての方向に関して押し返す力が弱いので、すべての向きに等しくちぢむというわけです。
空気も水と同じように考えればよい!
以上のことが、圧力の伝わり方に関する基礎的な内容です。さて、基礎がわかったところで、少し応用させてみましょう。
問題
先ほどと同じような筒を用意し、その中に(割れない)シャボン玉を入れます。空気がもれないように丁寧に作られた取っ手を動かして、筒の中の空気を押し込みます。このとき、ごくわずかですが、シャボン玉に空気の圧力が加わります。シャボン玉に加わる圧力の方向として正しいものを次の選択肢から選んでください。

(1) シャボン玉の取っ手に近い方から力を受ける
(2) シャボン玉の横方から等しく力を受ける
(3) シャボン玉の全方向から等しく力を受ける
(4) シャボン玉の縦方向から等しく力を受ける
解答
ここまで記事を読んできた人なら簡単ですね。
答えは(3)の「シャボン玉の全方向から等しく力を受ける」
です。空気も水と同じように、シャボン玉の全方向に力がかかります。筒の中は空気が充満しているので、シャボン玉に力を直接加えなくても、空気が力をかけてくれます。
パスカルの原理って何?
さて、圧力の伝わり方について理解したところで、パスカルの原理に移りましょう。
とはいっても、上の話でパスカルの原理についての解説は終わってるといってもいいでしょう。念のため簡潔にまとめると、
パスカルの原理
水や気体が容器の中に閉じ込められているとき、水や気体に伝わる圧力はすべての地点、方向で同じになる
となります。
パスカルの原理はまさに、水の中でボールが等しくちぢむことを説明していますね。もし筒の中にボールが入っていなくても、あるいはもっとたくさんのボールが入っていたり、筒の形が違っていたとしても、圧力はすべての場所で同じようにかかります。パスカルの原理によって、複雑な容器になっても難しく考える必要がなくなるということです。
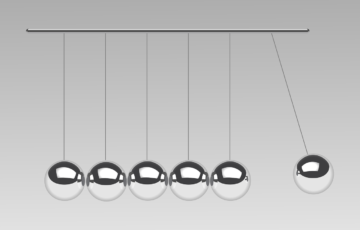
パスカルの原理の説明でよく使われるのは次のような図です。
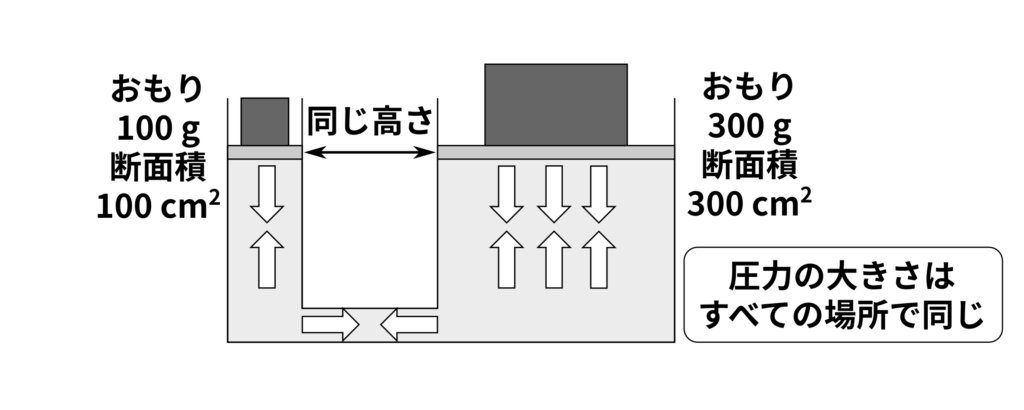
パスカルの原理の図のポイントは、「違う重さのおもりが同じ高さでつり合っている」ということです。
重いおもりの方が大きな面積の板の上に乗っているため、重いおもりと小さいおもりが板を通して水にかける圧力は同じです。
普通に考えれば、重いおもりの方がものを押す力が大きいので、「軽いおもりの方が高くなるのでは?」と思うかもしれませんが、そうはなりません。
もし高さが違えばどうなるでしょうか。おもりのかける圧力は2つで同じになっているので、高さが違えばその水の分だけ重さが大きくなり、左の容器の方が圧力が大きく、右のほうが圧力が小さいという状況になります。
水は静止しているので、容器のつなぎ目では圧力は同じのはずです。したがって、容器の中で、圧力の大きさが違うということになります。
しかし、実験によれば、このようなことはおこりません。板にかかる圧力を同じにした状態で、左の容器の板の方が高い状況を作り出すと、容器の中の水は移動し、同じ高さになって落ち着きます。右の容器が高い場合も同じです。これは、パスカルの原理が成り立っているということを意味します。
パスカルの原理をつかえば、「板の面積を小さくすれば、小さなおもりでも大きなおもりを支えることができる」ことが成り立ちます。
この、「重さの違うもの同士が、(容器など)力を伝えるものの形の違いを調整することによってつりあう」という性質は、てこの原理を用いた力のつり合いに似ています。昔の人は重機など持っていませんので、大きな建造物を作る際に、小さな力で大きなものを持ち上げるということが重要な問題でした。そのような過程で、てこの原理やパスカルの原理は同じように使われていたのだと想像することができます。
練習問題に挑戦!
さて、圧力の伝わりかたの知識をつかった練習問題に挑戦してみましょう!
問題
水の高さが同じでつりあっている次のような容器があります。右側のおもりの重さは\(300\,\mathrm{g}\)、おもりを支える板の断面積は\(300\,\mathrm{cm^2}\)です。左側のおもりの重さは\(100\,\mathrm{g}\)、板の断面積は\(100\,\mathrm{cm^2}\)です。
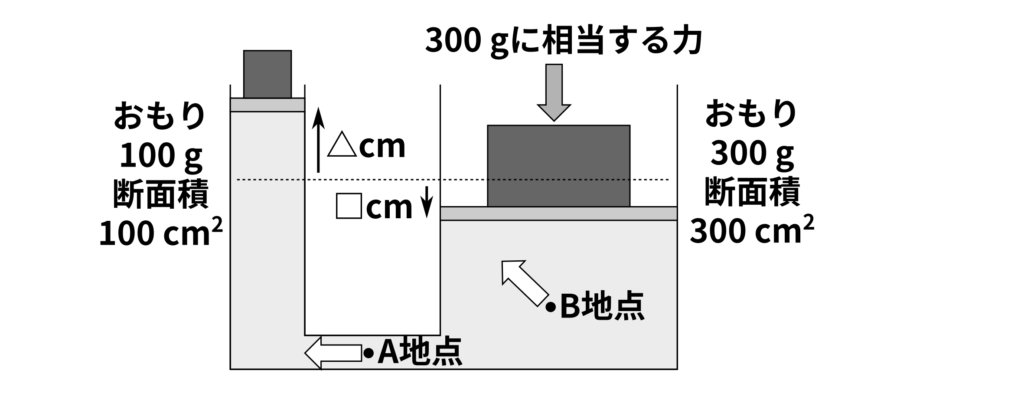
この容器の右側のおもりに、\(300\,\mathrm{g}\)の重さに相当する力を加えました。すると、右側の板とおもりは下がり、左側の板とおもりは上がりました。このとき、以下の問題に答えなさい。
(1) 右側の容器が下がった距離と、左側の容器が上がった距離をそれぞれ答えなさい。ただし、水は\(1\,\mathrm{cm^3}\)につき\(1\,\mathrm{g}\)とします。
(2) 図のA、B地点の矢印の方向にかかる力の大きさは\(1\,\mathrm{cm^2}\)あたり何\(\,\mathrm{g}\)に相当するかを答えなさい。
解答
(1) この問題は少し難しかったかもしれません。いくつかのステップがあるので、順番に解説していきましょう。
まず、解答の方針を考えましょう。ポイントは、容器の右側で減った水の体積と、容器の左側で増えた水の体積は同じということです。
つまり、左側で増えた水の体積がわかれば、それを板の断面積で割ると上がった板の距離がわかります。
水の体積は右側の容器にかけた力に影響されます。水は\(1\,\mathrm{cm^3}\)につき\(1\,\mathrm{g}\)なので、水の重さがわかれば体積がわかります。
右側の容器で減った水の重さは、右側の容器にかけた力に相当する重さと同じです。では、実際に計算してみましょう。
まず、右側の容器で減った水の重さを求めましょう。これは、右側の容器にかけた力に相当する重さに一致するので、
(右側の容器で減った水の重さ)=\(300\,\mathrm{g}\)
となります。次に、水の重さを体積に変換しましょう。これは、
(移動した水の体積)=\(300\,\mathrm{g} \div 1\,\mathrm{g} \times 1\,\mathrm{cm^3} = 300\,\mathrm{cm^3} \)
となります。最後に、これを左側の容器の板の面積で割れば求める距離が出てきます。これは、
(左側の板が上がった距離)=\(300\,\mathrm{cm^3} \div 100\,\mathrm{cm^2} = 3\,\mathrm{cm}\)
と求めることができます。
(2) この問題は、今回の記事の一番重要なことを聞いています。これまでの解説で
水や気体の中で、圧力の伝わり方はすべて同じ
ということを説明してきました。このことを使うと、AとBの圧力と、おもりが板にかける圧力は同じということになります。
おもりが板にかける圧力は右と左で同じで、
\(300\,\mathrm{g}\div 300\,\mathrm{cm^2} = 100\,\mathrm{g}\div 100\mathrm{cm^2} = 1 \mathrm{g\,/\,cm^2}\)
となります。したがって、答えはA、Bともに
\(1\,\mathrm{g}\)
と求めることができます。
ここで、右側の容器には\(300\,\mathrm{g}\)だけ余計な力がかかっているから、圧力は\( (300\,\mathrm{g} + 300\,\mathrm{g}) \div 300\,\mathrm{cm^2}\)になるのではないかと思った人もいるかもしれません。
ですが、右側の容器には左側の容器の水の体積が増えた分の重さがかかっています。この重さが、かけた力と相殺することになるので、差し引き\(300\,\mathrm{g} \div 300\,\mathrm{cm^2}\)だけの圧力がかかることになります。
最後に……の前に
『個別指導塾テスティー』の公式LINEにて、
『中学受験を9割成功に導く』メールマガジンを
毎週、完全無料で配信中✨
塾の活用の仕方・最適な勉強法・親として子供をどう教導するかの指針など 中学受験するお子様を持つ親御さんが知りたい知識を幅広くご紹介!!
↓↓詳細は以下をタップ↓↓

最後に
本記事では、「圧力の伝わり方」について解説しました! 記事の中で解説したように、水の中や気体の中を伝わる圧力は、普段目にする力とは少し違ったはたらきかたをするので注意しましょう。この記事を読んで「パスカルの原理とは何かがわかった!」という人が一人でも多くなると幸いです。圧力は決して中学入試で頻出の内容とは言えませんので、勉強する機会も少ないと思います。だからこそ、忘れたころに復習して、抜け目がないように準備しましょう! うれしいことに、圧力の問題では、そこまで複雑な問題はでてきませんので、基本的な内容をしっかり答えられるようにしましょう。それでは、引き続き中学受験理科の勉強を頑張ってください!