学校情報
応募状況
2020年度
| 年度 | 募集人員 | 応募者数 | 受験者数 | 合格者数 | 実質倍率 |
| 2020 | 235名 | 555名 | 532名 | 283名 | 1.9倍 |
2019年度
| 年度 | 募集人員 | 応募者数 | 受験者数 | 合格者数 | 実質倍率 |
| 2019 | 235名 | 529名 | 210名 | 296名 |
1.7倍 |
進路実績
2020年度卒業生:229名 表示形式:合格者数(現役合格者数)
| 東京大学 | 85名(71名) |
| 京都大学 | 2名(2名) |
| 一橋大学 | 3名(2名) |
| 東京工業大学 | 5名(4名) |
| 早稲田大学 | 136名(109名) |
| 慶應義塾大学 | 93名(72名) |
| 上智大学 | 39名(36名) |
| 東京理科大学 | 82名(49名) |
| 学習院大学 | 3名(3名) |
| 青山学院大学 | 8名(4名) |
| 立教大学 | 12名(9名) |
| 中央大学 | 34名(24名) |
| 法政大学 | 11名(6名) |
| 明治大学 | 70名(49名) |
| 医学部医学科(※)合計 | 126名(85名) |
※東京医科歯科大学、東京大学理科Ⅲ類、千葉大学、横浜市立大学、筑波大学、防衛医科大学、群馬大学、信州大学、東北大学、新潟大学、大阪大学、富山大学、浜松医科大学、慶應義塾大学、順天堂大学、東京慈恵会医科大学、国際医療福祉大学、日本医科大学、東邦大学、東京医科大学、日本大学、自治医科大学、獨協医科大学、杏林大学、昭和大学、聖マリアンナ医科大学、帝京大学、東北医科薬科大学
学校説明会日程(2019年度)
| 説明会 | 日程 | 場所 |
| 学校説明会 |
第1回 2019年10月30日(水)9:30〜12:00 第2回 2019年11月2日(土)9:30〜12:00 第3回 2019年11月9日(土)9:30〜12:00 第4回 2019年11月13日(水)9:30〜12:00 |
桜蔭中学校内講堂 |
入試情報(2020年度)
| 一般入試 | |
| 入試日 | 2020年2月1日(土) |
| 募集人員 | 合計235名程度 |
| 入試科目 |
①筆記試験(国語・算数・理科・社会) ②生徒面接 ③保護者面接 |
| 出願期間 | 2020年1月10日〜1月16日 |
| 合格発表 |
2020年2月2日9:00より掲示。 (8:40までに保護者同伴登校、※8:00より受付開始) |
基本データ
試験時間・満点
| 国語 | 算数 | 理科 | 社会 |
合計 |
|
| 試験時間 | 50分 | 50分 | 30分 | 30分 | − |
| 満点 | 100点 | 100点 | 60点 | 60点 | 320点 |
満点・合格者平均点・合格者最高点・合格者最低点
※点数は公表されていません。
問題構成
桜蔭中の算数は、試験時間50分に対して大問が4問、総設問数が10問程度となっています。ここ数年でこの傾向に変化は見られません。
大問4問のうち、2問は計算問題や応用小問といった基本〜標準レベルの問題で構成されているのに対し、残りの2問では応用問題が出題されています。
解答形式
問題用紙と解答用紙が別々に用意されており、ともにB4サイズです。
計算問題や応用小問の中には、答えのみを空欄内に書き込む問題もありますが、基本的には途中式や考え方についての記述を求める問題がほとんどです。そのため、答えが合っていても考え方や式の記述が不十分であった場合、十分な得点を期待できない可能性が高いため、注意が必要です。
近年の出題内容
2020年度
| 大問番号 | 分野・単元 |
| 大問1 | 計算問題・小問集合 |
| 大問2 | 辺の長さ、速さと比、体積、表面積 |
| 大問3 | 立体図形、相似比、体積、表面積 |
| 大問4 | 整数の性質、調べ上げ、つるかめ算 |
2019年度
| 大問番号 | 分野・単元 |
| 大問1 | 計算問題・小問集合 |
| 大問2 | 植木算、面積、辺の長さ、図形の移動 |
| 大問3 | 食塩水の濃度、つるかめ算 |
| 大問4 | 時計算 |
2018年度
| 大問番号 | 分野・単元 |
| 大問1 | 計算問題・小問集合 |
| 大問2 | 平面図形、場合の数 |
| 大問3 | 割合と比、売買損益 |
| 大問4 | 立体図形 |
出題傾向
概要
- 過去8年間の出題ランキング
- 1位:図形
- 2位:規則性
- 3位:速さ
- 4位:割合と比
- 5位:計算問題
- 大問ごとの出題傾向や難易度
桜蔭中学校の算数は、試験時間50分に対して大問が4問、総設問数が10問程度となっています。
全4問のうち、はじめの2問では計算問題・応用小問といった基本〜標準レベルの問題が出題されています。ここ最近は計算問題1〜2問+応用小問3〜4問程度が出題されることが多いです。計算問題は分数・少数・整数を中心とした基本的な問題であることがほとんどで、応用小問は毎年幅広い分野から、定型問題レベルの文章題が出題されています。
第3問以降の応用問題では、第1・2問の応用小問と比べて長めの文章題が出題されています。前半よりも全体的に難易度が高く、時間のかかる問題が多いです。
頻出分野は図形、規則性、速さ、数の性質、割合と比などで、複数の分野を組み合わせた複合的な問題もたびたび出題されています。解き方がすぐに思いつけば比較的速く解くことができますが、そうでないと大幅に時間を割いてしまうような問題が多いです。
計算ミスや問題文の読み間違いといったケアレスミスは、思わぬ失点や時間のロスにつながりかねません。十分に注意しましょう。
内容
出題分野・出題傾向についての詳細
第1問では、ここ数年で毎年必ず計算問題が出題されています。当校の計算問題は、分数・少数・整数を中心とした四則計算・逆算・計算の工夫などの基本的な問題がほとんどです。全体の中でも最も難易度が易しく設定されているため、必ず満点を目指したい内容となっています。
第1・2問では他にも小問集合を中心とした出題が見られます。応用小問では、各分野の文章題が出題されています。出題分野は幅広く、毎年趣向を変えて出題されています。ここ最近では、植木算・つるかめ算・長さ・面積・体積・調べ・条件の整理などがよく出題されています。
第3問・第4問の応用問題では、前半2問と比べると、分量が多めの文章題が出題されています。後半2問は図形分野からの出題がよく見られます。図形分野からは平面図形、立体図形問わず様々な種類の問題がまんべんなく出題されています。
なかでも角度、面積、長さ、辺の比と面積の比、相似、点の移動、平面図形の移動、回転体、体積、水の深さと体積などが頻出です。なかでも求積の問題は特に頻出で、しばしば数の性質や比と組み合わせた合成問題なども見られます。
図形のほかには、つるかめ算、速さ、規則性、場合の数などが頻出です。
つるかめ算は単体で出題されることもありますが、ここ最近では、「割合」と関連づけて解く問題が出題されています。
速さからは速さ・旅人算・通過算・速さと比が、規則性からは植木算、数列、周期算が頻出です。
また場合の数からは、調べ上げ・推理・条件の整理を伴う問題が出題されています。ここ最近では、手間のかかる数え上げを伴うような、面倒な問題もしばしば出題されています。
難易度について
まず前半2問についてですが、計算問題は基本的な分数・整数・少数の四則計算や逆算の問題がほとんどです。全問の中でも最も難易度が易しく、一番得点を期待しやすいと言えるでしょう。
応用小問は標準〜やや難レベルの問題で構成されていて、計算問題よりは難易度が高めに設定されているものの、後半2問の文章題と比べれば解きやすい問題となっています。
前半2問に関しては、難易度が高くないとは言っても、ほとんどの問題が一筋縄ではいかない場合が多いことが特徴的です。例えば、ほとんどの計算問題や応用小問では割り算の商にあまりが出てしまうことが多く、複雑な分数が答えになってしまうことが多々あります。
後半2問では応用問題が出題されています。応用問題は、前半よりも長めの文章題を中心に出題されており、前半と比較して難易度もぐっと上がります。定型問題レベルの問題はほとんど出題されておらず、発展的な思考力が必要となります。
一方で、いわゆる難問・奇問といった、高度なひらめきを必要とするような問題は出題されていません。あくまで単元についての理解度や、受験生の演習量がそのまま得点に直結するような内容となっていることが特徴的です。
後半2題は、解法さえ分かってしまえば順調に解けるものの、一度つまずいてしまったり迷ってしまうと、なかなか答えまでたどり着けなくなってしまうような問題が多いです。
前半2問と比べて後半2問は難易度が高くなるため、前半2問でどれだけ得点できるかが合格するためのカギとなります。
対策方法
分野別対策法
図形対策
桜蔭中の算数入試は、図形分野からの出題が多いです。角度・長さ・展開図・辺の比と面積の比・相似・面積・体積など、様々な種類の問題がまんべんなく出題されています。
そのなかでも、平面図形からは角度、面積、長さ、辺の比と面積の比、相似、点の移動、平面図形の移動が、立体図形からは回転体、体積、水の深さと体積などが頻出です。
また図形問題では、割合や比の考え方と組み合わせて解くことを求められる場合が多いです。図形対策と合わせて割合と比の対策も進めておくと良いでしょう。
まずはそれぞれの問題の典型的な解き方や公式を身につけるため、標準的なレベルの問題集をくり返し解いて、定型問題の解法を身につけましょう。定型問題が一通り解けるようになったら過去問研究に移り、実際に出題されている問題の難易度や特徴を理解しましょう。
桜蔭中の算数では、定型問題には見られないような複合的な図形や、工夫が必要な求積の問題が出題されています。過去問を数多くこなすことで、実践的な応用力を身につけましょう。
速さ対策
桜蔭中学校の算数では、速さの問題が頻出です。なかでも旅人算、速さと比の問題がよく出題されています。
対策方法についてですが、まずは標準的なレベルの問題集をくり返し解き、速さに関する定型問題の解法を一通り身につけましょう。定型問題を一通りマスターしたら過去問研究に移り、応用問題を解く上での実践的な力を身につけましょう。
旅人算の応用問題は、定型問題として出題される場合と比べて、図を描かないと状況が理解しづらいことがほとんどです。線分図やグラフを描くことで、条件をうまく整理することができます。普段問題を解くときから図を描く練習をするようにしましょう。
計算対策
ここ最近の入試では、毎年大問1で1問ずつ計算問題が出題されています。内容は分数・少数・整数を中心とした四則計算や逆算など、いずれも難易度は易しめであるため、必ず満点を目指したい内容となっています。
計算問題の対策としては、一度に大量の問題を解くというより、コツコツ少量の問題をこなしていく方が効果的です。計算問題のみを集めた問題集やドリルなども各出版社から発売されているので、自分の好きなものを1冊購入し、毎日3〜5 問程度のペースで進めていくと良いでしょう。その際、ただがむしゃらに解くというより、入試本番と同じように慎重に解き、解き終えた後も検算をして計算ミスを減らす努力をしましょう。
問題集別対策法
【おすすめの問題集】
四谷大塚や早稲田アカデミーなどを始めとした中学受験大手塾と同じカリキュラムで算数の学習ができるシリーズ。各学年用の教材が出版されており、レベルに合った教材を選ぶことができます。予習シリーズ6年下まで一通り理解すれば中学受験における典型問題は一通りおさえることができます。予習シリーズが終了したら過去問研究に取り組みましょう。 また各ページに数問ずつ計算問題が掲載されているため、計画的に進めていけば、計算問題対策をすることもできます。このシリーズだけで基本〜標準レベルの問題をすべて網羅できる点が魅力的です。 |
実際の過去問を解いてみよう!
桜蔭中学校の算数では、「計算」、「速さ」、「図形」、「割合と比」などが頻出です。これから、実際に出題された過去問を参考に、割合と比、速さの問題の対策方法について考えましょう。
実際の出題例1〜割合と比〜
(2020年度・第2問より抜粋)
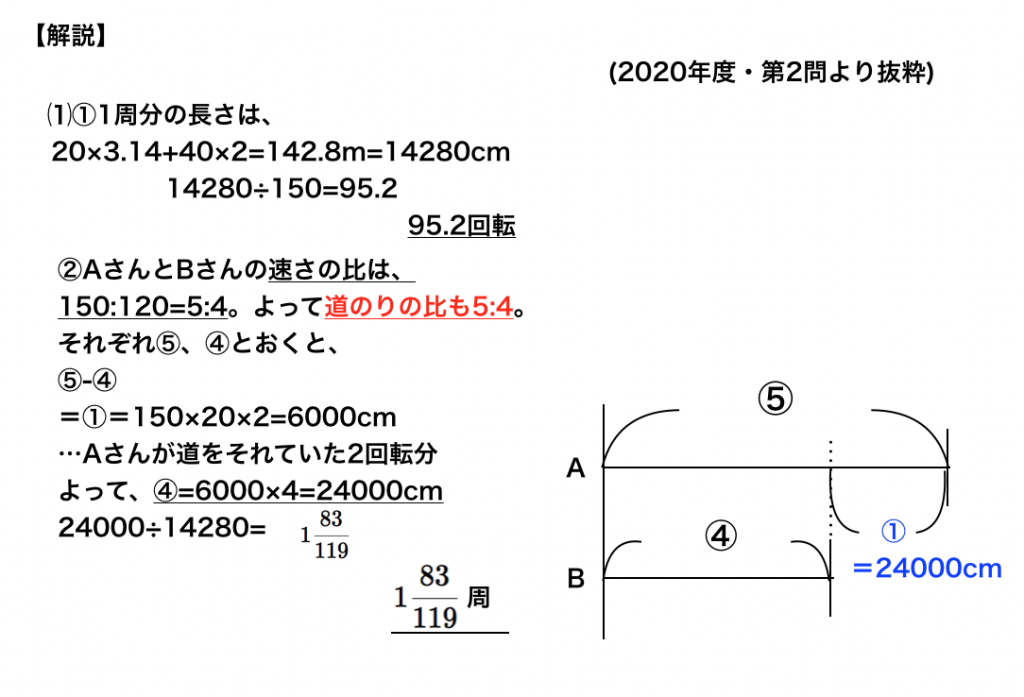
⑴右の図(本ページでは下部に記載)のようなコースで輪を転がしながら進む競走をします。コースは長方形と、半円を2つあわせた形をしています。Aさんがころがすのは州の長さ150cmの輪、Bさんがころがすのは周の長さが120cmの輪です。輪はすべることなくころがるものとします。
①Aさんがこのコースを1周すると輪は何回転しますか。
② AさんとBさんが図のスタート地点を矢印の向きに同時に出発しました。2人とも輪を1秒1回転させながら進みます。途中、Aさんは2回、輪をコースの外にころがしてしまい、コースにもどるまでに1回20秒かかりました。その後AさんとBさんは同時にゴールしました。AさんとBさんは出発してからゴールするまでにこのコースを何周しましたか。スタート地点とゴール地点は同じとは限りません。

【解答】
- ①95.2回転
- ② \(1\dfrac{83}{119}\)周
【ポイント】
- 桜蔭中学校では、前半の小問集合で「割合と比」の問題がよく出題されています。前半の問題は、基本〜標準レベルの問題がほとんどで、定型問題と同じように解くことができます。
- 難易度が比較的易しいため、満点を目指したい内容となっています。
実際の出題例2〜立体図形〜
(2017年度・第4問より抜粋)
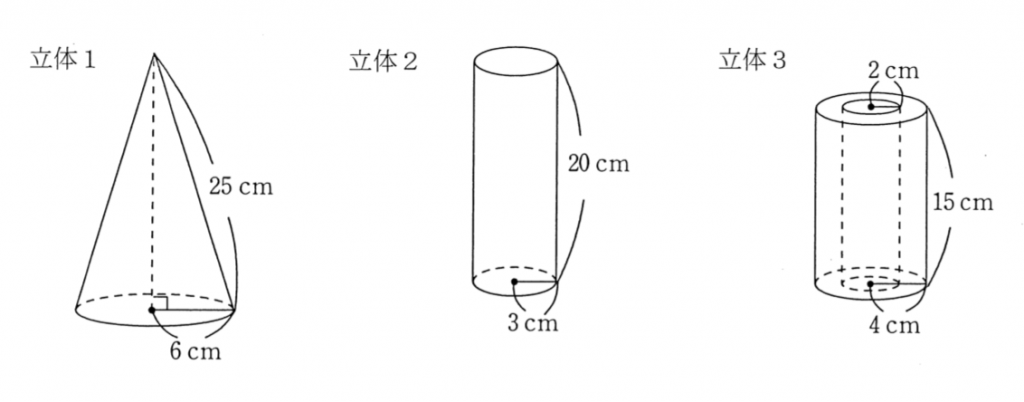
図のような立体1、2、3、がどれも1個以上あります。立体1は円すい、立体2は円柱、立体3は底面の半径が4cmの円柱から底面の半径が2cmの円柱をくりぬいてできた立体です。立体1の底面(下の面)は赤、立体2の底面(上下の2つの面)は青、立体3の底面(上下の2つの面)は黄色にぬられていて、どの立体もその他の面は全て白くぬられています。
⑴立体1、2、3の1個ずつについて、白く塗られている部分の面積と、赤、青、黄色にぬられている部分の面積をそれぞれ求めなさい。
⑵全ての立体の赤くぬられている部分の面積の合計と、青くぬられている部分の面積の合計と、黄色くぬられている部分の面積の合計がどれも同じとき、すべての立体の白く塗られている部分の面積の合計は最も少なくて何㎠ですか。
⑶全ての立体の白くぬられている部分の面積の合計が5652㎠であるとき、立体1、2、3はそれぞれ何個ずつありますか。考えられる個数の組を全て答えなさい。ただし、立体1、2、3はどれも異なる個数あるとします。解答らんは全部使うとは限りません。
【解説】
⑴
- 立体1白:25×6×3.14=471
- 立体1赤:6×6×3.14=113.04
- 立体2白:(6×3.14)×20=376.8
- 立体2青:(3×3×3.14)×2=56.52
- 立体3白:8×3.14×15+4×3×3.14×15=565.2
- 立体3黄:((4×4-2×2)×3.14)×2=75.36
⑵立体1の赤、立体2の青、立体3の黄色の面積比は、
113.04:56.5275.36=6:3:4である。これらの面積が同じとき、それぞれ2、4、3個ずつあれば良い。 ←合計が最小公倍数12になると考えて逆算する
よって、白の面積は、
(25×6×2+6×20×4+(8×15+4×15)×3)×3.14=4144.8㎠
4144.8㎠
⑶⑴より、立体1白、立体2白、立体3白の面積はそれぞれ、
150×3.14、120×3.14、180×3.14である。
5652=1800×3.14だから、立体1、2、3の個数をそれぞれA、B、Cとおくと、
150×A+120×B+180×C=1800←3.14を略して計算した方が効率的!
つまり、5×A+4×B+6×C=60
A、B 、Cがそれぞれ異なる1以上であることから、条件にあてはまる数の組み合わせは以下のようになる。
| 完成した立体の個数 | ||||
| 立体1 | 2 | 2 | 4 | 4 |
| 立体2 | 8 | 11 | 1 | 7 |
| 立体3 | 3 | 1 | 6 | 2 |
【解答】
- ⑴
- 立体1 白…471㎠ 赤…113.04㎠
- 立体2 白…376.8㎠ 青…56.52㎠
- 立体3 白…565.2㎠ 黄色…75.36㎠
- ⑵4144.8㎠
- ⑶
-
完成した立体の個数 立体1 2 2 4 4 立体2 8 11 1 7 立体3 3 1 6 2
【ポイント】
- 桜蔭中学校では、後半の応用問題で図形分野からの出題がよく見られます。今回の問題は、内容自体はそこまで難しくありませんが、全ての問題でかなりの計算量を求められます。
- 一度計算ミスをしてしまうと大幅な失点につながりかねないため、注意が必要です。「正確かつスピーディーに」問題を解くことを意識しましょう。
合格点を取るには?
前半2問でなるべく満点を目指す
桜蔭中の算数は、前半2問が計算問題・応用小問で構成されているのに対し、後半2問では応用問題が出題されています。
そのため、難易度が比較的低い前半2問でどれだけ得点できるかが、高得点を狙う上でのカギになります。全体的に基本〜標準レベルの問題が多く、定型問題が中心となっています。苦手な分野をできる限り克服し、後半の問題になるべく時間をかけられるように、「速く・正確に」解くよう意識しましょう。
また、全体的に標準〜やや難レベルと言っても、そのほとんどがややこしい計算を伴う問題となっています。大きな数や複雑な計算処理を伴う場合でもミスなくこなせるよう、日頃から計算対策はしっかり行いましょう。
過去問研究はしっかりと!
桜蔭中の算数入試では後半2問に応用問題が出題されており、他の女子校と比べてもかなり難易度が高いことが特徴的です。解法さえ分かってしまえば順調に解けるものの、一度つまずいてしまったり迷ってしまうと、答えにたどり着かないまま大幅に時間を取られてしまうような問題が多いです。
これらの問題を解くには、定型問題の対策だけでは難しい部分があるため、より実践的な力を身につける必要があります。
応用力を身につけるためには、実際に出題された過去問を研究していくことが効率的です。なるべく多くの過去問を解くことで、応用問題を解く上で必要とされる実践的な力を身につけましょう。
途中式・考え方を残すようにする
桜蔭中の算数入試では、ほとんどの問題で途中式や考え方を記述する欄が用意されています。そのため解答自体が正しくても、式や考え方についての説明が十分でなかった場合、高得点を期待することはできません。
しかし、与えらている空欄の広さも限られています。必要最低限の説明や式を整理して、コンパクトに記述することが求められます。まずは、日頃問題を解くときから途中式や考え方を整理して残すようにしましょう。一度解き終わったら自分の解答を模範解答と見比べてみて、「どのように書けばもっとコンパクトに、分かりやすく説明できるのか」といったことを考えるように意識すると良いでしょう。
時間配分は慎重に
桜蔭中の算数は、試験時間50分に対して大問数が4問、総設問数が10問前後となっています。
1問あたりにかける時間は5分程度と比較的長く感じるかもしれませんが、問題の難易度や分量を考えても、そこまで時間に余裕があるわけではありません。
時間配分の仕方についてですが、前半2問はそれぞれ5〜10分程度、後半2問はそれぞれ10〜15分程度を目安に解き進めると良いでしょう。
試験時間が始まったら、まずは自分の得意分野や解きやすそうな問題から手をつけるようにしましょう。試験終了前の5〜10分間程度は必ず見直しや検算の時間とし、計算ミスをはじめとしたケアレスミスを防ぎましょう。
総括
今回は、桜蔭中の算数入試対策についてご紹介しました。当校の算数は、前半2問が計算問題・応用小問、後半2問が応用問題という問題構成で、全体的に難易度が高めに設定されていることが特徴的です。
前半と後半の難易度を比べてみると、前半の問題には基本〜標準レベルの定型問題が多いことから、前半でどれだけ得点できるかが最終的な点差を分けると考えられます。まずは定型問題を集めた標準的なレベルの問題集を繰り返し解き、苦手な単元を克服することが重要です。定型問題を一通りマスターしたら過去問研究に移り、応用問題を解く上での実践的な力を身につけましょう。
算数は全科目の中で一番点差を分ける科目です。算数の点数が合否を分けると言っても過言ではないでしょう。入試本番まで時間は限られていますが、他科目とのバランスを考えつつ、限られた時間の中で優先順位に気をつけながら最大限の対策をしましょう。
参考
2020年桜蔭高等学校 東大・京大・難関大学 合格者数|インターエデュ
桜蔭中学校 2020年度用 10年間スーパー過去問 (声教の中学過去問シリーズ) 、声の教育社
こんにちは!ライターの福久はなです。 都内の中高一貫校出身で、大学受験を経て東京大学に入学しました。 塾講師や家庭教師のアルバイト経験があり、算数・数学・英語を中心に教えていました。 これらの科目に限らず、中学受験の経験を活かして理科・社会といった科目の対策方法や、学校別の受験対策、学校情報についてなど、幅広く記事を執筆しています。 皆さんの役に立つ、面白くてわかりやすい記事をお届けできるように頑張ります!



















