問題
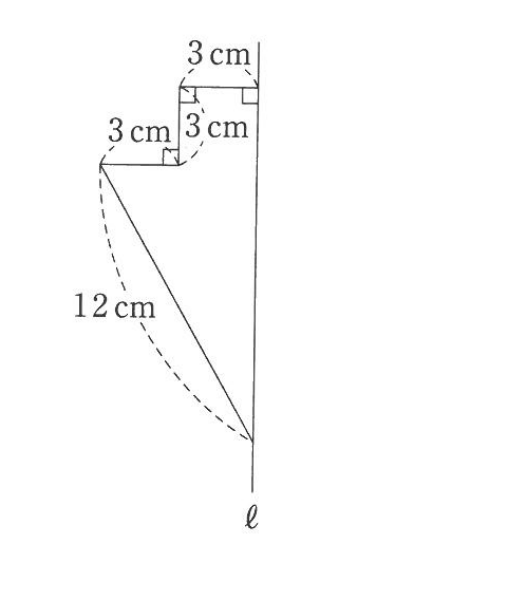
下の図形を直線ℓを軸として1回転させてできる立体の表面積は□㎠です。
解説
この図形は、半径6cmの円を底面積とする円錐とその残り部分と分解して考える事が出来ます。

まずは、円錐の表面積を求めると、
\(6 \times 6 \times 3.14+12 \times 12 \times 3.14 \times \frac{6}{12}\)
次に、円柱の側面部の面積を求めると、
\(3 \times 3 \times 2 \times 3.14\)
以上から、表面積の合計は、
\(6 \times 6 \times 3.14+12 \times 12 \times 3.14 \times \frac{6}{12}+3 \times 3 \times 2 \times 3.14\)
\(=(36+72+18) \times 3.14\)
\(=126 \times 3.14\)
\(=395.64\)
より、395.64㎠となります。
答え:□=395.64