数学Ⅰ整式の導入と具体的な計算方法について－[寝ながら学べる数学講座]

単項式と多項式

単項式…数や文字を組み合わせてできる式

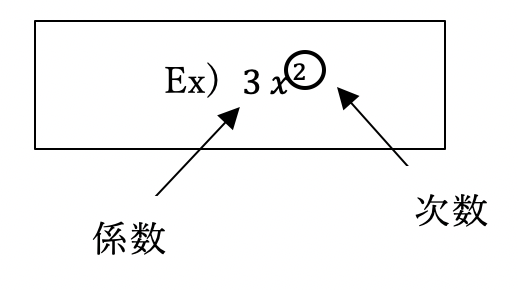
単項式の例

多項式…単項式の和で表される式

Ex) \(5ax^{3}+4x^{2}+3\)

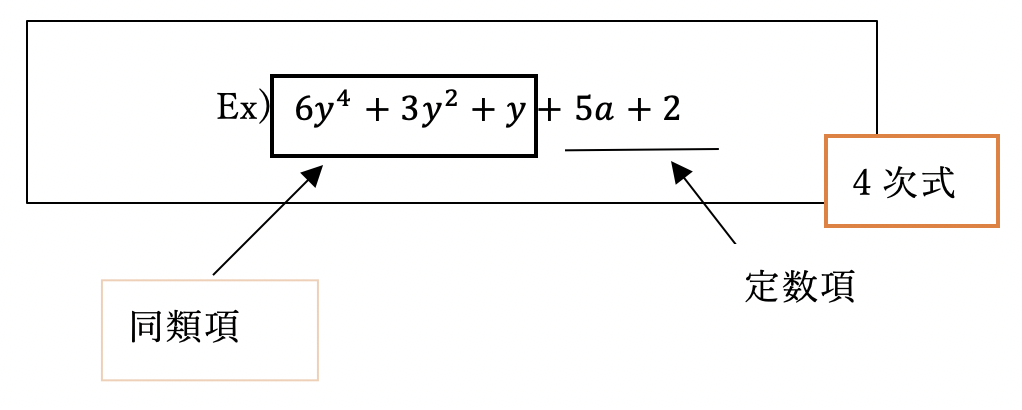
単項式と多項式を合わせて、整式と呼び、さらに、文字の種類が同じ項を同類項と呼ぶ。同類項をまとめた後、最も次数の高い項の次数を式の次数といい、その式のことをn次式という。2つ以上の文字を含む式の場合、着目しない文字を含む項をまとめて定数項という。(文字を定数とすることに若干の違和感がありますが、要は2や10などの数と同じと見做す、ということです)

また、一般に、整式は降冪の順か昇冪の順に並べることが作法とされる。

• 降冪の順…次数の高い項から順番に並べること
• 昇冪の順…次数の低い項から順番に並べること

整式における名称まとめ

演習問題

次の式の同類項をまとめて整理しなさい。また、[ ]内の文字について整理した時の次数と定数項を述べなさい。

• (1) \(5x^{2}+3x^{3}+2+4x+6x^{2}+x\)
• (2) \(4ax+3x^{2}+4+2a+5x, [x]\)
• (3) \(4ab^{3}+3a+2b^{2}+5b+6, [a], [b]\)

演習問題の解答

• (1) \(3x^{2}+11x^{2}+5x+2\)
• (2) \(3x^{2}+(4a+5)x+2a+4\)
  • 次数…\(2\)
  • 定数項…\(2a+4\)
• (3) \([a], [b]\)それぞれについて考える必要がある。
  • \([a] \cdots (4b^{3}+3)a+2b^{2}+5b+6\)
    • 次数…\(1\)
    • 定数項…\(2b^{2}+5b+6\)
  • \([b] \cdots 4ab^{3}+2b^{2}+5b+3a+6\)
    • 次数…\(3\)
    • 定数項…\(3a+6\)

整式の計算の基本法則

交換法則

• 【加法】\(X+Y=Y+X\)
• 【乗法】\(XY=YX\)

結合法則

• 【加法】\((X+Y)+Z=X+(Y+Z)\)
• 【乗法】\((XY)Z=X(YZ)\)

分配法則

• \((X+Y)Z=XZ+XY\)
• \(X(Y+Z)=XY+XZ\)

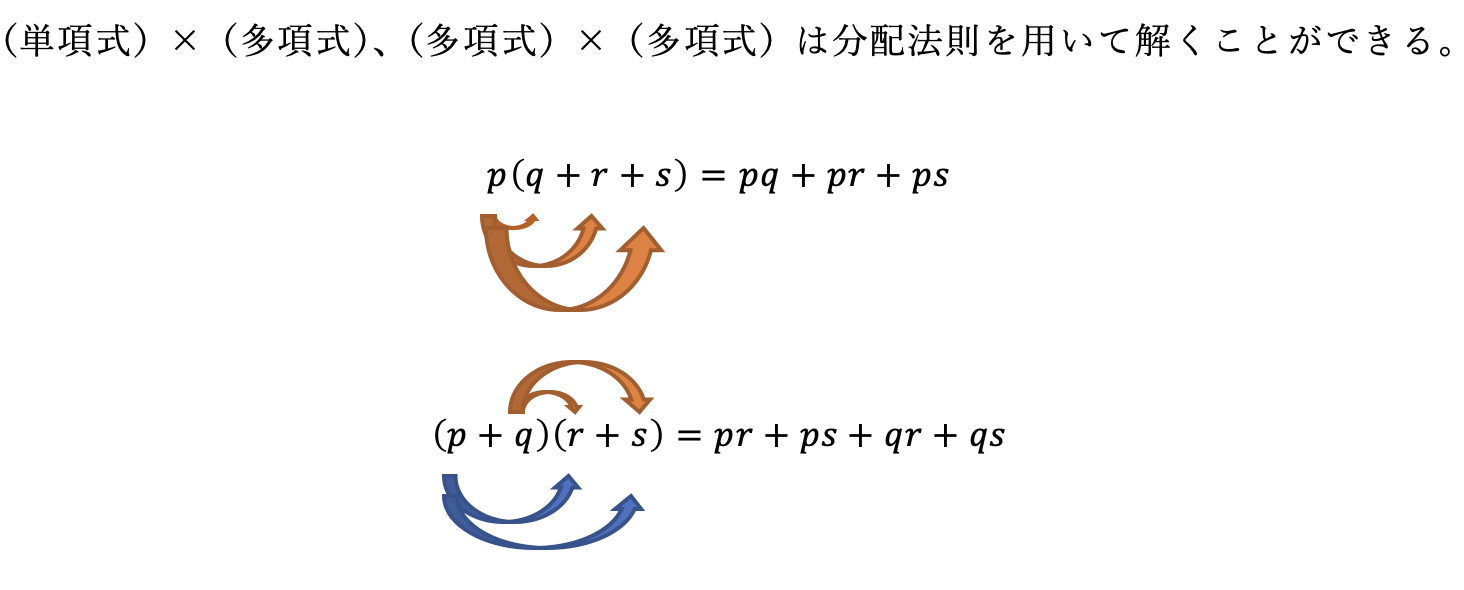
整式の計算における分配法則の例

指数法則

• \(X^{a}Y^{b}=X^{a+b}\)
  • Ex) \(x^{2}x^{4}=xx \cdot xxxx=x^{6}\)
• \((X^{a})^{b}=X^{ab}\)
  • Ex) \((a^{3})^{2}=(aaa) \cdot (aaa)=a^{6}\)
• \((XY)^{a}=X^{a}Y^{a}\)
  • Ex) \((pq)^{3}=pq \cdot pq \cdot pq=p^{3}q^{3}\)

演習問題

• 問1. \(X=a^{2}+b^{2}+3ab, Y=a^{2}-b+4ab+5, Z=-5^{2}+3b^{2}-2ab+1\)である時、以下の計算をしなさい。
  • (1) \( X+Y\)
  • (2) \(X-Z\)
  • (3) \(2X-Y+3Z\)
  • (4) \(2(Y+Z)-3X+5(X+2Z)-4Y\)
  • (5) \(\{X-Y-(Y+X)\}+2Z-3X\)
• 問2. 次の計算をしなさい。
  • (1) \((ab^{2})^{3}(-4ab)\)
  • (2) \(-xy^{3}(-5x^{2}yz)\)
  • (3) \(6xy(x^{2}-y+z^{2})\)
  • (4) \((-ab)^{2}(4a^{2}+b^{3}+3c-2)\)
• 問3. 次の式を展開しなさい。
  • (1) \((4x-3)(2x^{2}-4x+5)\)
  • (2) \((3x^{2}+x+1)(2+4x-x^{2})\)
  • (3) \((3ab+1)(a^{2}+2a-1)\)

演習問題の解説

• 問1. \(X=a^{2}+b^{2}+3ab, Y=a^{2}-b+4ab+5, Z=-5^{2}+3b^{2}-2ab+1\)である時、以下の計算をしなさい。
  • (1) \(X+Y\)
    • =\((a^{2}+b^{2}+3ab)+(a^{2}-b+4ab+5)\)
    • =\(2a^{2}+7ab+b^{2}-b+5\)
  • (2) \(X-Z\)
    • =\((a^{2}+b^{2}+3ab)-(-5^{2}+3b^{2}-2ab+1)\)
    • =\(7a^{2}+5ab-2b^{2}-1\)
  • (3) \(2X-Y+3Z\)
    • =\(2(a^{2}+b^{2}+3ab)-(a^{2}-b+4ab+5)+3(-5^{2}+3b^{2}-2ab+1)\)
    • =\(2a^{2}+2b^{2}+6ab-a^{2}+b-4ab-5-15a^{2}+9b^{2}-6ab+3\)
    • =\(-14a^{2}-4ab+11b^{2}+b-2\)
  • (4) \(2(Y+Z)-3X+5(X+2Z)-4Y\)
    • =\(2Y+2Z-3X+5X+10Z-4Y\)
    • =\(2X-2Y+12Z\)
    • =\(2(a^{2}+b^{2}+3ab)-2(a^{2}-b+4ab+5)+12(-5^{2}+3b^{2}-2ab+1)\)
    • =\(2a^{2}+2b^{2}+6ab-2a^{2}+2b-8ab-10-60a^{2}+36b^{2}-24ab+12\)
    • =\(-60a^{2}-26ab+38b^{2}+2b+2\)
  • (5) \(\{X-Y-(Y+X)\}+2Z-3X\)
    • =\(-4X+Z\)
    • =\(-4(a^{2}+b^{2}+3ab)+(-5^{2}+3b^{2}-2ab+1)\)
    • =\(-4a^{2}-4b^{2}-12ab-5a^{2}+3b^{2}-2ab+1\)
    • =\(-9a^{2}-14ab-b^{2}+1\)
• 問2. 次の計算をしなさい。
  • (1) \((ab^{2})^{3}(-4ab)\)
    • =\(-4a^{4}b^{7}\)
  • (2) \(-xy^{3}(-5x^{2}yz)\)
    • =\(5x^{3}y^{4}z\)
  • (3) \(6xy(x^{2}-y+z^{2})\)
    • =\(6x^{3}y-6xy^{2}+6xyz^{2}\)
  • (4) \((-ab)^{2}(4a^{2}+b^{3}+3c-2)\)
    • =\(4a^{4}b+a^{2}b^{5}+3a^{2}b^{2}c-2a^{2}b^{2}\)
• 問3. 次の式を展開しなさい。
  • (1) \((4x-3)(2x^{2}-4x+5)\)
    • =\(8x^{3}-16x^{2}+20x-6x^{2}+12x-15\)
    • =\(8x^{3}-22x^{2}+32x-15\)
  • (2) \((3x^{2}+x+1)(2+4x-x^{2})\)
    • =\(6x^{2}+12x^{3}-3x^{4}+2x+4x^{2}-x^{3}+2+4x-x^{2}\)
    • =\(-3x^{4}+11x^{3}+9x^{2}+6x+2\)
  • (3) \((3ab+1)(a^{2}+2a-1)\)
    • =\(3a^{3}b+6a^2b+a^{2}-3ab+2a-1\)

整式の展開

2次式の展開

• ①\((p+q)^{2}=p^{2}+2pq+q^{2}\)
• ②\((p-q)^{2}=p^{2}-2pq+q^{2}\)
• ③\((p+q)(p-q)=p^{2}-q^{2}\)
• ④\((x+p)(x+q)=x^{2}+(p+q)x+pq\)
• ⑤\((px+q)(rx+s)=prx^{2}+(ps+qr)x+qs\)

⑤は分配法則を用いて解くことができる。

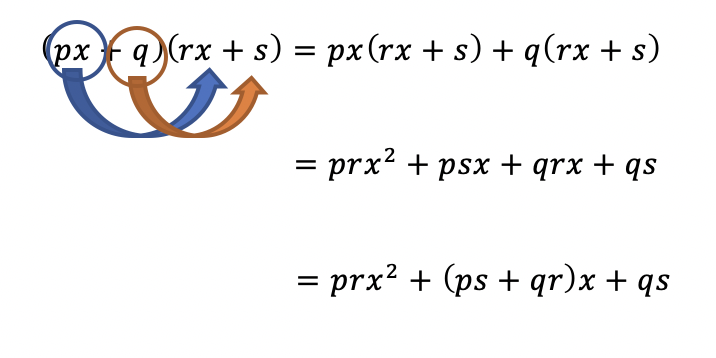
展開公式の証明

3次式の展開

• ①\((p+q)(p^{2}-pq+q^{2})=p^{3}+q^{3}\)
• ②\((p-q)(p^{2}+pq+q^{2})=p^{3}-q^{3}\)
• ③\((p+q)^{3}=p^{3}+3p^{2}q+3pq^{2}+q^{3}\)
• ④\((p-q)^{3}=p^{3}-3p^{2}q+3pq^{2}-q^{3}\)

以下で、①と③を解いてみる。

展開公式の証明その2

どちらも分配法則を使うことで、証明することができた。

2次式、3次式の展開の公式は、公式を丸暗記するのではなく、自分で解けるようにする必要がある。

演習問題

• 問1. 以下の式を展開しなさい。
  • (1)\((x+6)^{2}\)
  • (2)\((2a+3b)^{2}\)
  • (3)\((3p+5q)(3p-5q)\)
  • (4)\((x+2)(x+7)\)
  • (5)\((3p+2)(2p-4)\)
  • (6)\((4a+2b)(3a+5b)\)
• 問2. 以下の式を展開しなさい。
  
  • (1)\((a+5)(a^{2}-5a+25)\)
  • (2)\((2x-y)(4x^{2}+2xy+y^{2})\)
  • (3)\((p+7)^{3}\)
  • (4)\((3a-2b)^{3}\)

演習問題の解説

• 問1. 以下の式を展開しなさい。
  • (1)\((x+6)^{2}\)
    • =\(x^{2}+12x+36\)
  • (2)\((2a+3b)^{2}\)
    • =\(4a^{2}+12ab+9b^{2}\)
  • (3)\((3p+5q)(3p-5q)\)
    • =\(9p^{2}-25q^{2}\)
  • (4)\((x+2)(x+7)\)
    • =\(x^{2}+(2+7)x+2 \cdot 7\)
    • =\(x^{2}+9x+14\)
  • (5)\((3p+2)(2p-4)\)
    • =\(3 \cdot 2p^{2}+(-4 \cdot 3+2 \cdot 2)p+2 \cdot (-4)\)
    • =\(6p^{2}-8p-8\)
  • (6)\((4a+2b)(3a+5b)\)
    • =\(4 \cdot 3a^{2}+(4 \cdot 5+2 \cdot 3)ab+2 \cdot 5b^{2}\)
    • =\(12a^{2}+26ab+10b^{2}\)
• 問2. 以下の式を展開しなさい。
  
  • (1)\((a+5)(a^{2}-5a+25)\)
    • =\(a^{3}+125\)
  • (2)\((2x-y)(4x^{2}+2xy+y^{2})\)
    • =\(8x^{3}-y^{3}\)
  • (3)\((p+7)^{3}\)
    • =\(p^{3}+3 \cdot p^{2} \cdot 7+3 \cdot p \cdot 7^{2}+7^{3}\)
    • =\(p^{3}+21p^{2}+147p+343\)
  • (4)\((3a-2b)^{3}\)
    • =\((3a)^{3}-3 \cdot (3a)^{2} \cdot 2b+3 \cdot 3a \cdot (-2b)^{2}+(-2b)^{3}\)
    • =\(27a^{3}-54a^{2}b+36ab^{2}-8b^{3}\)

おすすめ記事

• 数学嫌い・苦手意識を克服！つまずきポイント別の勉強法をご紹介します！
• わり算が早くできるようになる！約数を見つけるコツをご紹介します！
• [例題&演習問題付き]基礎からわかりやすく！因数分解の解き方と勉強法
• [例題&演習問題付き]公式では解けない！因数分解の4つの対処法をご紹介します！
• 数学Ⅰ因数分解の導入と具体的な計算方法について－[寝ながら学べる数学講座]

参考

• チャート式参考書 | 学校採用書籍 | 数学 | 高校 – 数研出版