1.数と式(因数分解・因数定理)〜基礎から1文字整理の因数分解までマスターしよう〜[数学1]

始めに

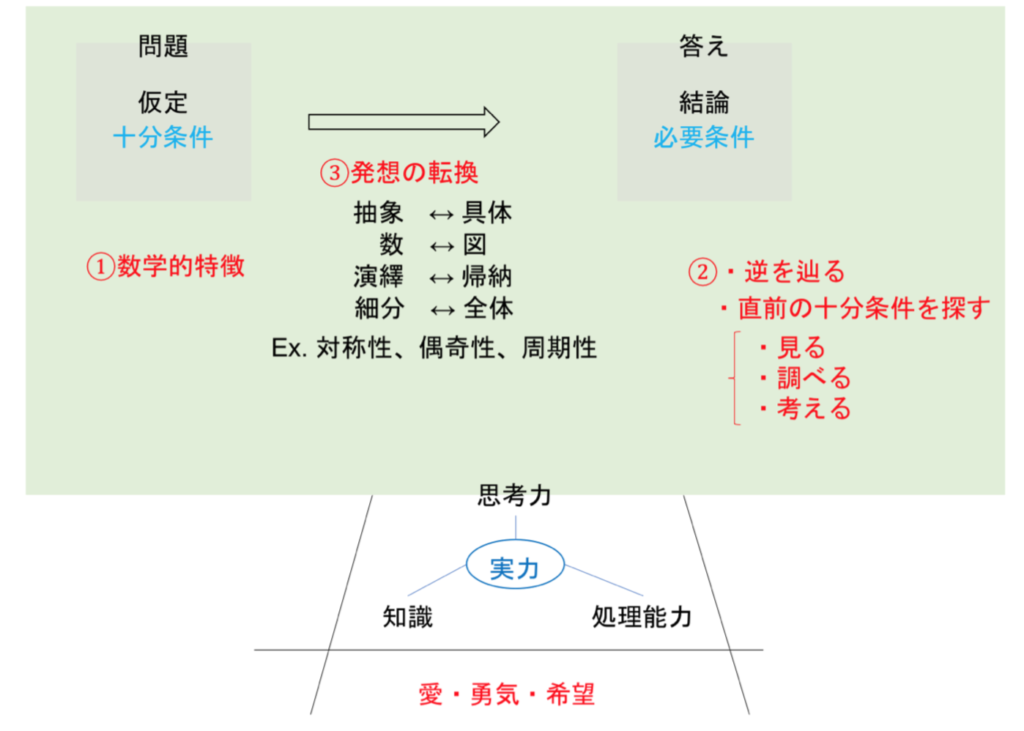
図1 始めに

因数分解

基本

【例題】

1. \(x^{2}+(a+b)x+ab\)
2. \(x^{2}-a^{2}\)
3. \(x^{2}+2ax+a^{2}\)

【解答】

1.  

   \(x^{2}+(a+b)x+ab=x^{2}+ax+bx+ab\)

   \(=x(x+a)+b(x+a)\)

   \(A=x+a\)と置くと、…置換

   \(=xA+bA\)

   \(=A(x+b)\)

   ここで\(A\)を戻すと

   \(=(x+a)(x+b)\)
   
   

2.  

   \(x^{2}-a^{2}=x^{2}-ax+ax-a^{2}\)

   0となるように項を増やす…帳尻合わせ

   \(=x(x-a)+a(x-a)\)

   \(=(x-a)(x+a)\)

3.  

   \(x^{2}+2ax+a^{2}=x^{2}+ax+ax+a^{2}\)

   \(=x(x+a)+a(x+a)\)

   \(=(x+a)(x+a)\)

   \(=(x+a)^{2}\)

【解法の手順】

step1：定数項の絶対値と因数分解
step2：定数項が、正→和、負→差を考える
step3：1次係数の絶対値に等しいものを選択
step4：1次係数の符号を等しくなるように符号をつける
step5：共通因数で括る

たすき掛け

図2 たすき掛け

【解法の手順】

step1：2次係数と定数項の絶対値を因数分解
step2：たすきに掛ける
step3：定数項が、正→和、負→差を考える
step4：1次係数の絶対値に等しいものを選択
step5：1次係数の符号と等しくなるように符号をつける
step6：共通因数で括る

• Ex.

  \(3x^{2}-14x+8=3x^{2}+12x-2x+8\) \(=3x(x-4)-2(x-4)\) \(=(x-4)(3x-2)\)

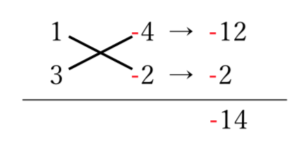
図3 たすき掛け Ex.

【裏技】

step1：\(ax^2+bx+c=0\)→積\(ac\)、和\(b\)の組を探す
step2：\(a\)との比を考える
step3：共通因数で括る

• Ex.  

  \( 3x^{2}-14x+8\)

  積24、和-14

  \(=(x-4)(3x-2)\)

証明)

\(ax^{2}+bx+c=\frac{a}{a}(ax^{2}+bx+c)\)

\(\frac{1}{a}[(ax)^{2}+b(ax)+ac]\)

 \(ax=A\)で置換すると、

\(=\frac{1}{a}[(A)^{2}+bA+ac]\)

\(α+β=b、αβ=ac\)で因数分解すると、

\(=\frac{1}{a}(A+α)(A+β)\)

\(=\frac{(ax+α)(ax+β)}{a}\)

必要があれば約分する

3乗・3元の公式

• ①\((a±b)^{n}\)

ⅰ.\(n=2\) \((a+b)(a+b)\)

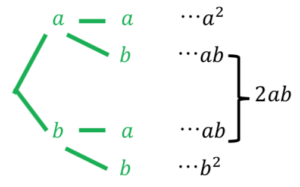
図4 (a+b)の2乗　組み合わせ

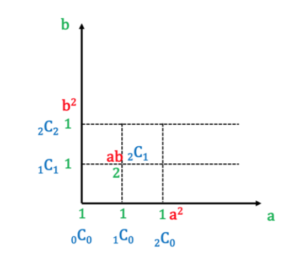
図5 (a+b)の2乗　考え方(グラフ)

ⅱ.\(n=3\) \((a+b)(a+b)(a+b)\)

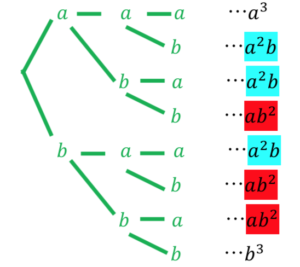
図6 (a+b)の3乗　組み合わせ

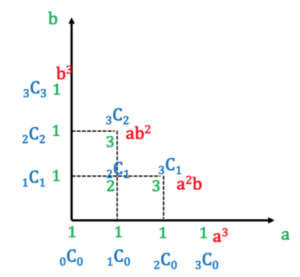
図7 (a+b)の3乗　考え方(グラフ)

\(a\)について降べき、\(b\)について昇べきの順に並べる

\((-b)\)の時は奇数乗の項に-(マイナス)がつく

【パスカルの三角形】

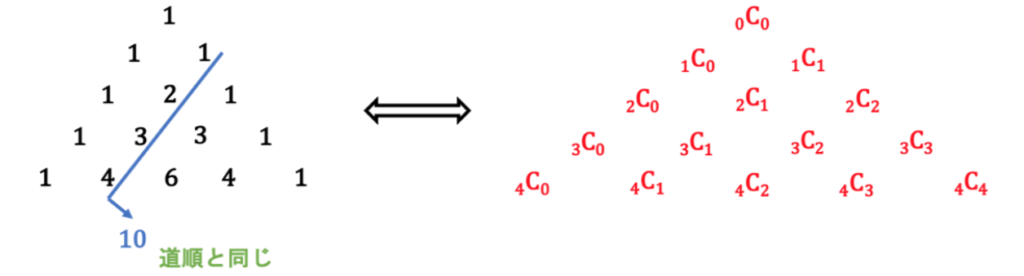
図8 パスカルの三角形

\(\sum ^{n}_{k=1}{}_k C_1 = {}_{n+1} C_2 = \frac{n(n+1)}{2}\)

\({}_n C_k + {}_n C_{k+1} ={}_{n+1} C_{k+1}\)

\((a+b)^{n}={}_n C_0 a^{n}b^{0} + {}_n C_1 a^{n-1}b^{1} + {}_n C_2 a^{n-2}b^{2} + … + {}_n C_{n-1} a^{1}b^{n-1} + {}_n C_n a^{0}b^{n}\)

・\(a^{n-k}b^{k}\)の係数 :\({}_n C_k \)

・\((a+b)^{n} = \sum ^{n}_{k=0} {}_n C_k a^{n-k}b^k\)

cf.)\(\prod ^{n}_{k=1} ak = a_{1}\times a_{2}\times … \times a_{n-1}\times a_{n}\)

Ex.\((a+b)^3 = a^3 -3a^{2}b +3ab^{b} -b^{3}\)の証明

\(a^3 -3a^{2}b +3ab^{2} -b^{3}\)

\(=a^3 -a^{2}b-2a^{2}b+2ab^{2}+ab^{2}-b^{3}\)

\(=a^{2}(a-b)-2ab(a-b)+b^{2}(a-b)\)

\(=(a-b)(a^{2}-2ab+b^{2})\)

\(=(a-b)(a-b)^2\)…\(n=2\)の公式を参照

\(=(a-b)^3\)

• ②\(a^3±b^3=(a±b)(a^2∓ab+b^2)\)

Ex. \(a^3-b^3=(a-b)(a^2+ab+b^2)\)の証明

\(a^3-b^3=a^3-a^{2}b+a^{2}b-ab^{2}+ab^{2}-b^{3}\)

\(=a^{2}(a-b)+ab(a-b)+b^{2}(a-b)\)

\(=(a-b)(a^{2}+ab+b^{2})\)

• ③\((a+b+c)^2 = a^2+b^2+c^2+2(ab+bc+ca)\)

→各々の2乗と積の2倍

• ④\(a^3+b^3+c^3-3abc=(a+b+c)(a^2+b^2+c^2-ab-bc-ca)\)

1文字整理の因数分解

【解法の手順】

step1：最小次数の文字について降べきの順に整理
step2：定数にあたる部分を因数分解
step3：共通因数を見つけるor置換する
step4：公式の形にする

• Ex.

… \(x\)の次数は3次、\(y\)の次数は2次　→\(y\)で整理

\(=-(x-1)y^2+(x-1)y+x^3-x\)

因数分解できないか考える

\(=-(x-1)y^2+(x-1)y+x(x^2-1)\)

\(=-(x-1)y^2+(x-1)y+x(x+1)(x-1)\)

\(=-(x-1)[y^2-y-x(x+1)]\)

たすき掛けを使う

\(=-(x-1)(y+x)(y-x-1)\)

\(=(x-1)(x+y)(x-y+1)\)

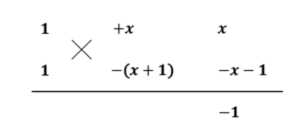
図9 1文字整理の因数分解　Ex.

因数定理

剰余の関係

• Ex.

→\(17-5-5-5=2\)…17から5が3回引けて2が余る。

これを一般化すると、

多項式の除法

• Ex.

同様に、

但し、\(0≦P\left( x\right)の次数<R\left( x\right)の次数\)

• ①筆算

Ex.\((x^3-3x+4)\div(x^2+2x-5)\)

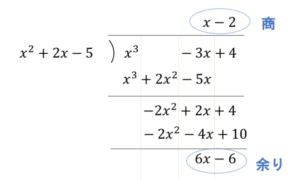
図 10 多項式の除法(筆算)

• ②組立除法(1次)

【解法の手順】

step1：割られる式の係数を書く
step2：割る式=0 となるを右上に書く
step3：左端をそのまま降ろす
step4：右上に倍して上げる
step5：足す
step6：step4、5を繰り返す

Ex.\((x^2+5x+6)\div(x+2)\)

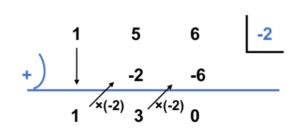
図 11 組立除法 Ex.

Ex2. \((3x^3-5x^2-11x-10)\div(3x+1)\)

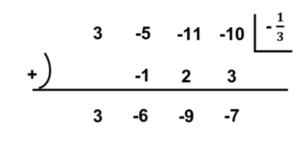
図 12 組立除法 Ex2.

• ③組立除法(2次)

Ex.\((x^3+3x^2+x+2)\div(x^2+2x-3)\)

図 13 組立除法(2次)

おすすめ記事

• 数学Ⅰ因数分解の導入と具体的な計算方法について－[寝ながら学べる数学講座]
• [例題&演習問題付き]基礎からわかりやすく！因数分解の解き方と勉強法
• [例題&演習問題付き]公式では解けない！因数分解の4つの対処法をご紹介します！

参考

• チャート研究所、『チャート式基礎からの数学Ⅰ+A』、数研出版、2019