Contents
集合
定義
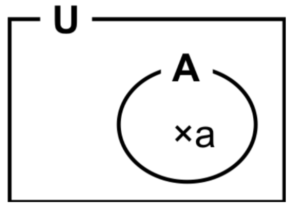
図1 集合の定義
- \(U\):全体集合
- \(A\):ある性質を持った(客観的に分けられる)物・人などの集まり
- \(a\):要素
\(a∈A\)…要素\(a\)は集合\(A\)に属する。 - \(∅\):要素のない集合(空集合)
部分集合
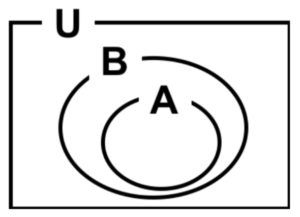
図2 部分集合
- \(A⊆B\)…\(A\)は\(B\)の部分集合
部分集合:ある集合に対して、一部の要素だけを取り出した集合。
- \(A⊂B\)…\(A\)は\(B\)の真部分集合
真部分集合 : 部分集合の内、元の集合とは一致しない集合。
\(A\)と\(B\)が一致する場合は\(A=B\)、\(∅⊂A\)
\(A⊆B⇔x∈A⇒x∈B\)
(\(A\)の任意の要素\(x\)が\(B\)の要素である)
論理和(OR)・論理積(AND)・否定(NOT)
- ①論理和(和集合)
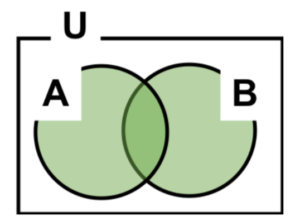
図3 論理和
\(A∪B\)
\(A OR B\)
- ②論理積(積集合)
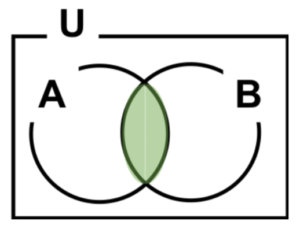
図4 論理積
\(A∩B\)
\(A AND B\)
- ③否定(補集合)
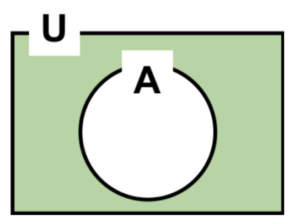
図5 否定
\(\overline{A}\)
\(NoT A\)
\(\overline{\overline{A}}⇔A\)
\(\overline{∅}⇔U\)
\(\overline{U}⇔∅\)
\(A∩\overline{A}⇔∅\)
\(A∪\overline{A}⇔U\)
※真偽表 真 ; T…1 / 偽 ; F…0
| \(A\) | \(B\) | \(A∪B\) | \(A∩B\) |
|
0 |
0 |
0 |
0 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
1 |
ド・モルガンの定理
- \(\overline{A∪B}=\overline{A}∩\overline{B}\)
- \(\overline{A∩B}=\overline{A}∪\overline{B}\)
否定をとると AND OR が入れ換わる
証明)
- ①
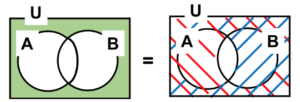
図 6 ド・モルガンの定理①
\(\overline{A∪B}=\overline{A}∩\overline{B}\)
- ②
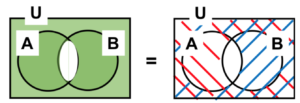
図 7 ド・モルガンの定理②
\(\overline{A∩B}=\overline{A}∪\overline{B}\)
※\(A∩(B∪C)⇔(A∩B)∪(A∩C)\)…分配則
(\(∩:\times\)、\(∪:+\))
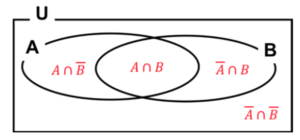
図8 分配則
否定をとって論理積を作る!!
- Ex.\((A∩\overline{B})∪(A∩B)=A∩(B∪\overline{B})=A∩U=A\)
- Ex2.
\((A∩\overline{B})∪(A∩B)∪(\overline{A}∩B)\)
\(=\overline{\overline{A∪\overline{A}∩B}}\)
\(=\overline{\overline{A}∩\overline{(\overline{A}∩B)}}\)
\(=\overline{\overline{A}∩(A∪\overline{B})}\)
\(=\overline{∅∪\overline{A}∩\overline{B}}\)
\(=\overline{(\overline{A}∩\overline{B})}\)
\(=A∪B\)
要素の個数
表を書いて整理!
- ①2集合
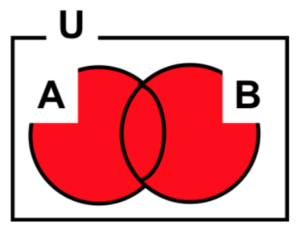
図9 2集合
\(n(A)\):\(A\)の要素の個数
\(n(A∪B)=n(A)+n(B)-n(A∩B)\)
証明)
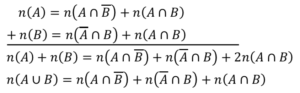
図10 2集合 証明
- ②3集合
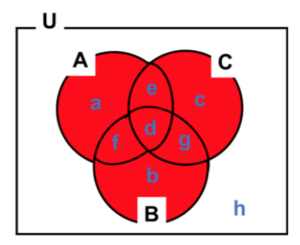
図11 3集合
\(n(A∪B∪C)=n(A)+n(B)+n(C)-n(A∩B)-n(B∩C)-n(C∩A)+n(A∩B∩C)\)
証明)
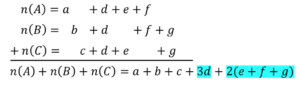
図12 3集合 証明①
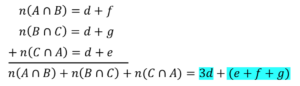
図13 3集合 証明②
論理
命題
命題とは
…客観的に真(T)偽(F)が判断できる文
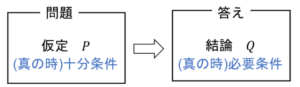
図14 命題
\(P⇒Q\)が真\(P⊆Q\)
条件の判定
【判定の手順】
step1. 同値変形
- 方程式、不等式を解く
- グラフ化する
step2. 真となるように⇒をつける
- 真にならない時は「どちらでもない」
⇔となる時は必要十分条件(同値)
step3.\(P⇒Q\) \(P\):十分条件、\(Q\):必要条件
条件の否定
…基本的には集合を同じ
- ①All 恒等式
全ての要素(\(x\))について\(P\)(条件)が成り立つ \({}^∀x{P}\)
- ②Some 解の存在
ある要素について\(P\)が成り立つ
\(⇔P\)を満たす要素が少なくとも1つ存在する \({}^∃x{P}\)\(\overline{{}^∀x{P}}⇔{}^∃x{P}\)
\(\overline{{}^∃x{P}}⇔{}^∀x{P}\)
逆・裏・対偶
\(P⇒Q\)
\(P⇐(逆)Q\)
\(\overline{P}⇒(裏)\overline{Q}\)
\(\overline{P}⇐(対偶)\overline{Q}\)
- 元の命題と対偶
- 逆の命題と裏
→真偽が一致する
| \(P⇒Q\) |
0 |
1 |
| \(P⇐Q\) |
? |
? |
| \(\overline{P}⇒\overline{Q}\) |
? |
? |
| \(\overline{P}⇐\overline{Q}\) |
0 |
1 |
証明の論法
- ①三段論法(同値)
\((A⇔B∩C⇔C)⇒A⇔B\)
Ex.
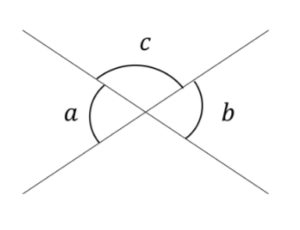
図15 三段論法 Ex.
- ②対偶を示す
\(P⇒Q\)を示すために\(\overline{P}⇒\overline{Q}\)を示す(\(Q\)が否定を含む時、論理和・論理積の時有効)
- ③背理法
\(P⇒Q\)を示すために\(P⇒\overline{Q}\)と仮定すると矛盾していることを示す (\(Q\)が二律背反である時有効)
Ex. \(\sqrt{2}\)が無理数であることの証明
\(\sqrt{2}\)を有理数と仮定すると、\(\sqrt{2}=\frac{n}{m}\)(\(m\)、\(n\)は互いに素)と書ける
\(\sqrt{2}=\frac{n}{m}\)
\(2=(\frac{n}{m})^2\)
\(2=(\frac{n^2}{m^2})\)
\(n^2=2m^2\)
より、\(n≡0(mod2)\)
\(n=2k\)とおくと、
\(4k^2=2m^2\)
\(m^2=2k^2\)
より\(m≡0(mod2)\)
これは\(m\)と\(n\)が互いに素であることに矛盾する。
故に\(\sqrt{2}\)は有理数ではない、即ち無理数である。
- ④数学的帰納法(一般項\(n\)について有効)
【証明の手順】
(ⅰ)\(n=1\)の時、\(P_{1}⇒Q_{1}\)が成立
(ⅱ)\(n=k\)の時、\(P_{k}⇒Q_{k}\)が成立すると仮定すると、
\(P_{k+1}⇒Q_{k+1}\)が成立
(ⅰ)(ⅱ)より\(∀_{n}[P_{n}⇒Q_{n}]\)
cf).
演繹 ⇔ 帰納
(ルネ・デカルト) (フランシス・ベーコン)
プラグマティズム











