今回は、「やりとり算」の解き方について解説していきます。
基本問題、応用問題と用意しているので、ご自身のレベルに合わせてぜひ参考にしてみてください。
なお、線分図の書き方や基本的な考え方は「和差算の記事」と「分配算の記事」を読むとわかりやすいので、不安な方はぜひそちらから読んでみてください。
やりとり算とは
やりとり算とは、ものをどのようにやりとりしたかが与えられ、最初の状態を問われる問題です。
やりとりの前後において全体の量が変わらないことや、やりとりの前後の変化に着目して解いていきます。
これだけだとわかりにくいので、実際に問題を見てみましょう。
A、B、Cの3人が最初にいくらかずつお金を持っていました。今、A君がB君に所持金の半分をあげ、次にB君がC君に600円あげ、最後にC君がA君に300円あげました。すると、A君、B君、C君のそれぞれの所持金は1100円、2700円、3500円となりました。A君、B君、C君はそれぞれ最初いくら持っていたでしょうか。
A、B、C、Dの4つの容器に水が入っている。最初CにはAの3倍だけの水が入っている。CからBに0.6L、CからDに1.5L移し、次にBからAに0.5L移したところ全ての容器の水の量が等しくなった。最初にそれぞれの容器にはどれだけの水が入っていたでしょうか。
これだと想像がつきやすいのではないでしょうか。
和差算や分配算は与えられた条件を線分図に書いていけば自然に答えが導かれましたが、やりとり算は最初の状態を線分図で表すことが難しいことが多いです。
ただ、やりとりの後の状態は簡単に分かることが多いので、やりとりの後の線分図を書いてから一つずつ戻していくことで最初の状態を求めることが基本となります。
やりとり算の解き方
まずは①の問題を実際に解きながら、やりとり算の解き方について解説していきます。
（問題①）A、B、Cの3人が最初にいくらかずつお金を持っていました。今、A君がB君に所持金の半分をあげ、次にB君がC君に600円あげ、最後にC君がA君に300円あげました。すると、A君、B君、C君のそれぞれの所持金は1100円、2700円、3500円となりました。A君、B君、C君はそれぞれ最初いくら持っていたでしょうか。
問題文が長いのでとっつきにくいと感じる方もいるかもしれませんが、図で表すと簡単なので、まずはなんとなく読んでみてください。
分配算や和差算ではとりあえず線分図を書いてみましたが、今回は最初の状態がわからないので正確な線分図を書くことができません。
しかし、やりとりの終わった後の状態（A君、B君、C君の所持金がそれぞれ1100円、2700円、3500円）ははっきりしているので、線分図を書くことができます。実際に図で確認してみましょう。
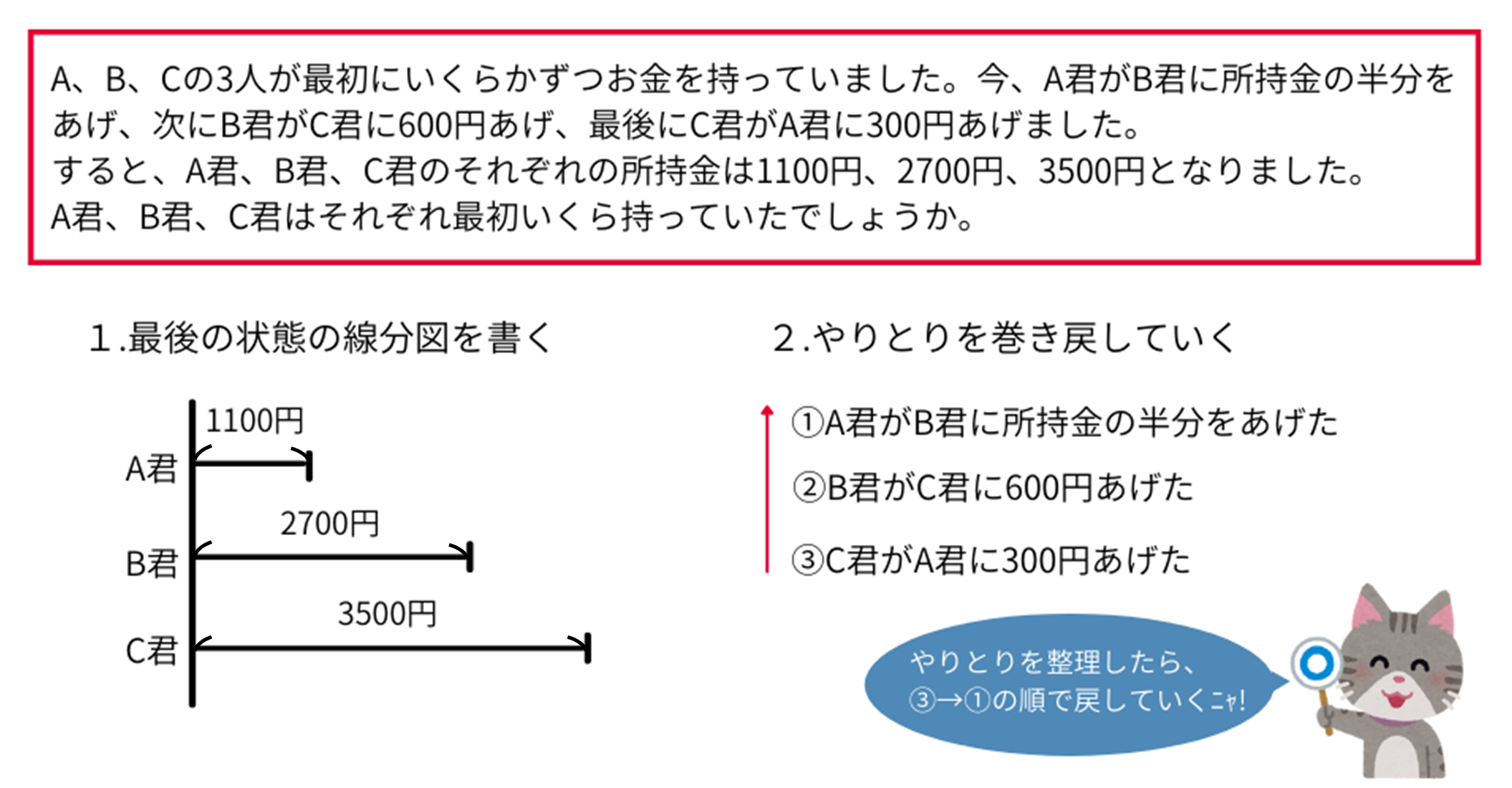
最後の状態を線分図で表すことができました。今回知りたいのは最初の状態なので、最後の状態からやりとりを巻き戻していって最初の状態にしていきます。
やりとりを巻き戻す前に1つずつ整理してみましょう。問題文に書かれた順番で並べてみると、次のようになります。
- \(A\)君が\(B\)君に所持金の半分をあげた
- \(B\)君が\(C\)君に\(600\)円あげた
- \(C\)君が\(A\)君に\(300\)円あげた
最後から最初に戻していくときは、③→②→①の順で戻していくことになります。では実際に③から戻してみましょう。
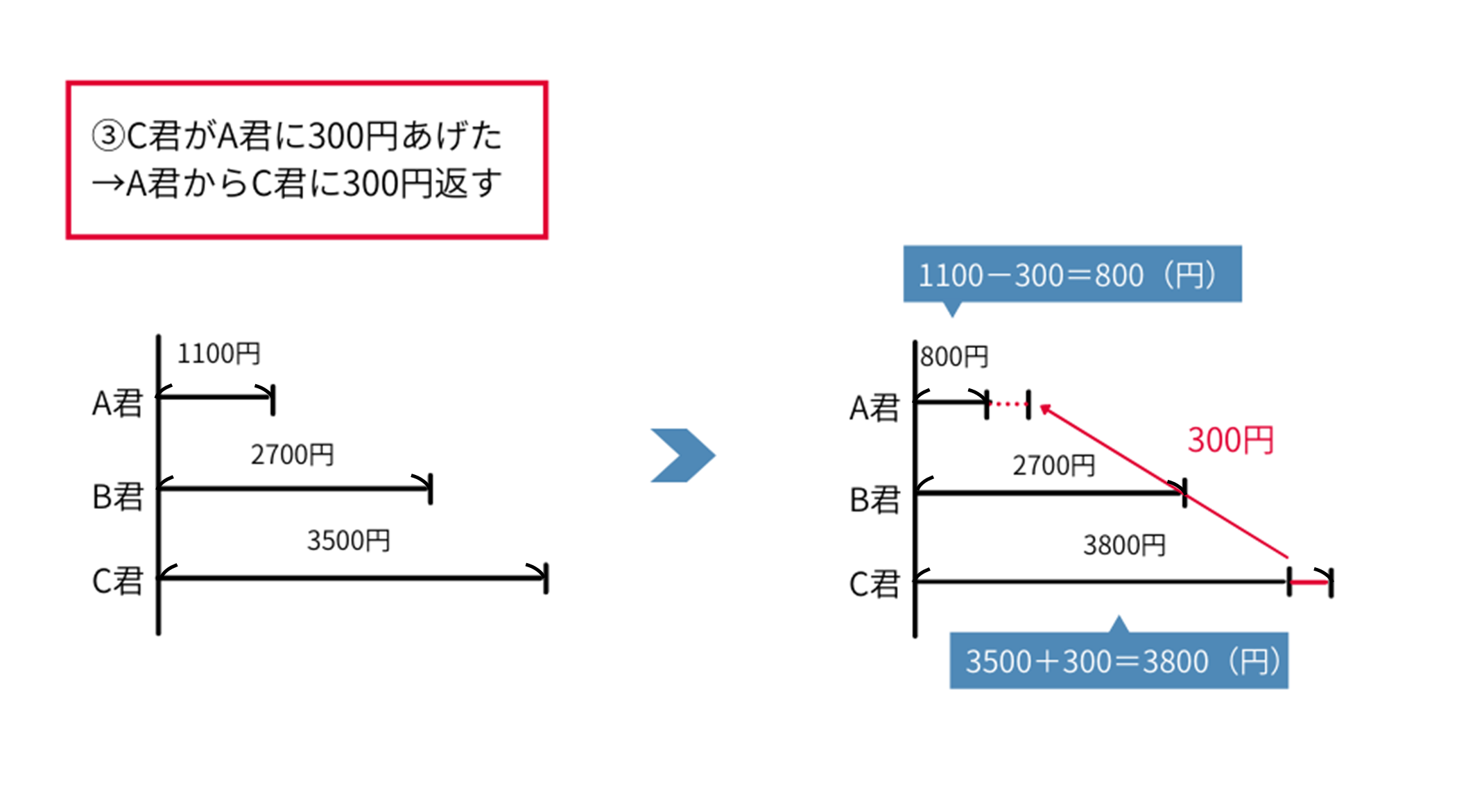
「③\(C\)君が\(A\)君に\(300\)円あげた」を元に戻すには、「\(A\)君から\(C\)君に\(300\)円返す」ことをします。
A君は\(1100－300＝800\)（円）、C君は\(3500＋300＝3800\)（円）となります。
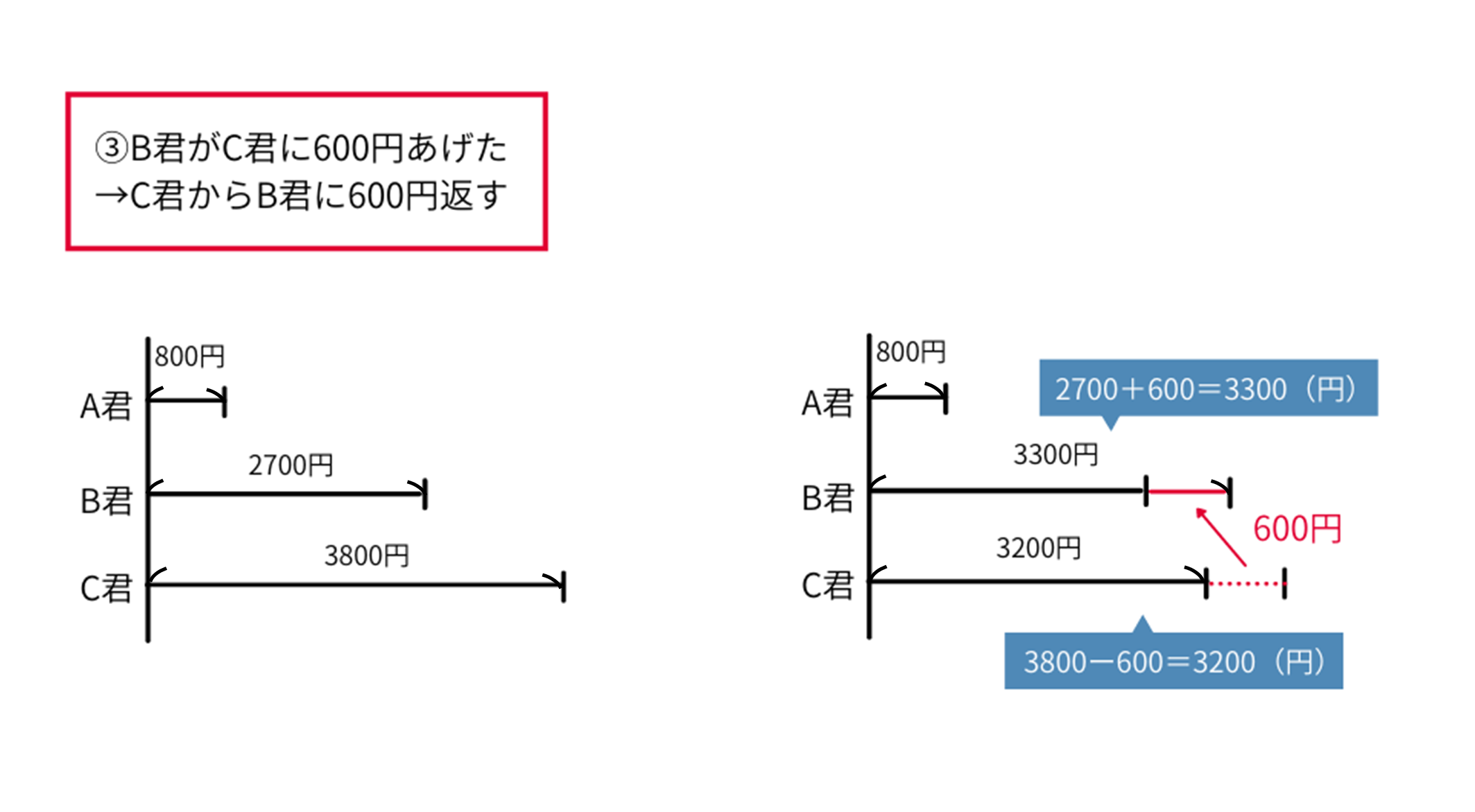
次に、②のやりとりを戻していきます。「②\(B\)君が\(C\)君に\(600\)円あげた」を元に戻すには、「\(C\)君から\(B\)君に\(600\)円返す」ことをします。
\(C\)君は\(3800－600＝3200\)（円）、\(B\)君は\(2700＋600＝3300\)（円）となります。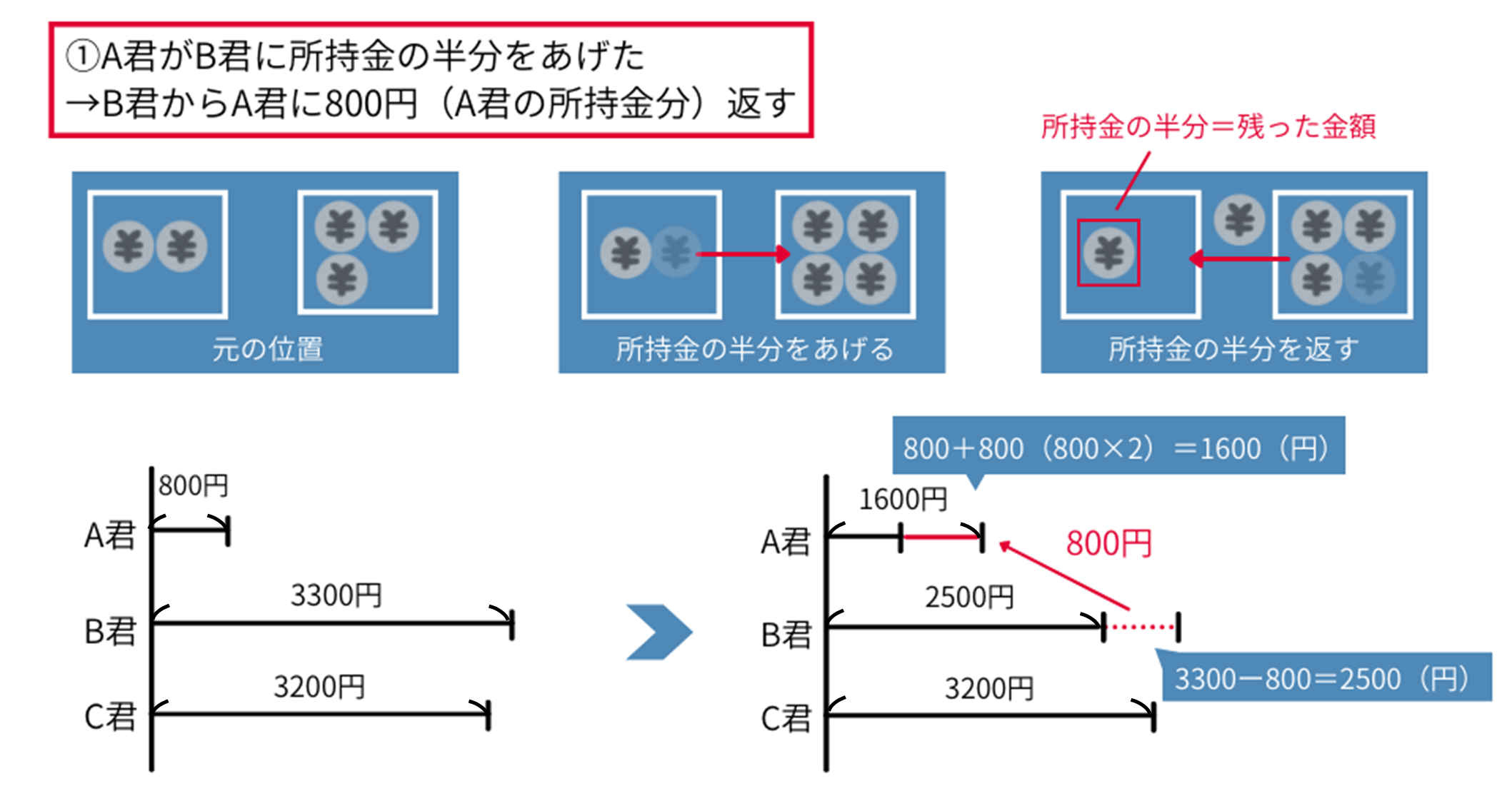
最後に、①を戻します。「①\(A\)君が\(B\)君に所持金の半分をあげた」というやりとりを元に戻すには、「\(B\)君から\(A\)君に、\(A\)君の所持金の半分を返す」必要があるのですが、ここは注意しなくてはなりません。
「\(A\)君の所持金の半分」だから、今の\(A\)君の所持金（\(800\)円）の半分で\(400\)円だ！とするのは間違いです。
「\(A\)君の所持金の半分」というのは、やりとりする前の\(A\)君の所持金の半分です。つまり、やりとりした後は\(A\)君の所持金が半分になったということです。（わからない人は図も参考にしてみてください）
\(A\)君の所持金が半分になったということは、やりとりした金額は今の\(A\)君の所持金（\(800\)円）だとわかります。 \(B\)君は\(3300－800＝2500\)（円）、\(A\)君は\(800＋800＝1600\)（円）となります。これですべてのやりとりを巻き戻せたので、これが\(A\)君、\(B\)君、\(C\)君の最初の所持金です。
よくわからなかった人や自信のない人は、問題文にそって実際にやりとりをして確認してみるといいと思います。
やりとり算の応用
次に、応用として先ほどより難しい問題を解説していきます。余裕のある人や挑戦してみたい人はぜひ解いてみてください。
（問題②）A、B、C、Dの4つの容器に水が入っている。最初CにはAの3倍だけの水が入っている。CからBに0.6L、CからDに1.5L移し、次にBからAに0.5L移したところ全ての容器の水の量が等しくなった。最初にそれぞれの容器にはどれだけの水が入っていたでしょうか。
この問題も先ほどと同じように解いていきましょう。
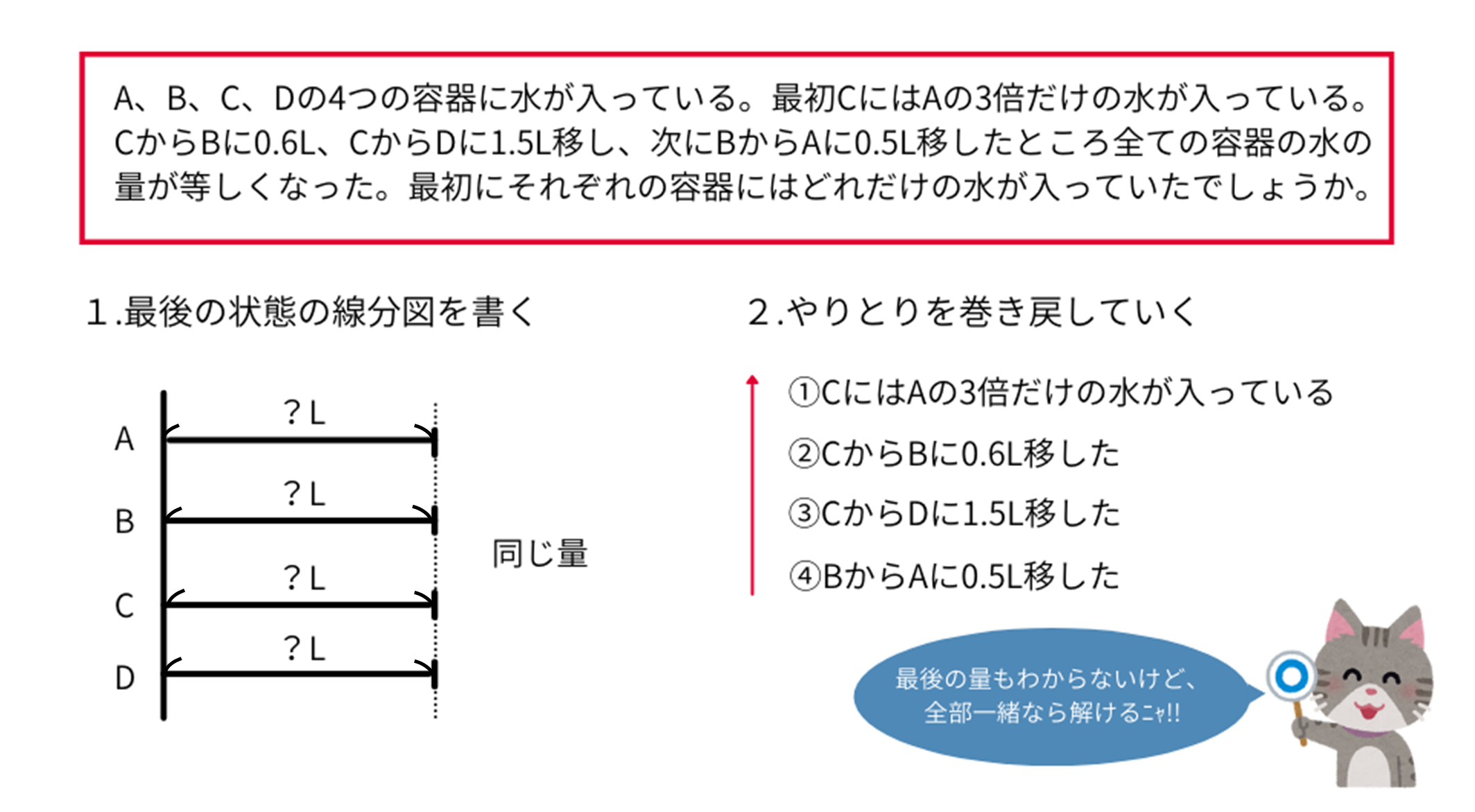
まずは最後の状態を線分図に書いていきます。今回は具体的な数字はわかりませんが、全て同じ量だと書いてあるので、それがわかるように書いてみます。
そうしたら、やりとりを整理していきます。今回も問題文の順番で並べてみると、次のようになります。
- \(C\)には\(A\)の\(3\)倍だけの水が入っている
- \(C\)から\(B\)に\(0.6L\)移した
- \(C\)から\(D\)に\(1.5L\)移した
- \(B\)から\(A\)に\(0.5L\)移した
①はやりとりではないので3つだけでもいいのですが、今回は説明しやすいように4つに分けています。ここから④→③→②→①の順で戻していきましょう。
問題B 線分図2
「④\(B\)から\(A\)に\(0.5L\)移した」を元に戻すには、「\(A\)から\(B\)に\(0.5L\)戻す」ことをします。
今回は最後の状態がわからないので、最後の状態（\(A＝B＝C＝D\)）を\(？L\)として考えていきたいと思います。
\(A\)は\(？－0.5（L）\)、\(B\)は\(？＋0.5（L）\)となります。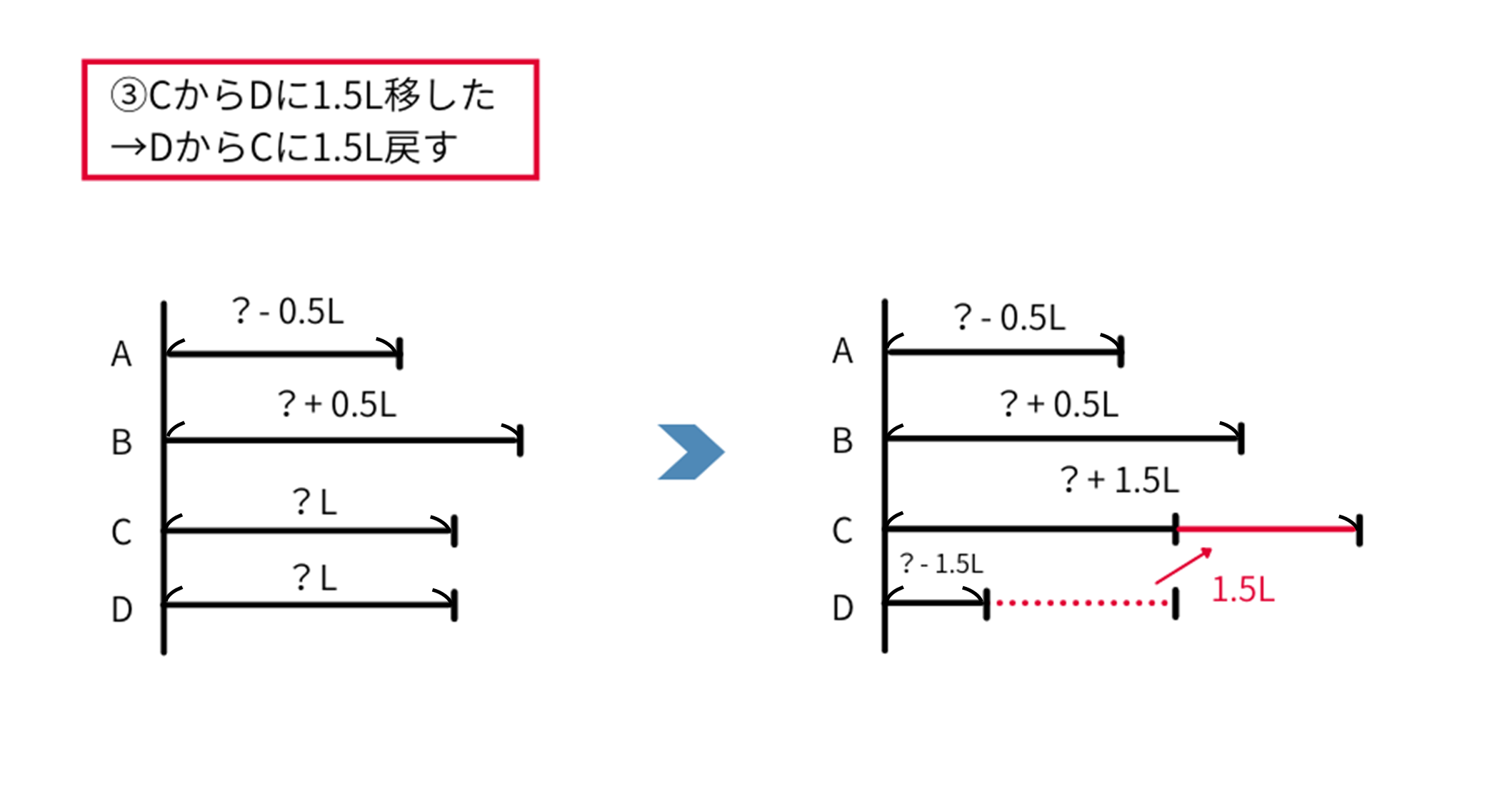
次に③を戻していきます。「③\(C\)から\(D\)に\(1.5L\)移した」を元に戻すには、「\(D\)から\(C\)に\(1.5L\)戻す」ことをします。
\(D\)は\(？－1.5（L）\)、\(C\)は\(？＋1.5（L）\)となります。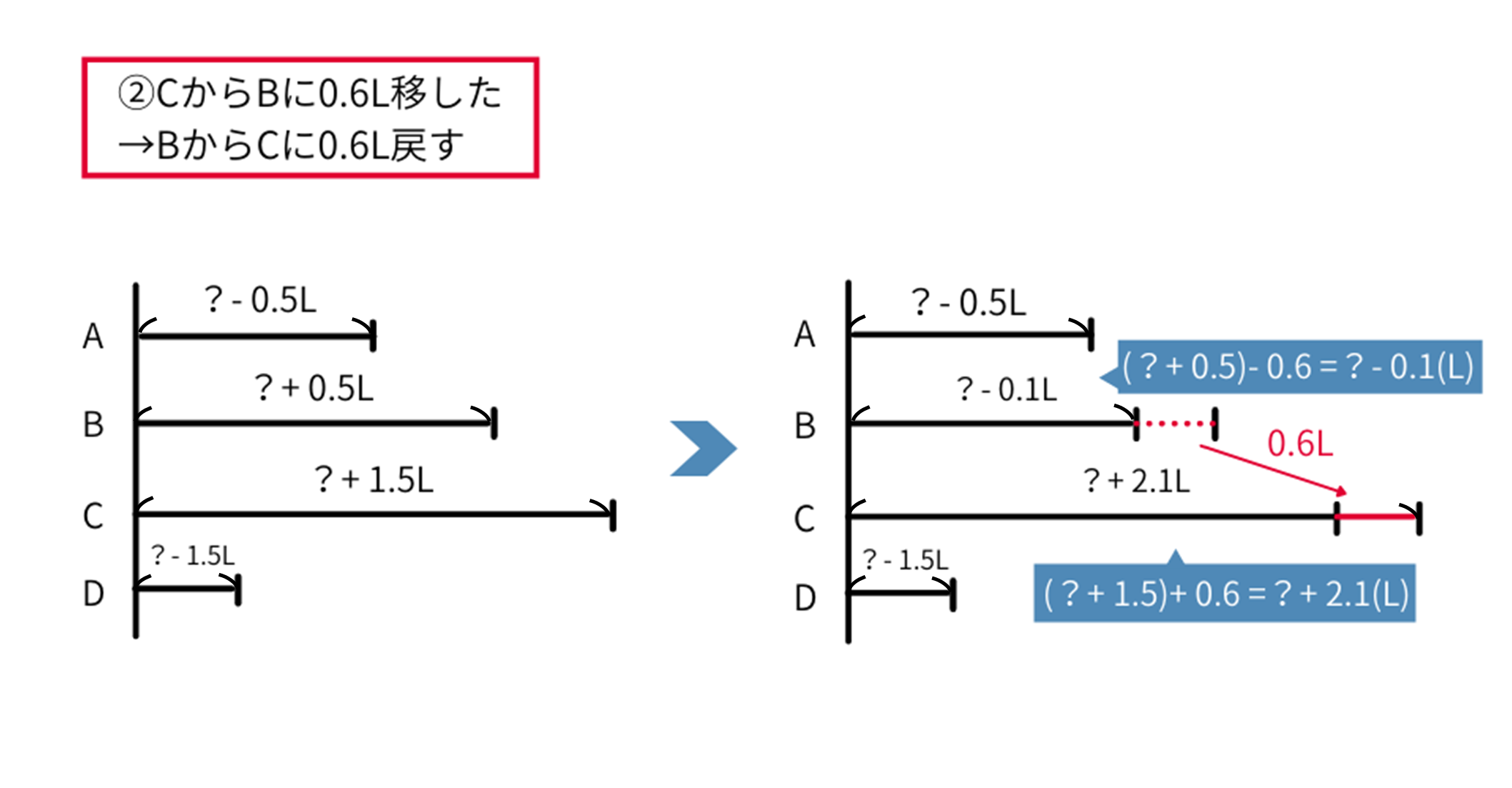
次に②を戻していきます。「②\(C\)から\(B\)に\(0.6L\)移した」を元に戻すには、「\(B\)から\(C\)に\(0.6L\)戻す」ことをします。
\(B\)は\(（？＋0.5）－0.6＝？－0.1（L）\)、\(C\)は\(（？＋1.5）＋0.6＝？＋2.1（L）\)となります。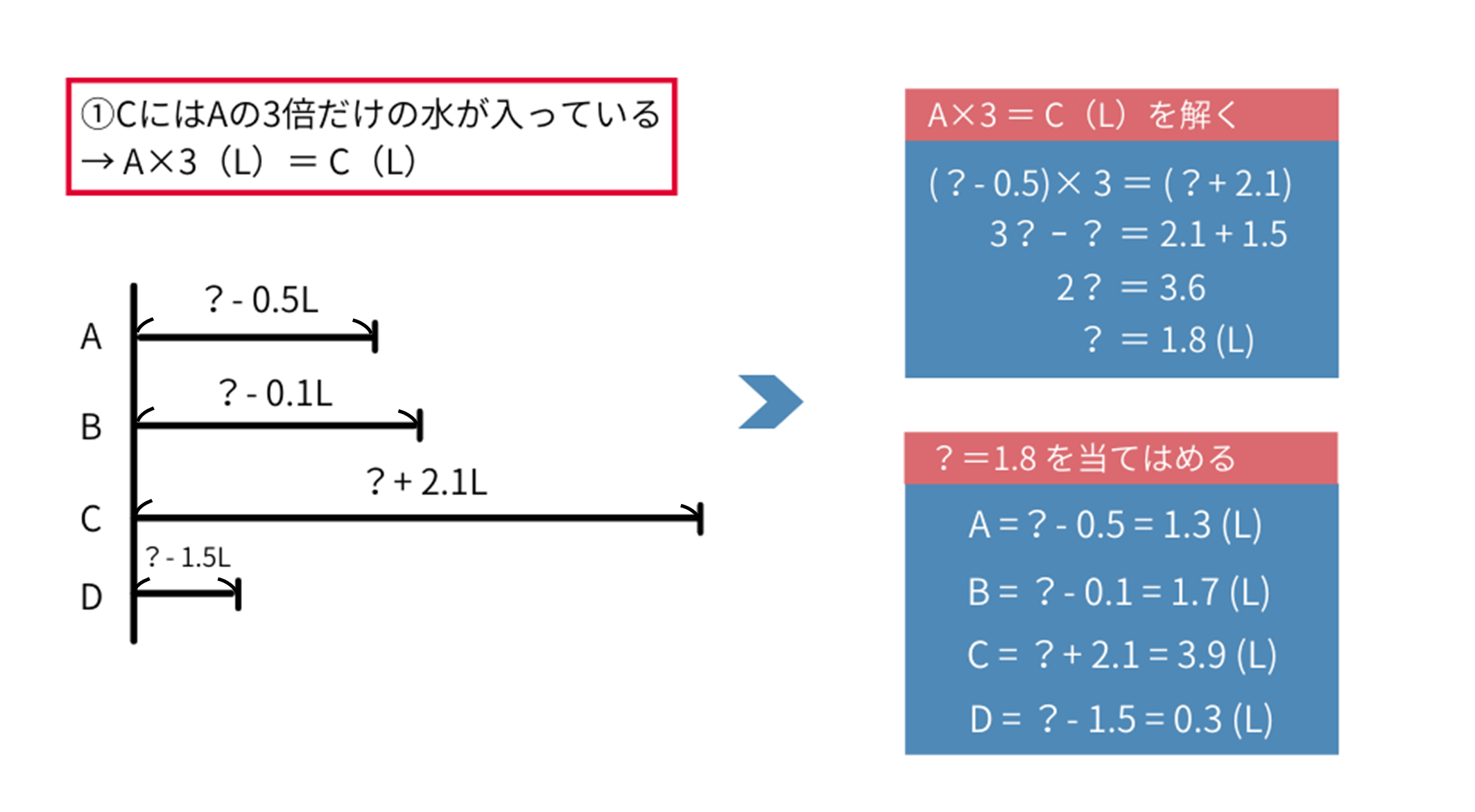
最後に①ですが、①ではやりとりしません。「①\(C\)には\(A\)の\(3\)倍だけの水が入っている」は、「\(A×3（L）＝C（L）\)」ということです。
ここで今の状態を確認すると、\(A＝？－0.5（L）\)、\(C＝？＋2.1（L）\)です。これを上の式に当てはめてみると、\(（？－0.5）×3＝（？＋2.1）\)で、\(？＝1.8（L）\)となります。
\(？＝1.8\)を当てはめると、それぞれの最初の状態がわかります。- \(A＝？－0.5＝1.3（L）\)
- \(B＝？－0.1＝1.7（L）\)
- \(C＝？＋2.1＝3.9（L）\)
- \(D＝？－1.5＝0.3（L）\)
今回は「？」という文字を置いて解いていきましたが、文字を使わずに最後の状態からの差で求めることもできます。
まとめ……の前に
登録6000人以上！ 本サイト、中学受験ナビの監修も務めている『開成番長』こと繁田和貴が執筆する完全無料のメールマガジンでは、主に中学受験生のお子さんをお持ちの方へ向けた様々なお役立ち情報を配信中！ さらに今なら登録者にはもれなく「開成番長・繁田の両親が語る繁田の中学受験PDF」をプレゼント！ 登録及び登録解除も簡単ですので、お気軽にご登録ください。
最後に
最後に、基本的なやりとり算の解き方をまとめておきます。
【やりとり算の解き方】
- 最後の状態の線分図を書く
- やりとりを整理する
- 問題文と逆の順番でやりとりを戻していく
やりとりが具体的な数字でないときは、問題文のまますぐに戻そうとせずに、やりとりの前と後を考えてみましょう。
やりとり算が苦手な人も、簡単な問題や似た問題をどんどん解いて得意になってもらえたら嬉しいです。
おすすめ記事
参考
東京大学理科二類の岡部信です。
京都の高校に通っていたので東京は知らないことだらけです。特に通勤電車はすし詰め状態だと聞いていましたが、ここまでだとは思ってなかったです。実家では犬を飼っていたのですが、もう3ヶ月近く会っていないのでそれが1番寂しいです。今は千葉で父と姉と3人暮らしですが、9月からは東京で1人暮らしする予定なので楽しみです。大学ではテニスサークルと東大村塾という農業と村おこしを掛け合わせたような活動をしているサークルに入っています。趣味は料理、登山です。料理は高校の時に料理研究部に入っていたのでそこそこ出来ますが、もっと上手くなれるよう時間がある時は夕ご飯を作ったりしてます。お菓子も色々作れるようになりたいです。登山は友達と休日に日帰りで行ったり、夏休みは泊まりで行ったりもしてます。今年の夏は富士山と北海道の富良野岳に行く予定です。
皆さんよろしくお願いします。
